2.6探索勾股定理(一)[上学期]

课件17张PPT。2.6探索勾股定理(一)一.你们已掌握直角三角形的那些性质?
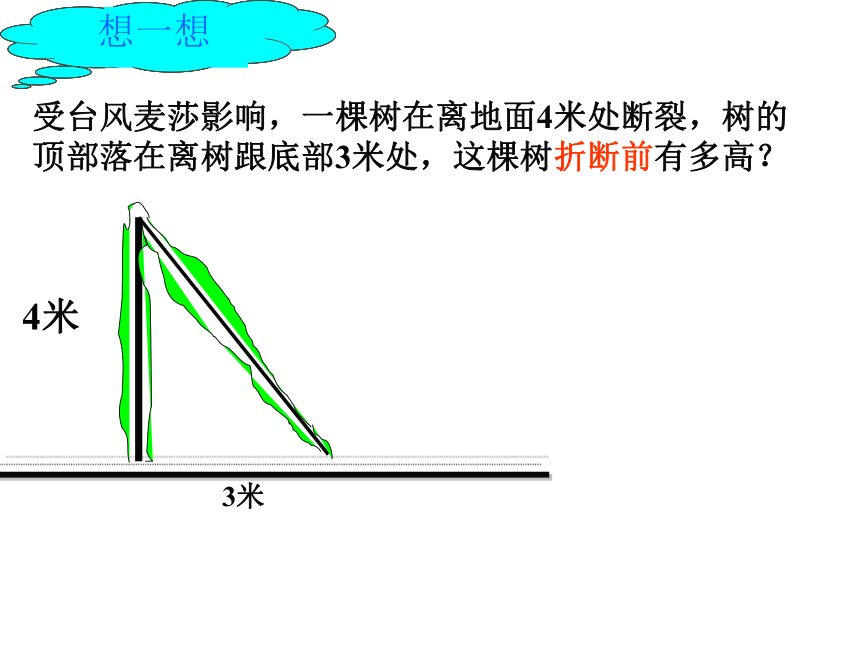
1.两个锐角互余.2.斜边上的中线等于斜边的一半.受台风麦莎影响，一棵树在离地面4米处断裂，树的
顶部落在离树跟底部3米处，这棵树折断前有多高？
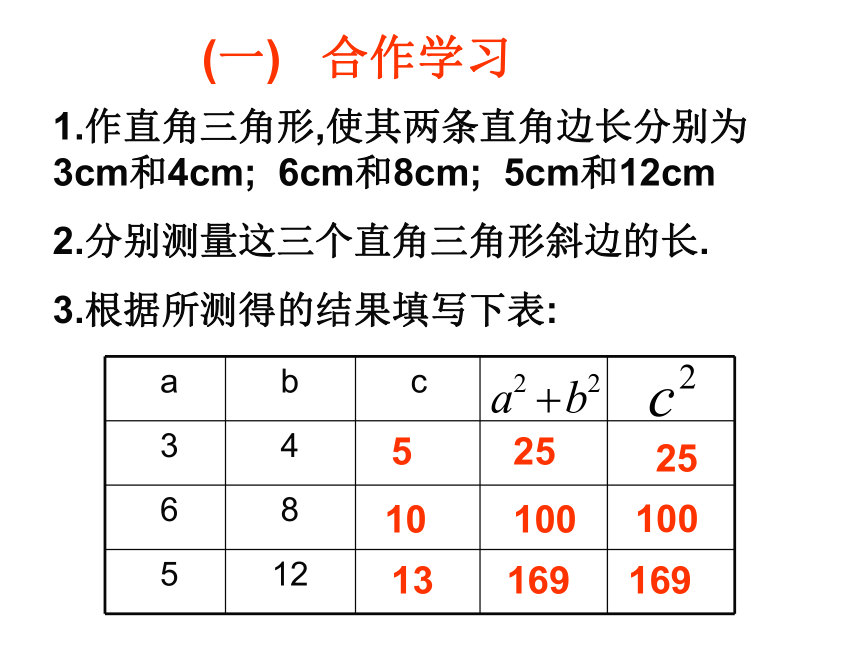
想一想(一) 合作学习1.作直角三角形,使其两条直角边长分别为 3cm和4cm; 6cm和8cm; 5cm和12cm
2.分别测量这三个直角三角形斜边的长.
3.根据所测得的结果填写下表:
525251010010013169169直角三角形的三条边长关系的性质:
直角三角形两条直角边的平方和等于斜边的平方.=ABCbac 如图,∠C=Rt∠,a、b是直角边，c是斜边。在中国古代，人们把弯曲成直角的手臂的上半部分称为"勾"，下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”，较长的直角边称为“股”，斜边称为“弦”.ABCbacabc③①② 如图,∠C=Rt∠,a、b是直角边，c是斜边。求证:a2+b2=c2证明:如图,美国第二十任总统伽菲尔德的证法在数学史上被传为佳话 人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明，
就把这一证法称为“总统”证法。 有趣的总统证法例1.已知ΔABC中, ∠C=Rt∠ ,BC=a,
AC=b,AB=c(1) a=1, b=2, 求c;
(2) a=15, c=17, 求b;练习: P40 T1.2、直角三角形中两条直角边之比为3：4，且斜边为10cm，求（1）两直角边的长（2）斜边上的高线长应用知识回归生活1、如图，受台风麦莎影响，一棵树在离地面4米处断裂，树的顶部落在离树跟底部3米处，这棵树折断前有多高？应用知识回归生活例2.一个长方形零件图,根据所给的尺寸(单位mm),求两孔中心A、B之间的距离.C在平静的湖面上，有一支红莲，高出水面1尺红莲被风一吹，花朵刚好与水面平齐，已知红莲移动的水平距离是2尺问这里水深是多少？
应用知识回归生活思考题3、利用作直角三角形，在数轴上表示点ADBC34 已知∠ACB=Rt∠,
CD⊥AB,AC=3,BC=4.
求CD的长.我来试一试 再 见