探索勾股定理1[上学期]

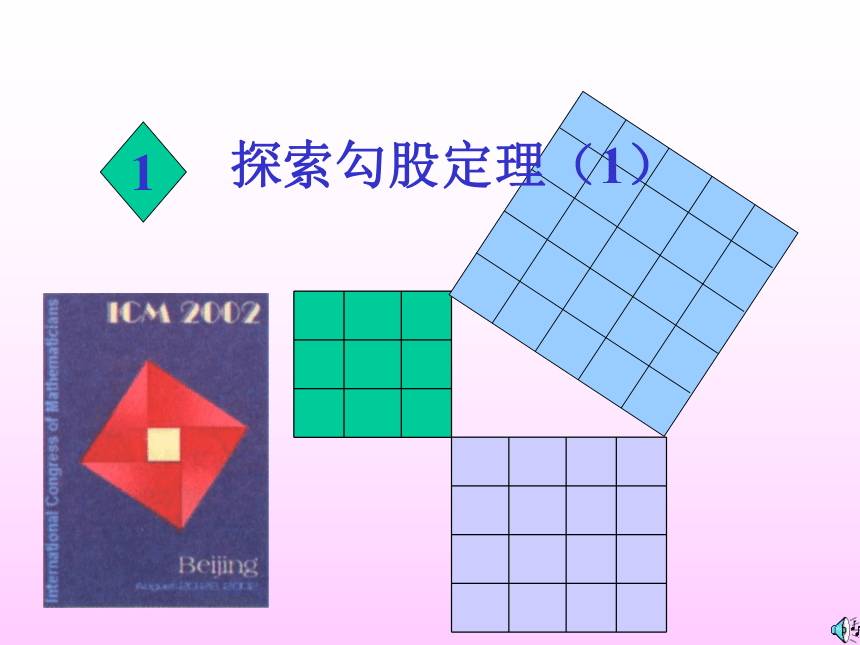
课件21张PPT。 探索勾股定理（1）1 勾股定理——千古第一定理
在古代，许多民族发现了这个事实，即直角三角形的三条边长
为a,b,c，则 ，其中?a,b是直角边长，c是斜边长，我
国的算术《周髀算经》中，就有勾股定理的记载，为了纪念我国古
人的伟大成就，就把这个定理命名为“勾股定理”或“商高定理”，在
西方，被称为“毕达哥拉斯”定理或“百牛”定理。不管怎么说，勾股
定理都是数学中的伟大定理，它给人们的巨大力量可说是难以估量，
乎所有的生产技术和科学研究都离不开它。它的重要性主要表现在：
（1）勾股定理是联系数学最基本的，也是最原始的两个对象
——数与形的第一定理；
（2）勾股定理导致无理数的发现，这就是所谓的第一次数学危机；
（3）勾股定理开始把数学由计算与测量的技术转变为证明和推理
的科学；
（4）勾股定理中的公式是第一个不定方程，有许许多多组数满足
这个方程，也是最早得出完整解答的不定方程，它一方面引导出各
式各样的不定方程，包括著名的费马大定理，另一方面也为不定方
程的解题程序树立了一个范式。
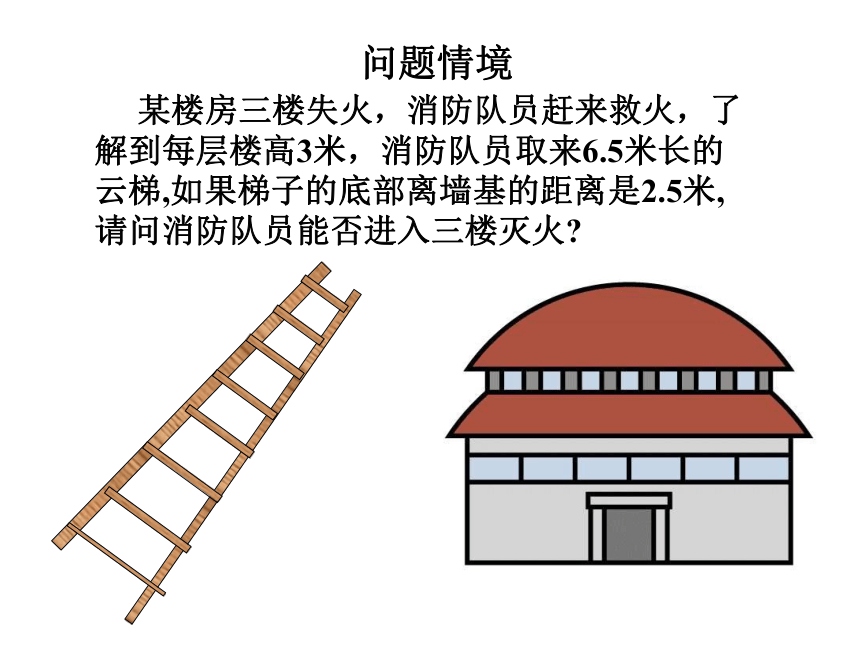
问题情境 某楼房三楼失火，消防队员赶来救火，了解到每层楼高3米，消防队员取来6.5米长的云梯,如果梯子的底部离墙基的距离是2.5米,请问消防队员能否进入三楼灭火? （1）观察图1-1
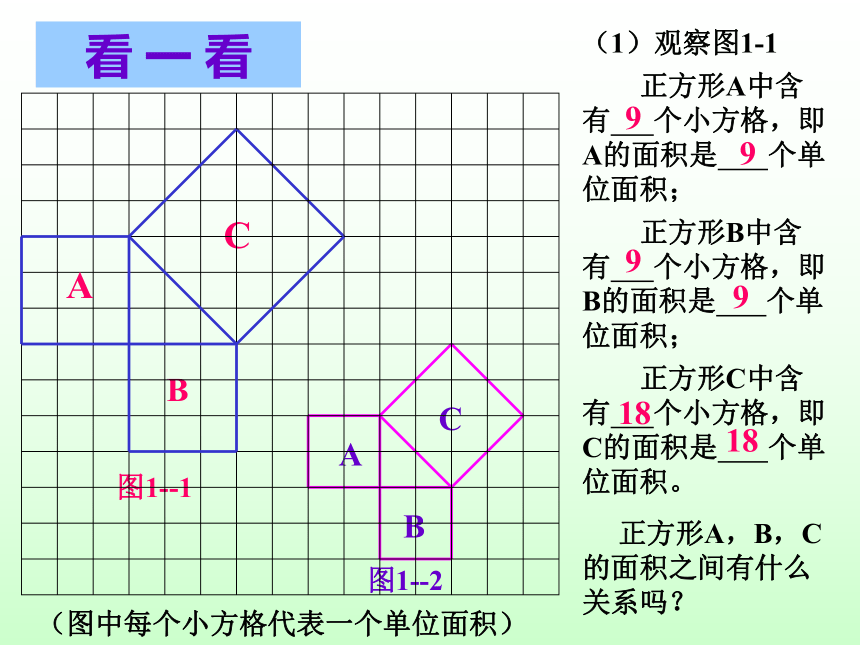
正方形A中含有 个小方格，即A的面积是 个单位面积；
正方形B中含有 个小方格，即B的面积是 个单位面积；
正方形C中含有 个小方格，即C的面积是 个单位面积。
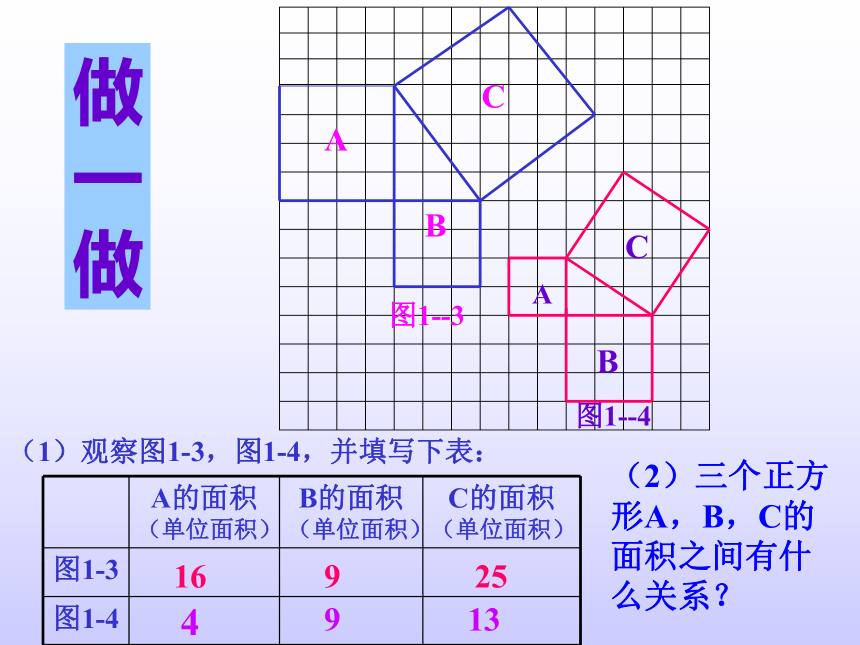
正方形A，B，C的面积之间有什么关系吗？看 一 看 99189918做一做（1）观察图1-3，图1-4，并填写下表：（2）三个正方形A，B，C的面积之间有什么关系？169254913议一议（1）你能用三角形的边长表示正方形的面积吗？
（2）你能发现直角三角形三边长度之间存在什么关系吗？前面得到的规律对这个三角形还成立吗？勾股定理
如果直角三角形两直角边分别为a，b，斜边为c，那么
a2 + b2 = c2即直角三角形两直角边的平方和等于斜边的平方.结论变形直角三角形中，两直角边的平方和等于斜边的平方；
c2=a2 + b2问题解决问题情境 某楼房三楼失火，消防队员赶来救火，了解到每层楼高3米，消防队员取来6.5米长的云梯,如果梯子的底部离墙基的距离是2.5米,请问消防队员能否进入三楼灭火? 赵爽
东汉至三国时代吴国人
为《周髀算经》作注，并著有《勾股圆方图说》幾何原本欧几里得（Euclid of Alexandria; 约 325 B.C. ? 约 265 B.C.）
欧几里的的《几何原本》是用公理方法建立演绎数学体系的最早典范
《几何原本》第一卷的第 47 命題也有对勾股定理的证明。
美国总统的证明加菲（James A. Garfield； 1831 ? 1881）1881 年成为美国第 20 任总统
1876 年提出有关证明想一想 小明妈妈买了一部29英寸（74厘米）的电视机.小明量了电视机的屏幕后，发现屏幕只有58厘米长和46厘米宽，他觉得一定是售货员搞错了.你同意他的想法吗？你能解释这是为什么吗？1这节课你学到了什么知识？
如果直角三角形两直角边分别为a，b，斜边为c，那么 a2 + b2 = c2 即直角三角形两直角边的平方和等于斜边的平方(勾股定理)
2 运用“勾股定理”应注意什么问题？
3、你还有什么疑惑或没有弄懂的地方？小 结：练一练 1. 如图，根据以下数学情境，你可以提出多少个数学问题？你能解决所提出的问题吗？2. 若正方形的面积为2cm2，则它的对角线长是 .
3. 一个直角三角形的三边为三个连续偶数，则它的三边长分别为 .4 .在△ ABC中, ∠C=90°,
(1)若a=5,b=12,则c=__________.
(2)若a=15,c=25,则b=__________.
(3)若c=61,b=60,则a=_________.
(4)若a:b=3:4,c=10,则a=________,b=________.
5 .在直角△ ABC中,a=5,c=13,则△ ABC的面积
S=_____________.
6. 在直角△ ABC中, ∠C=90°,c=20,b=15,则
a=__________.
1. 如图1.1-1,求图中字母M所代表的正方形的面积.


图1.1-1 图1.1-2
2. 如图1.1-2,在四边形ABCD中, ∠ BAD=90°,
∠ CBD=90°,AD=4,AB=3,BC=12,求正方形DCEF
的面积.
?
辨析：△ABC的两边为3和4，求第三边解：由于三角形的两边为3、4
所以它的第三边的c应满足=25 即：c=5 辨析：（1）要用勾股定理解题，首先应具备直角三角
形这个必不可少的条件，可本题△ ABC并未说明它是否
是直角三角形，所以用勾股定理就没有依据。
（2）若告诉△ABC是直角三角形，第三边C也不一定
满足勾股定理，因为题目中并未交待c是斜边
综上所述这个题目条件不足，第三边无法求得。
课后探索 做一个长，宽，高分别为50厘米，40厘米，30厘米的木箱，一根长为70厘米的木棒能否放入，为什么？试用今天学过的知识说明。再见