探索勾股定理(1)[上学期]

课件16张PPT。如图是2002年北京召开的国际数学大会(ICM-2002)的会标.它的设计思路可追溯到3世纪中国数学家赵爽所使用的弦图。用弦图证明勾股定理再数学史上有着重要的地位。2.6 勾股定理（2)合作学习（1）作三个直角三角形，使其两条直角边分别为：
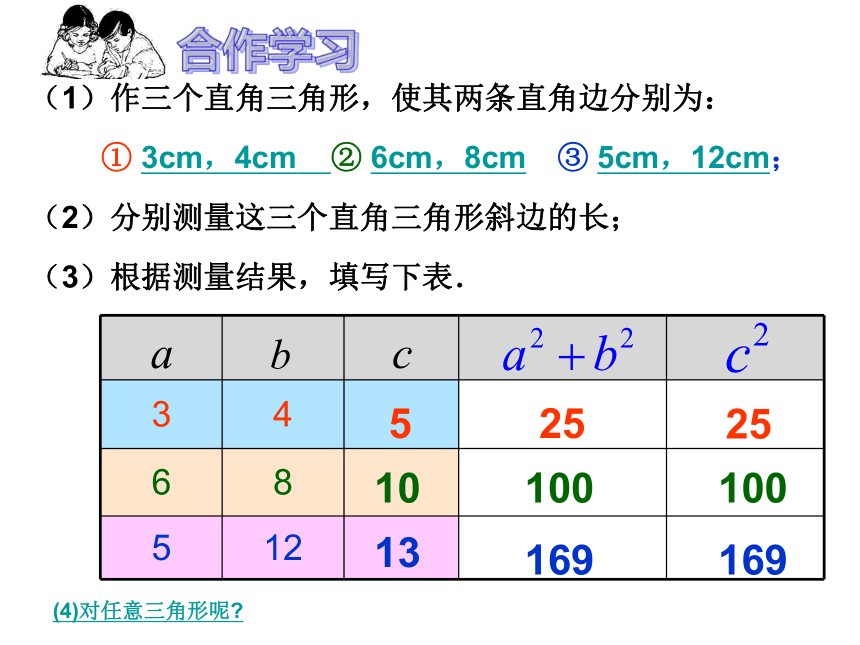
　　 ① 3cm，4cm ② 6cm，8cm　③ 5cm，12cm；
（2）分别测量这三个直角三角形斜边的长；
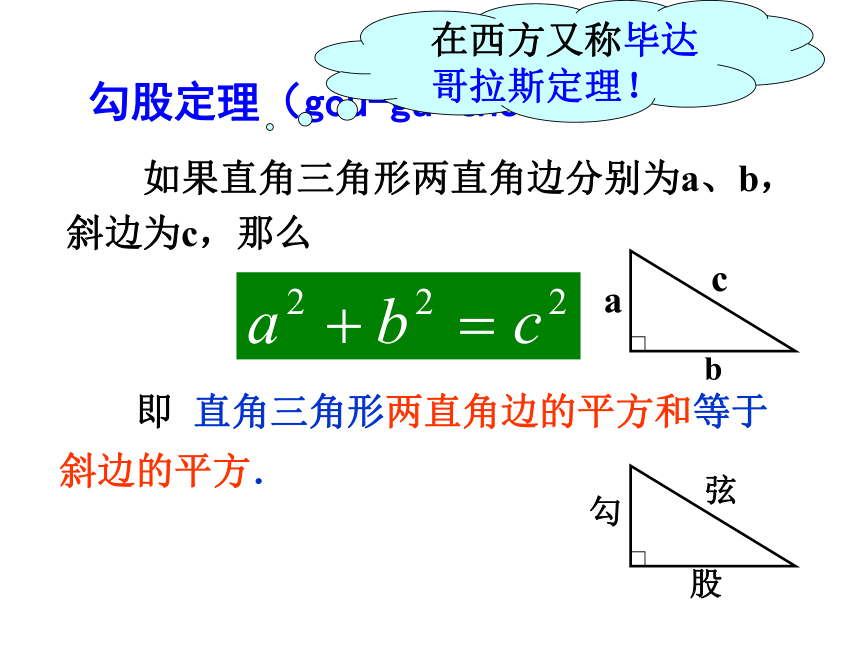
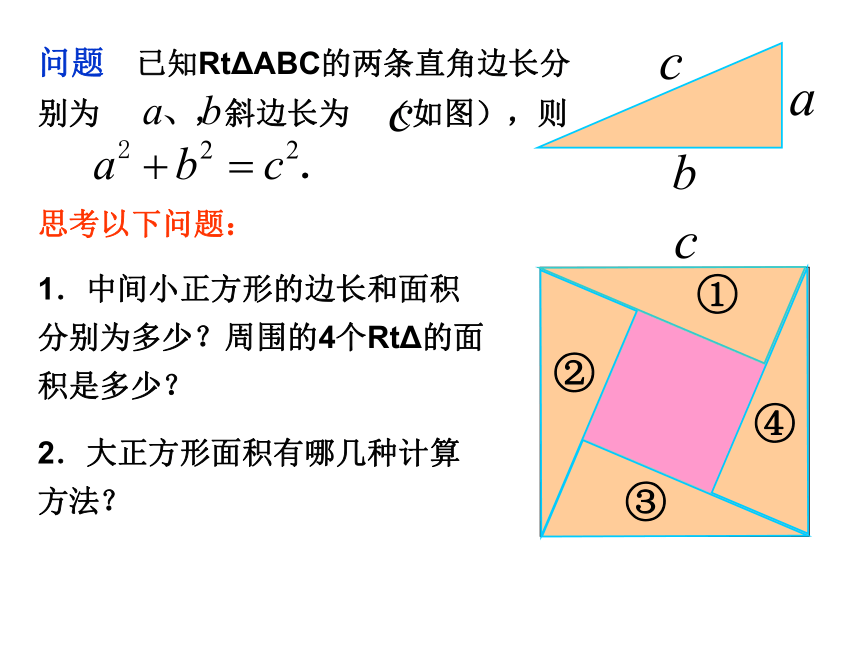
（3）根据测量结果，填写下表．525251010010013169169(4)对任意三角形呢? 勾股定理（gou-gu theorem)　　如果直角三角形两直角边分别为a、b，斜边为c，那么　　即 直角三角形两直角边的平方和等于斜边的平方．勾股弦问题　已知RtΔABC的两条直角边长分别为　　　，斜边长为　（如图），则
①②③④思考以下问题：
1．中间小正方形的边长和面积分别为多少？周围的4个RtΔ的面积是多少？
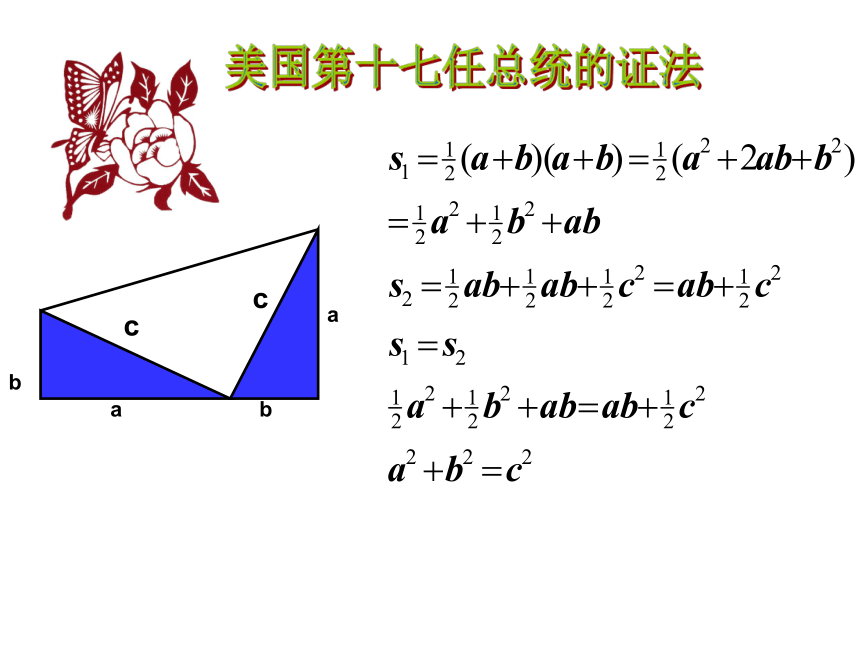
2．大正方形面积有哪几种计算方法？美国第十七任总统的证法例1　已知RtΔABC中，∠C＝Rt∠，BC＝　 ，
　　AC＝　 ，AB＝　 ．
　（1）若　＝1，　＝2，求 ．
　（2）若　＝15， ＝17，求 ．反思：
1．解题时，一定要先弄清哪一条是斜边．
2．你能用刻度尺和圆规，作一条线段，使它的长度
　 为 ？ 练一练：例2　下图是一个长方形零件的平面图，根据所给的尺寸(单位：毫米)，求两孔中心A，B之间的距离．C160904040BA下图中的三角形是直角三角形,其余是正方形,求下列图中字母所表示的正方形的面积.=625=144想一想 一高为2.5米的木梯,架在高为2.4米的墙上(如图),这时梯脚与墙的距离是多少? ABC算一算 小明的妈妈买了一部29英寸（74厘米）的电视机。小明量了电视机的屏幕后，发现屏幕只有58厘米长和46厘米宽，他觉得一定是售货员搞错了。你能解释这是为什么吗？∴售货员没搞错∵议一议荧屏对角线大约为74厘米4658b小 结如果直角三角形两直角边分别为a，b，斜边为c，那么 a2+b2=c2，
即直角三角形两直角边的平方和等于斜边的平方。补充练习：
1、放学以后，小红和小颖从学校分手，分别沿着东南方向和西南方向回家，若小红和小颖行走的速度都是40米/分，小红用15分钟到家，小颖用20分钟到家，小红和小颖家的距离为 （ ）
A、600米； B、800米； C、1000米； D、不能确定
2、直角三角形两直角边分别为5厘米、12厘米，那么斜边上的高是 （ ）
A、6厘米； B、 8厘米； C、 80/13厘米；D、 60/13厘米；
CD3、等腰三角形底边上的高为8，周长为32，求这个三角形的面积8DABC解：设这个三角形为ABC，高为AD，设BD为X，则AB为（16-X）， 由勾股定理得：
X2+82=(16-X)2即X2+64=256-32X+X2∴ X=6∴ S?ABC=BC?AD/2=2 ?6 ?8/2=48再 见