探索勾股定理1[上学期]

课件22张PPT。2.6探索勾股定理(一)一.你们已掌握直角三角形的那些性质?
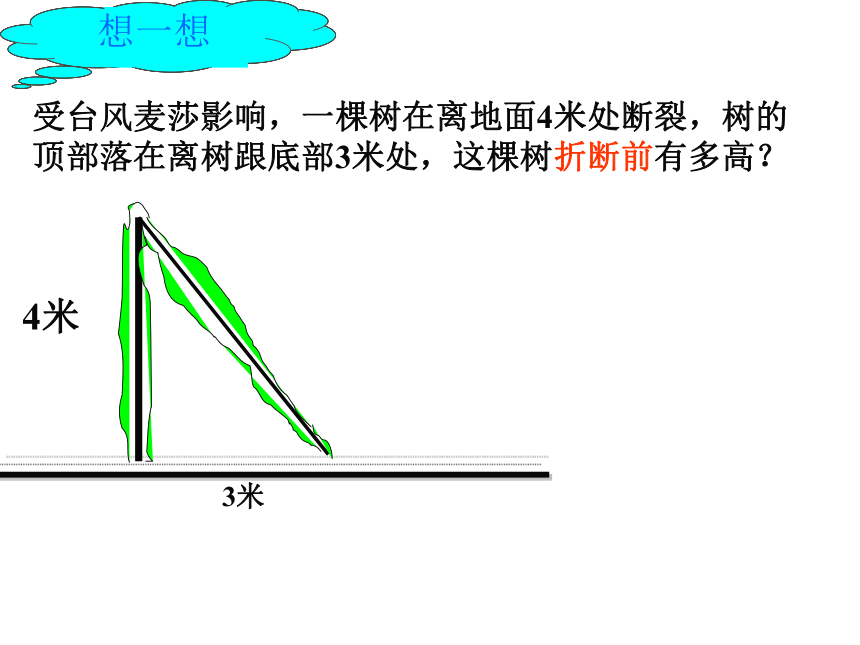
1.两个锐角互余.2.斜边上的中线等于斜边的一半.受台风麦莎影响，一棵树在离地面4米处断裂，树的
顶部落在离树跟底部3米处，这棵树折断前有多高？
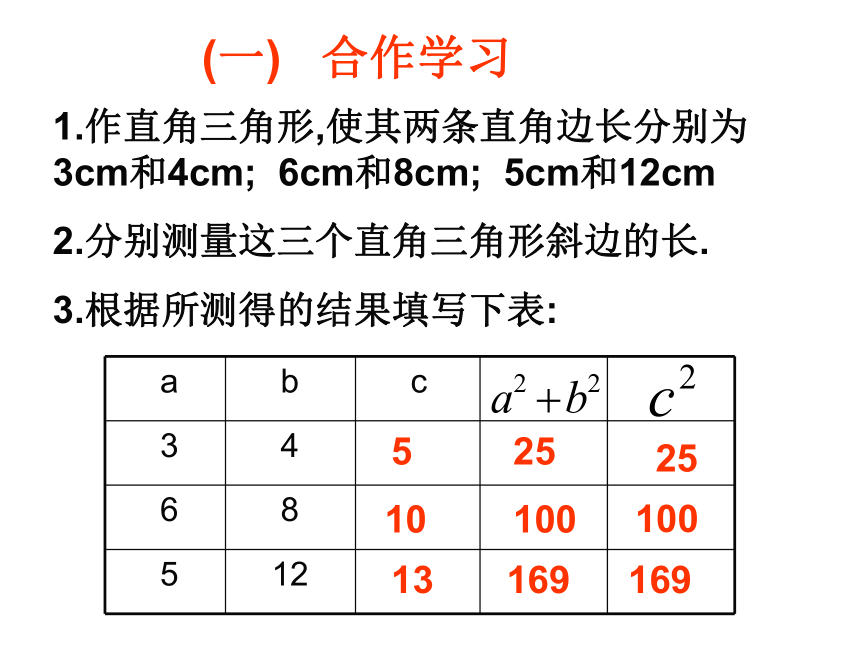
想一想(一) 合作学习1.作直角三角形,使其两条直角边长分别为 3cm和4cm; 6cm和8cm; 5cm和12cm
2.分别测量这三个直角三角形斜边的长.
3.根据所测得的结果填写下表:
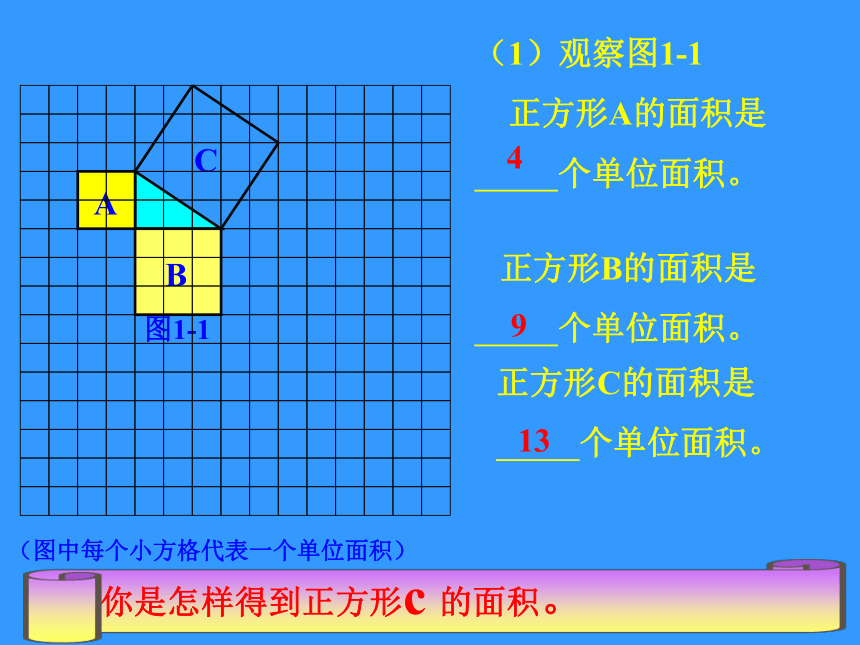
525251010010013169169（1）观察图1-1
正方形A的面积是
个单位面积。 正方形B的面积是
个单位面积。正方形C的面积是
个单位面积。4913你是怎样得到正方形c 的面积。（图中每个小方格代表一个单位面积）直角三角形的三条边长关系的性质:
直角三角形两条直角边的平方和等于斜边的平方.=ABCbac 如图,∠C=Rt∠,a、b是直角边，c是斜边。勾股定理
在中国古代，人们把弯曲成直角的手臂的上半部分称为"勾"，下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”，较长的直角边称为“股”，斜边称为“弦”. 勾股定理——千古第一定理
在古代，许多民族发现了这个事实，即直角三角形的三条边长
为a,b,c，则 ，其中?a,b是直角边长，c是斜边长，我
国的算术《周髀算经》中，就有勾股定理的记载，为了纪念我国古
人的伟大成就，就把这个定理命名为“勾股定理”或“商高定理”，在
西方，被称为“毕达哥拉斯”定理或“百牛”定理。不管怎么说，勾股
定理都是数学中的伟大定理，它给人们的巨大力量可说是难以估量，
乎所有的生产技术和科学研究都离不开它。它的重要性主要表现在：
（1）勾股定理是联系数学最基本的，也是最原始的两个对象
——数与形的第一定理；
（2）勾股定理导致无理数的发现，这就是所谓的第一次数学危机；
（3）勾股定理开始把数学由计算与测量的技术转变为证明和推理
的科学；
（4）勾股定理中的公式是第一个不定方程，有许许多多组数满足
这个方程，也是最早得出完整解答的不定方程，它一方面引导出各
式各样的不定方程，包括著名的费马大定理，另一方面也为不定方
程的解题程序树立了一个范式。
给你四个全等的直角三角形和一个等腰直角三角形，你能否从中选出几个，组成组合图形，并利用组合图形的面积来证明下面的结论:a2+b2=c2
abccc？拼一拼abcabcabcabc==有趣的总统证法
美国第二十任总统伽菲尔德的证法在数学史上被传为佳话
结论变形直角三角形中，两直角边的平方和等于斜边的平方；
c2=a2 + b21、如图，受台风麦莎影响，一棵树在离地面4米处断裂，树的顶部落在离树跟底部3米处，这棵树折断前有多高？应用知识回归生活例1.已知ΔABC中, ∠C=Rt∠ ,BC=a,
AC=b,AB=c(1) a=1, b=2, 求c;
(2) a=15, c=17, 求b;练习: P40 T1.例2.一个长方形零件图,根据所给的尺寸(单位mm),求两孔中心A、B之间的距离.C 小明妈妈买了一部29英寸（74厘米）的电视机，小明量了电视机的屏幕后，发现屏幕只有58厘米长和46厘米宽，他觉得一定是售货员搞错了。你同意他的想法吗？你能解释这是为什么吗？想一想：58厘米46厘米74厘米应用知识回归生活
2、直角三角形中两条直角边之比为3：4，且斜边为10cm，求（1）两直角边的长（2）斜边上的高线长应用知识回归生活3、利用作直角三角形，在数轴上表示点ADBC34 已知∠ACB=Rt∠,
CD⊥AB,AC=3,BC=4.
求CD的长.我来试一试 再 见