2.5直角三角形(1)[上学期]

课件16张PPT。2.5直角三角形(1)直角三角形的两个锐角互余。直角边直角边斜边“直角三角形ABC”用符号“＿＿＿＿＿”表示。Rt△ABC猜想：直角三角形的两个锐角有什么关系？有一个角是直角的三角形叫做直角三角形直角三角形可以用符号“Rt△”解：在△ABC中
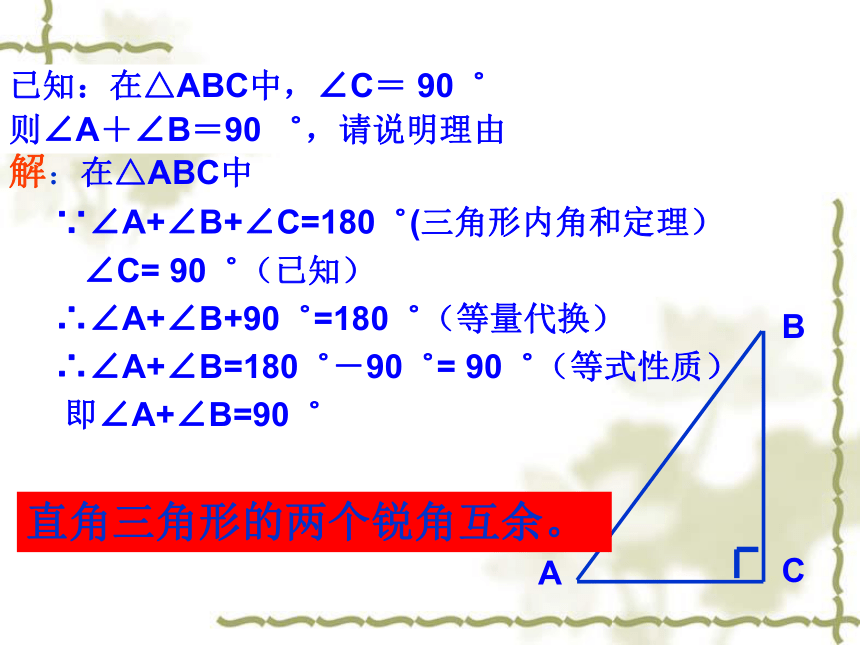
∵∠A+∠B+∠C=180゜(三角形内角和定理）
∠C= 90゜（已知）
∴∠A+∠B+90゜=180゜（等量代换）
∴∠A+∠B=180゜－90゜= 90゜（等式性质）
即∠A+∠B=90゜已知：在△ABC中，∠C＝ 90゜
则∠A＋∠B＝90 ゜，请说明理由直角三角形的两个锐角互余。反过来：有两个角互余的三角形是直角三角形．成立吗？已知：在△ABC中，∠A＋∠B＝90 ゜
求证： △ABC是直角三角形．
　
　（同学们自已完成证明．）直角三角形的两个锐角互余. 反过来，
有两个角互余的三角形是直角三角形.
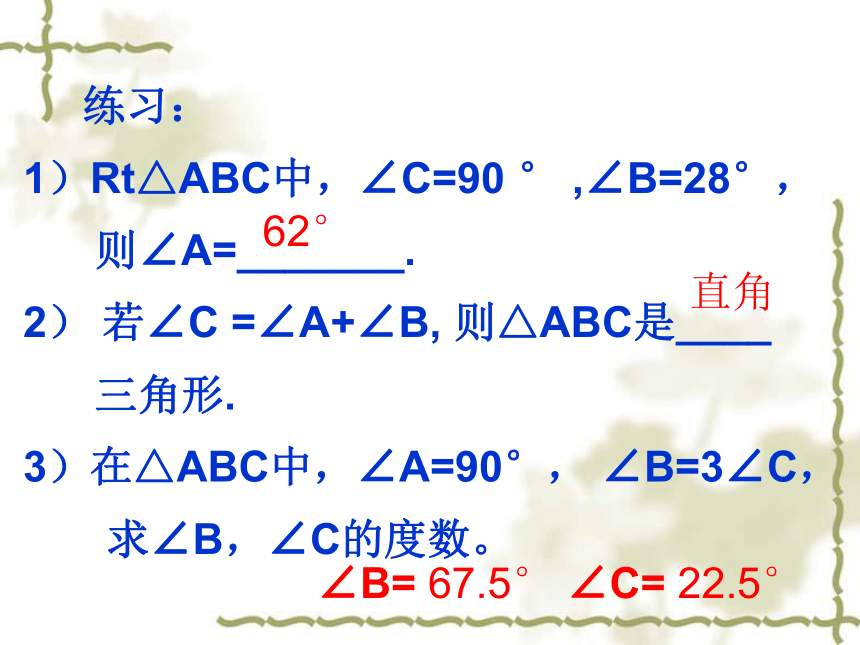
练习：
1）Rt△ABC中，∠C=90 ° ,∠B=28°，
则∠A=_______.
2） 若∠C =∠A+∠B, 则△ABC是____
三角形.
3）在△ABC中，∠A=90°， ∠B=3∠C，
求∠B，∠C的度数。62°直角∠B= 67.5° ∠C= 22.5°　　
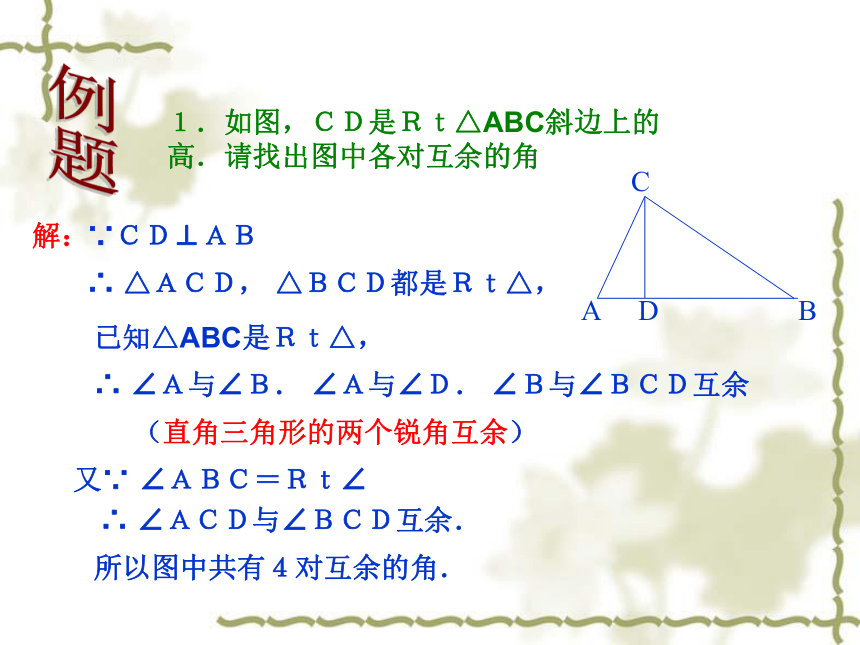
例题１．如图，ＣＤ是Ｒｔ△ABC斜边上的高．请找出图中各对互余的角解：∵ＣＤ⊥ＡＢ∴ △ＡＣＤ， △ＢＣＤ都是Ｒｔ△，已知△ABC是Ｒｔ△，∴ ∠Ａ与∠Ｂ． ∠Ａ与∠Ｄ． ∠Ｂ与∠ＢＣＤ互余（直角三角形的两个锐角互余）又∵ ∠ＡＢＣ＝Ｒｔ∠∴ ∠ＡＣＤ与∠ＢＣＤ互余．所以图中共有４对互余的角．上图中的三角板所表示的三角形有什么特征？
（从边、角方面去说明）等腰直角三角形两条直角边相等的直角三角形叫做等腰直角三角形。ACB它有什么性质呢？1）具有等腰三角形的所有性质
2）具有直角三角形的所有性质∠C=90°，∠A=∠B=45° 例2 如图，在等腰直角三角形ABC中，AD是斜边BC上的高，则AD=BD=CD。请说明理由。D解：在等腰直角三角形ABC中， ∠B= ∠C= 45°∵AＤ⊥ＢC，∴ ∠CAD+ ∠C= 90°（直角三角形的两个锐角互余）∴ ∠CAD= 90°-∠C= 90°- 45°= 45°= ∠C∴AD=DC（在同一个三角形中，等角对等边）同理，AD=BD。∴AD=BD=CD斜边上的高把等腰直角三角形分成两个全等的等腰直角三角形例3、如图，在△ＡBC中，ＡＢ＝ＡＣ， ∠ＢＡＣ＝ 90°，直角∠ＥＰＦ的顶点Ｐ是ＢＣ的中点，两边ＰＥ、ＰＦ分别交ＡＢ、ＡＣ与点Ｅ、Ｆ，则△ＥＰＦ是等腰直角三角形。说明理由ＡＢＣＰＥＦ∠A=30° ∠B=60°4、用一副三角尺拼出甲、乙两个图形，求：
（1）图甲中， ∠ADB的度数；
（2）图乙中， ∠DCF， ∠CFD， ∠AEF的度数ABCDABCDEF甲乙5、将一张长方形纸片按图示方法折叠，得到的△ABC是等腰直角三角形。请说明理由。ABC6、已知一个三角形的三个内角之比为1:1:2，求这个三角形三个内角的度数并说明这是什么形状的三角形。小结：1、直角三角形的定义及表示2、直角三角形的内角的性质3、直角三角形的判定再见作业：作业本