2.5直角三角形[上学期]

课件15张PPT。探究活动任意画一个直角三角形，作出斜边上的中线，并利用圆规比较中线与斜边的一半的长短，你发现了什么？再画几个直角三角形试一试，你的发现相同吗？与同组同学进行交流。操作实践，总结规律．任意画一个直角三角形，作出斜边上的中线，并利用圆规比较中线与斜边的一半的长短．你发现了什么？
（请所有同学把结果都说出来．）
总结：直角三角形性质：
　直角三角形斜边上的中线
　　　　等于斜边的一半
　　∵ ∠C= 90゜
　　　ＣＤ是ＡＢ边上的中线．
　　∴ＣＤ＝　ＡＢ（直角三角形斜边上的中线等于斜边的一半．）ＢＡＣＤ直角三角形斜边上的中线等于斜边的一半 ?
?
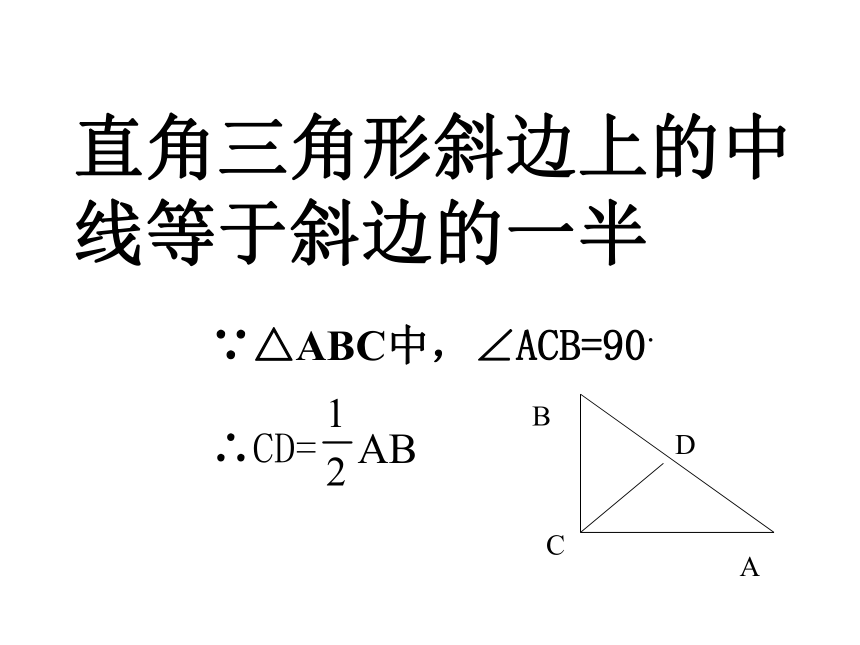
∵△ABC中，∠ACB=90·
∴CD= AB

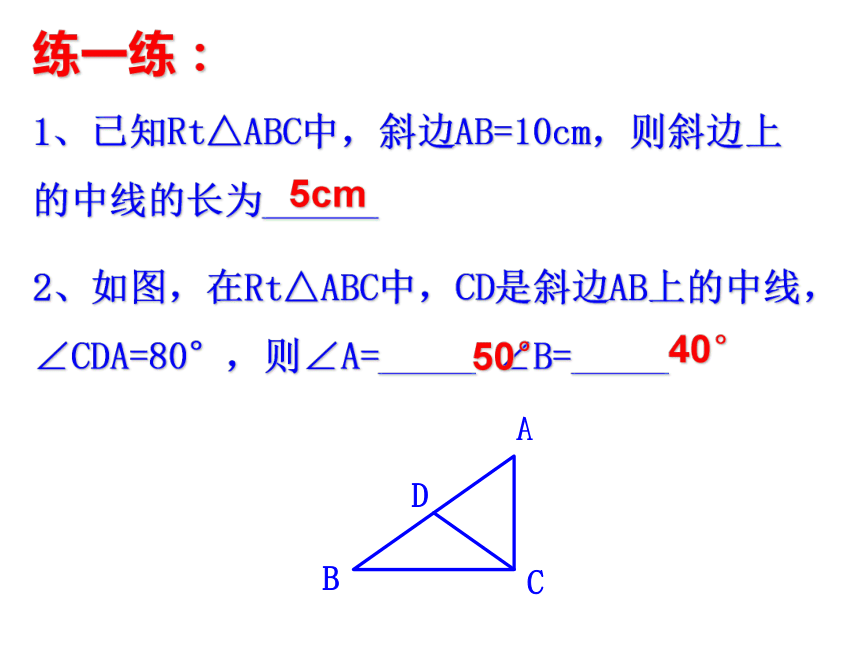
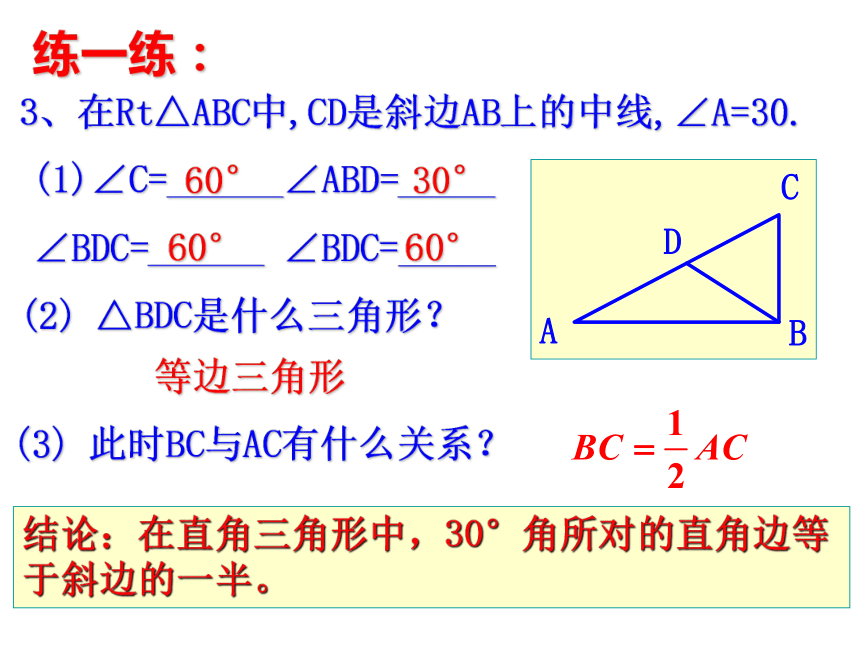
ACDB练一练：1、已知Rt△ABC中，斜边AB=10cm，则斜边上的中线的长为______2、如图，在Rt△ABC中，CD是斜边AB上的中线，∠CDA=80°，则∠A=_____ ∠B=_____5cm50°40°练一练：3、在Rt△ABC中,CD是斜边AB上的中线,∠A=30.(1)∠C=______∠ABD=_____
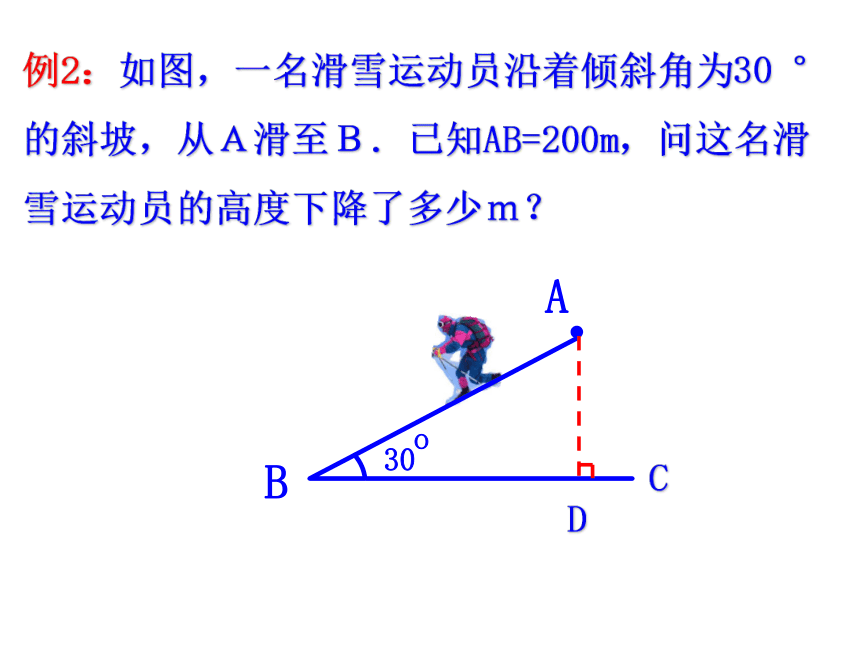
∠BDC=______ ∠BDC=_____(2) △BDC是什么三角形？(3) 此时BC与AC有什么关系？等边三角形结论：在直角三角形中，30°角所对的直角边等于斜边的一半。60°30°60°60°例2：如图，一名滑雪运动员沿着倾斜角为30 °的斜坡，从Ａ滑至Ｂ．已知AB=200m，问这名滑雪运动员的高度下降了多少ｍ？C例1：如图，已知AD⊥BD，AC⊥BC，E为AB的中点，试判断DE与CE是否相等，并说明理由。说明两条线段相等，有时还可以通过第三条线段进行等量代换。３．如图： ∠ＡＢＣ＝ ∠ＡＤＣ
＝９０ ° ，Ｅ是ＡＣ的中点，ＥＦ⊥ＢＤ于Ｆ．试说明Ｆ是ＤＢ的中点．例题ＡＤＣＢＦＥ变式题：如图，已知AD、BE分别是△ABC的BC、AC边上的高，F是DE的中点，G是AB的中点，则FG⊥DE，请说明理由。２．如图：它是人字屋架设计图，其中
ＡＢ＝ＡＣ＝５米．Ｄ是ＡＢ的中点，
ＡＥ⊥ＢＣ．如果∠ＢＡＣ＝１２0゜,
求ＡＥ和ＤＥ的长度．例题ＡＤＢＥＣ如图，在△ABC,∠ACB=90°,CD⊥AB于,
∠A=30 °,则AD等于（ ）能力挑战：（A）4BD （B）3BD
（C）2BD （D）BDB直角三角形的性质小结　１．直角三角形的两个锐角互余．
　２．有两个角互余的三角形是直角三角形．
　３．等腰直角三角形的两个锐角都是４５ ゜４．直角三角形斜边上的中线等于斜边的一半．结论：2、在直角三角形中，30°角
所对的直角边等于斜边的一半。1、直角三角形斜边上
的中线等于斜边的一半。知识复习：∠A+∠B=90°∠A=∠B=45°