２.５直角三角形（一）[上学期]

课件11张PPT。2.5直角三角形[创设情景，引入新课]填空1.三角形内角和为 度2. 有 边相等的三角形叫做等腰三角形；在一个三角形
中，等边对；；3. 在△ABC中，若∠C=900　，则∠A+∠B=[合作交流，探究新知]定义 有一个角是直角的三角形叫做 三角形。表示方法直角三角形用符号 Rt△ 表示，如图所示的三角形
可记做Rt△ABC，其中边AB叫做斜边，BC，AC叫做
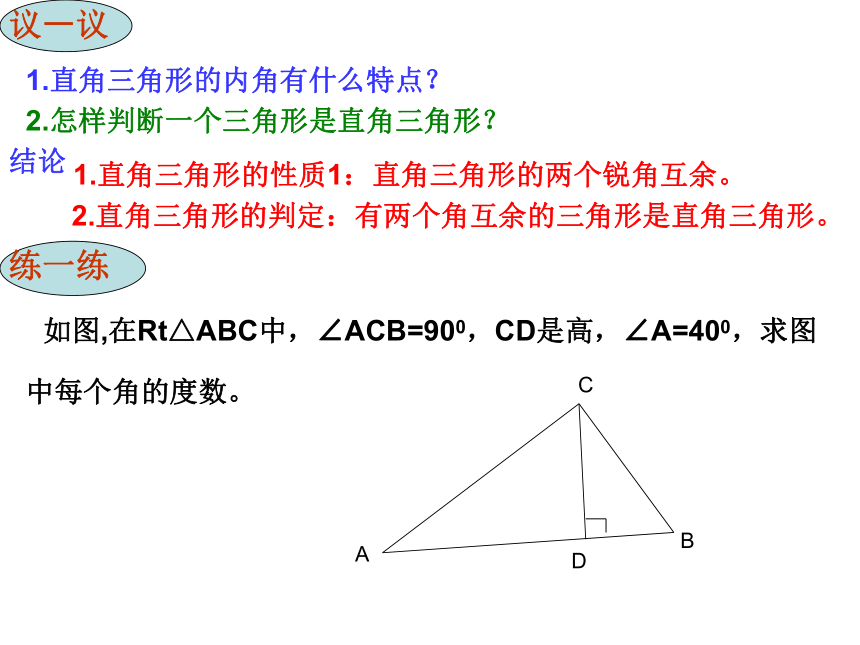
直角边 。┎BCA举例 你能举出直角三角形的应用吗？议一议1.直角三角形的内角有什么特点？2.怎样判断一个三角形是直角三角形？结论1.直角三角形的性质1：直角三角形的两个锐角互余。2.直角三角形的判定：有两个角互余的三角形是直角三角形。练一练如图,在Rt△ABC中，∠ACB=900，CD是高，∠A=400，求图中每个角的度数。ABCD 练习：
1）Rt△ABC中，∠C=90 °，∠B=30°，
则∠A=_______。
2） 若∠C =∠A+∠B， 则△ABC是____
三角形。
3）在△ABC中，∠A=90°，∠B=2∠C，
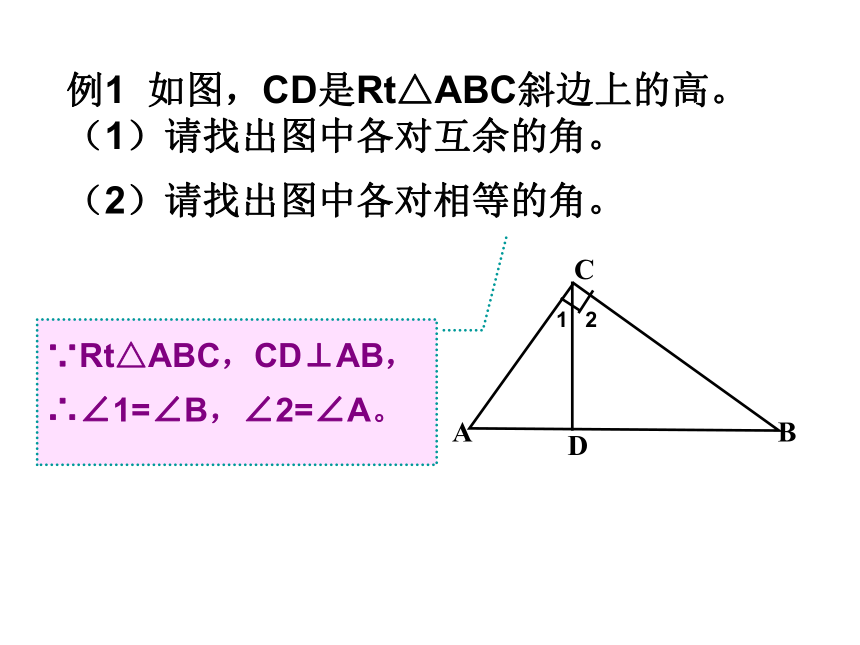
求∠B，∠C的度数。例1 如图，CD是Rt△ABC斜边上的高。
（1）请找出图中各对互余的角。12（2）请找出图中各对相等的角。∵Rt△ABC，CD⊥AB，
∴∠1=∠B，∠2=∠A。上图中的三角板所表示的三角形有什么特征？
（从边、角方面去说明）等腰直角三角形两条直角边相等的直角三角形叫做等腰直角三角形。ACB它有什么性质呢？1）具有等腰三角形的所有性质
2）具有直角三角形的所有性质∠C=90°，∠A=∠B=45°例2 如图，在等腰直角三角形ABC中，AD是斜边BC上的高，则AD=BD=CD。请说明理由。D？练一练在△ABC中，AD⊥BC,∠1=∠B,试说明△ABC为直角三角形
。ＢＣＡＤ１解：∵ AD⊥BC∴∠１＋∠Ｃ＝900∵ ∠1=∠B∴∠B ＋∠Ｃ＝900
∴∠BAC=1800-(∠B ＋∠Ｃ)=900∴△ABC为直角三角形。
［课堂小结］１.直角三角形的概念及其应用的广泛性．２.直角三角形的两个锐角互余．３.有两个角互余的三角形是直角三角形．４.等腰直角三角形的概念及其相关性质．５.注重知识间的相互联系，学会通过比较理解掌握
　相应的几何知识．祝同学们
学习进步！