2.2等腰三角形的性质[上学期]

课件14张PPT。2.2 等腰三角形的性质什么是等腰三角形？
什么是等边三角形？
什么是轴对称图形？有三边相等的三角形叫做等
边三角形。等边三角形也叫
做正三角形。等腰三角形中，相等的两边
叫做腰，另外一边叫做底边，
两腰的夹角叫做顶角，腰和
底边的夹角叫做底角。沿一条直线折过来，直线两
旁的部分能够相互重合的图
形叫做轴对称图形。
这条直线叫做对称轴。
等腰三角形和等边三角形都
是轴对称图形。有两边相等的三角形叫做等
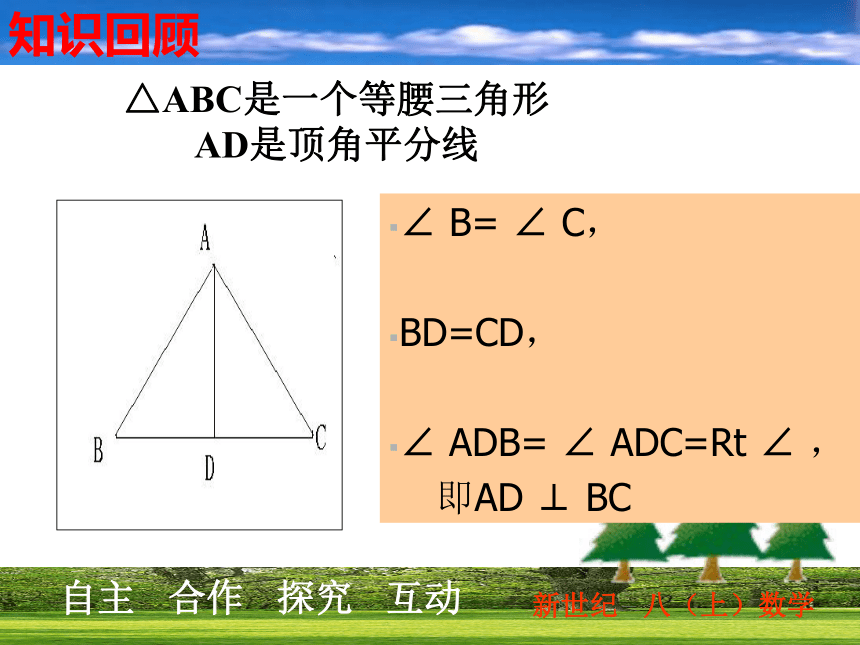
腰三角形。知识回顾知识回顾△ABC是一个等腰三角形AD是顶角平分线∠ B= ∠ C，
BD=CD，
∠ ADB= ∠ ADC=Rt ∠ ，
即AD ⊥ BC等腰三角形性质定理1：
等腰三角形的两个底角相等。
（在一个三角形中，等边对等角）
等腰三角形性质定理2：
等腰三角形的顶角平分线、底边上的中线和高线互相重合。等边三角形的各角相等，并且每一个角都等于60度。 1填空：（根据等腰三角形性质定理及推论）
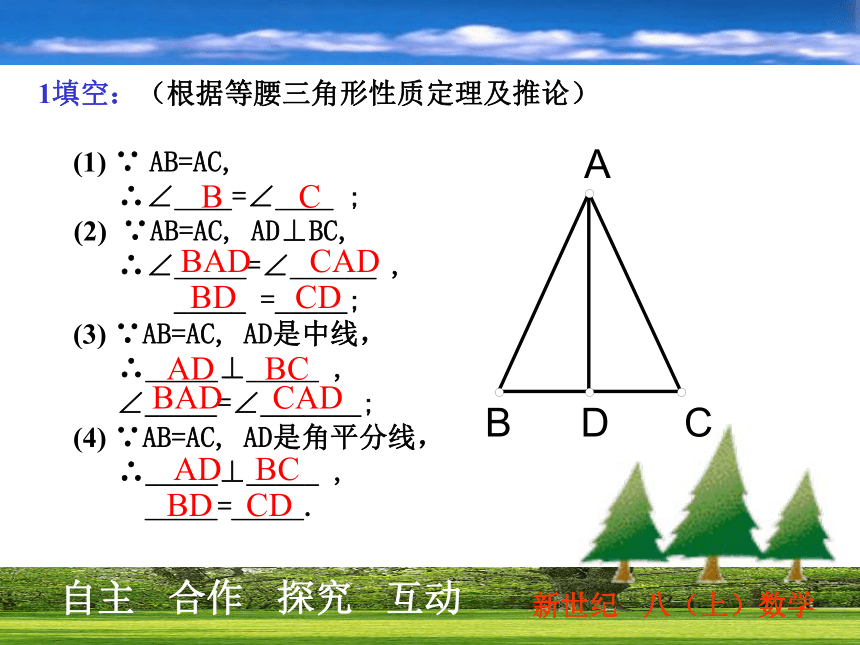
(1) ∵ AB=AC,
∴∠____=∠____ ;
(2) ∵AB=AC, AD⊥BC,
∴∠_____=∠______ ,
_____ =_____;
(3) ∵AB=AC, AD是中线，
∴_____⊥_____ ,
∠_____=∠_______;
(4) ∵AB=AC, AD是角平分线，
∴_____⊥_____ ,
_____=_____.
B CBAD CAD BD CDAD BC BAD CAD
AD BC
BD CD
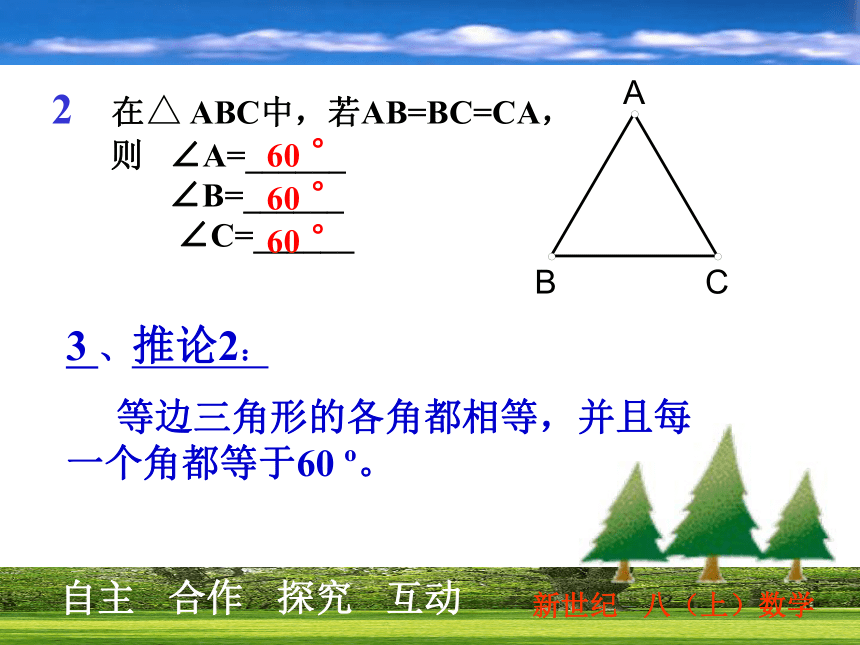
2 在△ ABC中，若AB=BC=CA，
则 ∠A=______
∠B=______
∠C=______
3 、推论2：
等边三角形的各角都相等，并且每一个角都等于60 o。60 °60 °60 °3 口答：
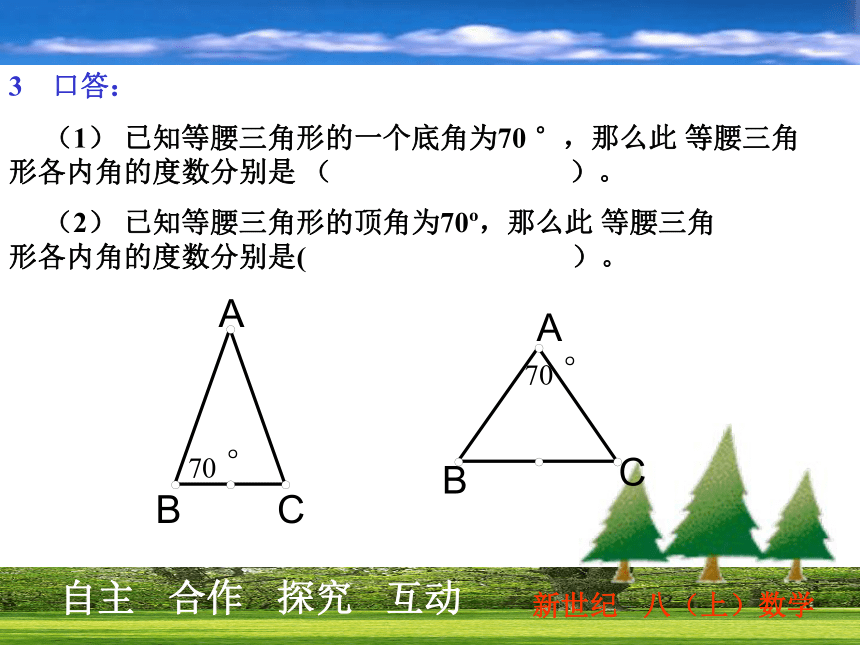
（1） 已知等腰三角形的一个底角为70 °，那么此 等腰三角形各内角的度数分别是 （ ）。 （2） 已知等腰三角形的顶角为70o，那么此 等腰三角形各内角的度数分别是( ）。70 °70 ° （3） 已知等腰三角形的一个内角为70°，那么此 等腰三角形各内角的度数分别是（ ）。
（4） 已知等腰三角形的一个内角为120 °，那么此 等腰三角形各内角的度数分别是（ ）。
例1 如图，在△ABC中，AB=AC,∠A=50o,
求∠B,∠C的度数新世纪八（上）数学自主合作探究互动已知：如图，△ABC中，AB=AC，BD，
CE是∠ABC的角平分线。说明BD=CE成立的理由。证明：∵AB=AC（已知），
∴ ∠ ABC= ∠ ACB
（等腰三角形两底角相等）。
又∵BD平分ABC，CE平分ACB（已知），
∴∠1=1/2 ∠ ABC，∠2=1/2∠ACB
　　（角平分线定义）。
∴∠1=∠2。
又∵∠A=∠A（公共角），
∵AB=AC（已知），
∴△ABD≌△ACE（ASA），
∴BD=CE（全等三角形的对应边相等）。例2：已知如图，△ABC中，AB=AC，O是△ABC内一点，且OB=OC，AO的延长线交BC于D。求证：AD⊥BC，BD=CD。1.在△ABC中，AC=BC：
（1）若∠C=45度，则∠A=_______，∠B=_______；
（2）若∠B=45度，则∠A=_______，∠C=_______；
（3）若∠A=∠C，则∠A=_______，∠B=_______；
2.在△ABC中，已知AB=AC，
AE平分∠CAD，求证：AE∥BC
3 如图所示，D、E为△ ABC一边BC上的两点，已知AD=BD=AE=EC，请问：
（1） 图中有等腰三角形吗？如果有，有几个？是哪几个？
（2） 试证明你的结论。