2.2等腰三角形的性质[上学期]

课件23张PPT。等腰三角形的性质浙江版新教材数学八(上)教材分析〖教学目标〗
◆1、经历利用轴对称变换推导等腰三角形的性质，并加深对轴对称变换的认识.
◆2、掌握等腰三角形的下列性质：等腰三角形的两个底角相等；等腰三角形三线合一．
◆3、会利用等腰三角形的性质进行简单的推理、判断、计算和作图． 教材分析〖教学重点与难点〗
◆教学重点：本节教学的重点是理解并掌握等腰三角形的性质（等边对等角；等腰三角形三线合一）.
◆教学难点：等腰三角形三线合一性质的运用，在解题思路上需要作一些转换，例如例2． 教材分析〖教学方法〗
可采用学生自主探究与教师适当点拨相结合的教学方法．
〖课前准备〗
学生：准备一些等腰三角形纸片
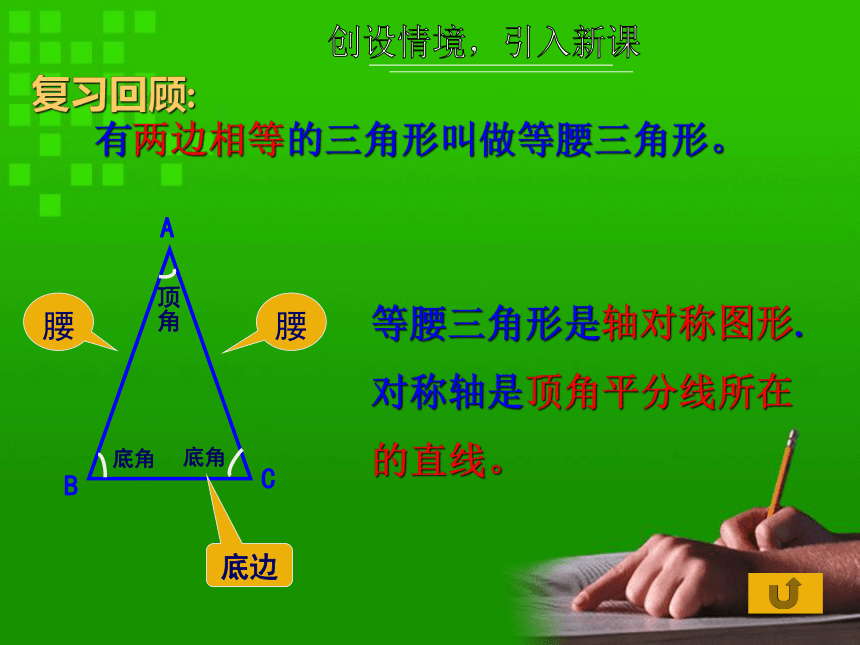
教师：活动任务单，教具，多媒体课件． 教学过程设计有两边相等的三角形叫做等腰三角形。底边复习回顾:等腰三角形是轴对称图形.
对称轴是顶角平分线所在的直线。创设情境，引入新课　　将一把三角尺和一个重锤如图１放置，就能检查一根横梁是否水平，你知道为什么吗？ 请你思考创设情境，引入新课交流互动，探求新知合作学习活动1：如图２，在等腰三角形ABC中，
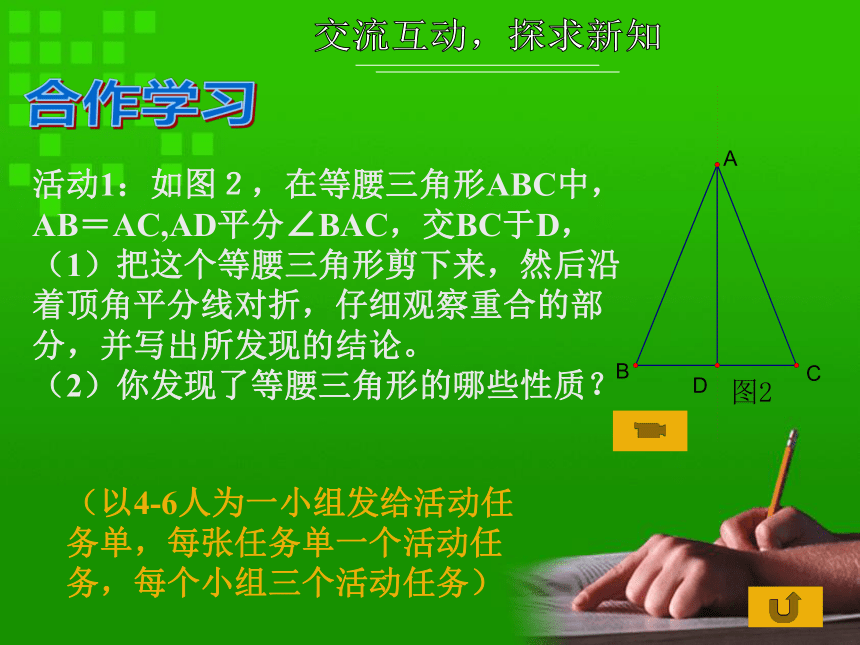
AB＝AC,AD平分∠BAC，交BC于D，
（1）把这个等腰三角形剪下来，然后沿着顶角平分线对折，仔细观察重合的部分，并写出所发现的结论。
（2）你发现了等腰三角形的哪些性质？ （以4-6人为一小组发给活动任务单，每张任务单一个活动任务，每个小组三个活动任务） 合作学习活动2：如图2，在等腰三角形ABC中，AB＝AC,AD平分∠BAC，交BC于D，
（1）等腰三角形ABC的对称轴是什么？△ABD各个顶点的对称点分别是什么？由此可见，将△ABD作关于直线AD的轴对称变换，所得的像是什么？
（2）找出图中的全等三角形，以及所有相等的线段和相等的角。
（3）你有什么发现？能得出等腰三角形的哪些性质？ 合作学习活动3：如图2，在等腰三角形ABC中，AB＝AC,AD平分∠BAC，交BC于D，
（1）根据学过的全等三角形判定方法找出图中的全等三角形，根据全等三角形的性质找出所有相等的线段和角。
（2）你发现了等腰三角形的哪些性质？ 1、等腰三角形的两个底角相等.或 “在同一个三角形中,等边对等角”简称“等腰三角形三线合一”2、等腰三角形的顶角平分线、底边上的中线 和底边上的高互相重合.归纳等腰三角形的性质如下：∵AB=AC，∠1=∠2
∴________________＂等腰三角形三线合一＂的几何语言表述AD⊥BC，BD=CD∵AB=AC，AD⊥BC
∴________________∠1=∠2 ，BD=CD∵AB=AC，BD=CD
∴________________∠1=∠2 ， AD⊥BC例1: 如图,在△ABC中,AB=AC,∠A=80°,
求∠B 和∠C的度数。变式：在△ABC中,　AB=AC，如果将“∠A=80°”改为“∠B=50°”你会求∠A和∠C的度数吗？（1）如图，在△ABC中，AB＝AC，
外角∠DCA＝100°，则∠B＝ 。
80°练习１（2）在△ABC中，AB＝AC，
若∠A＝40°则∠C＝ ；
若∠B＝72°，则∠A＝ 。
（3）在△ABC中，AB＝AC，
∠BAC＝40°，M是BC的中点，
那么∠AMC＝ ，∠BAM＝ 。 70°36°90°20°（1）等腰三角形有一个角是50度，则
另两个角是______________度.65、65或50、80（2）等腰三角形的一个外角等于100度，
则底角是______度.80或50练习2例2: 已知线段a, h,用直尺和圆规作等腰三角形ABC,使底边BC=a, BC边上的高为h.如图，在等腰三角形ABC中，AB=AC，D为BC的中点，则点D到AB，AC的距离相等。请说明理由。练习3合作探究，拓展延伸探究1：
如图，在△ABC中，AB＝AC，直线AE交BC于点D，O是AE上一动点但不与A重合，且OB＝OC，
试猜想AE与BC的关系，并说明你的猜想的理由。 合作探究，拓展延伸探究2：
等腰三角形两底角的平分线大小关系。已知：如图，在△ABC中，AB＝AC，BD、CE分别是两底角的平分线。
试猜想BD与CE的关系，并说明你的猜想的理由。归纳梳理，形成结构在本节课的学习中，你有哪些收获和困惑？ 布置作业，课外延伸必做作业
1．作业本
2．课后作业题1-4
选做作业:
（探究2延伸）试探究等腰三角形两腰上的中线、高线大小关系。 ?
?
板 书 设 计2.２等腰三角形的性质
性质１：　　　　例１ ：
性质２： 　　　　例２ ：
（板演区）