2.2等腰三角形[上学期]

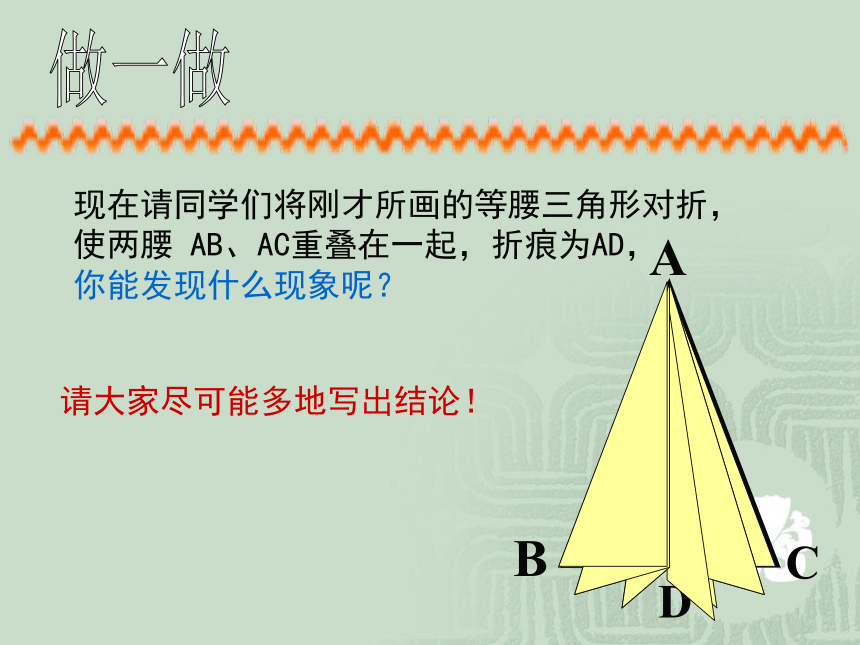
课件15张PPT。等腰三角形的性质做一做现在请同学们将刚才所画的等腰三角形对折，
使两腰 AB、AC重叠在一起，折痕为AD，
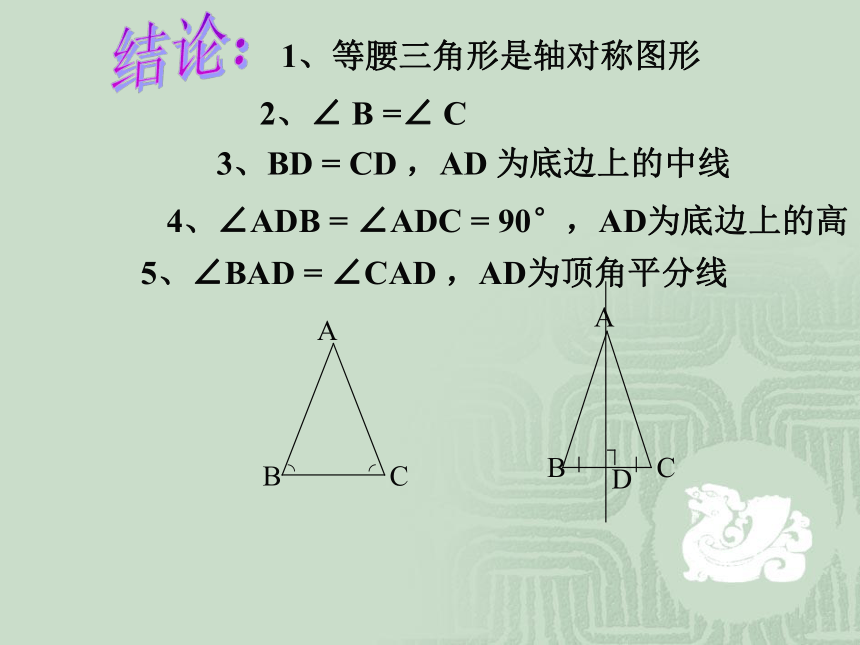
你能发现什么现象呢？请大家尽可能多地写出结论！结论：1、等腰三角形是轴对称图形2、∠ B =∠ C3、BD = CD ，AD 为底边上的中线4、∠ADB = ∠ADC = 90°，AD为底边上的高5、∠BAD = ∠CAD ，AD为顶角平分线等腰三角形的性质:
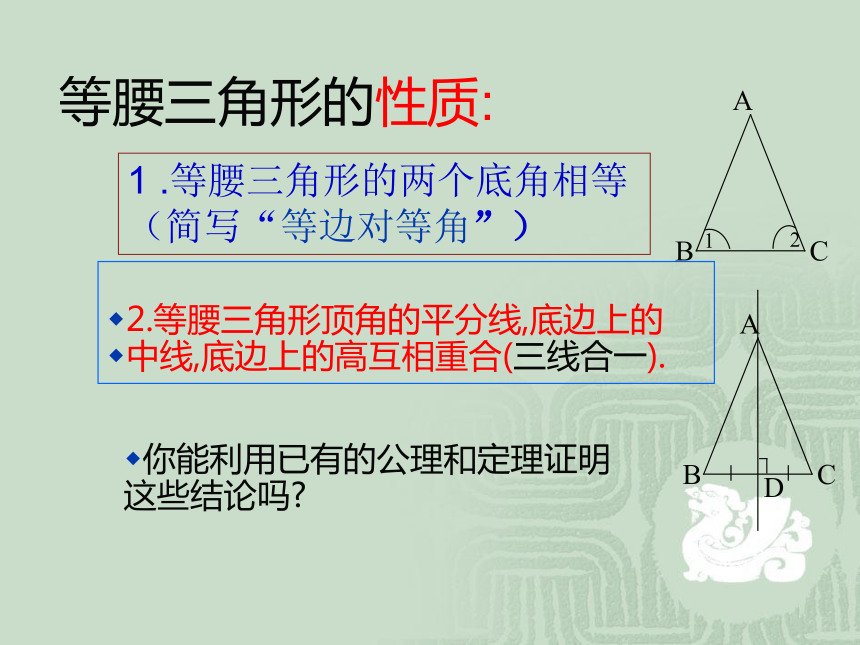
2.等腰三角形顶角的平分线,底边上的
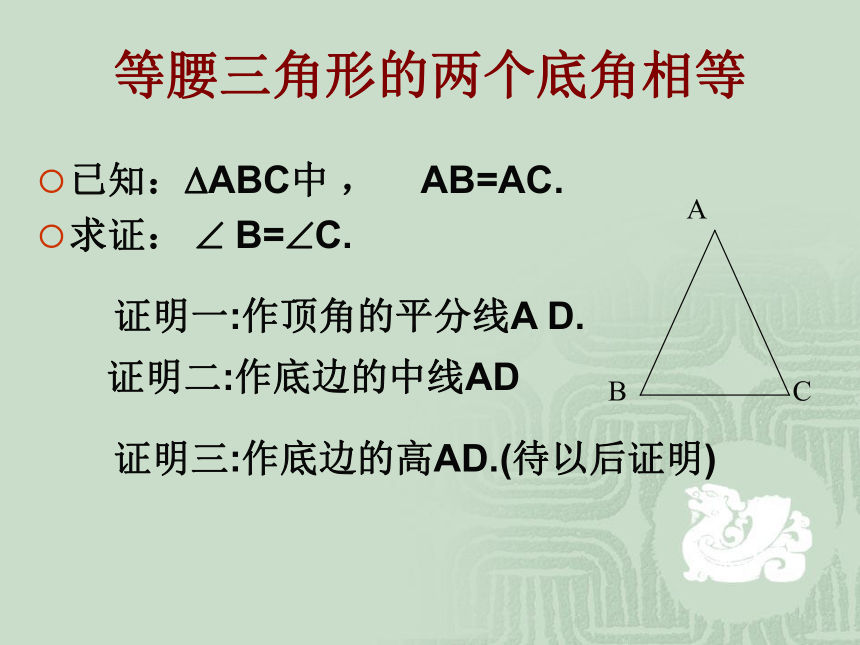
中线,底边上的高互相重合(三线合一).你能利用已有的公理和定理证明这些结论吗?1 .等腰三角形的两个底角相等 （简写“等边对等角”）等腰三角形的两个底角相等已知：?ABC中 ， AB=AC.
求证： ? B=?C.
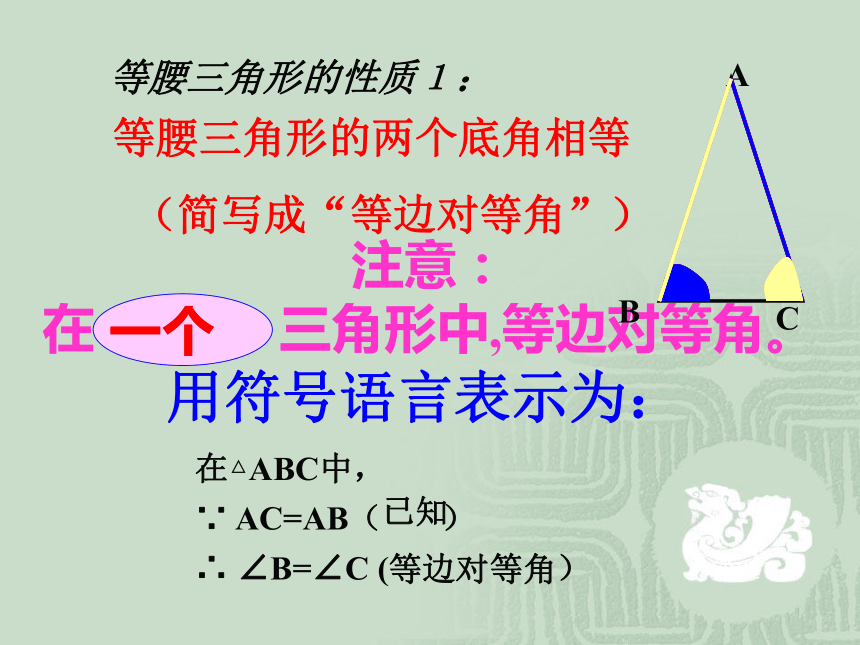
证明一:作顶角的平分线A D.证明二:作底边的中线AD证明三:作底边的高AD.(待以后证明)等腰三角形的性质１： 等腰三角形的两个底角相等
（简写成“等边对等角”）注意：
在 三角形中,等边对等角。用符号语言表示为：在△ABC中，
∵ AC=AB（ ）
∴ ∠B=∠C ( ）已知等边对等角在△ABC中
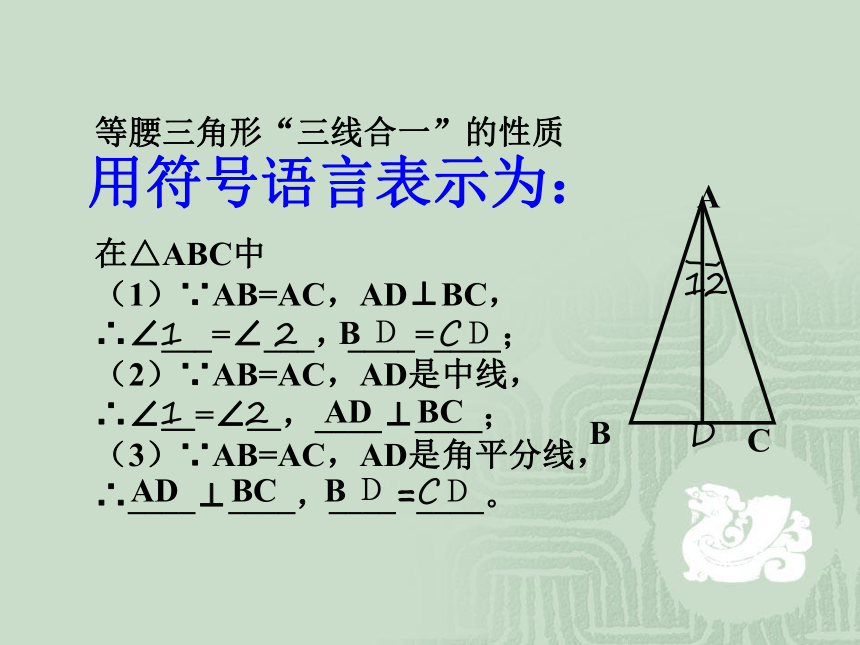
（1）∵AB=AC，AD⊥BC，
∴∠___=∠___，____=____；
（2）∵AB=AC，AD是中线，
∴∠＿=∠＿，____⊥____；
（3）∵AB=AC，AD是角平分线，
∴____⊥____，____=____。 等腰三角形“三线合一”的性质用符号语言表示为：12B ＤCＤ12ADBCADBCB ＤCＤ例1、已知：在△ABC中，AB = AC，
∠A = 50°， 求∠B 和 ∠C的度数。ABC变式练习1:已知：在△ABC中，AB = AC，
∠A = 50°， 求∠B 和 ∠C的度数。BA变式练习2:已知：等腰三角形的一个
内角为 50 °， 求另两个角的度数.例2 已知线段a, h,用直尺和圆规作等腰三角形ABC,使底边BC=a, BC边上的高为h.ha作法:1.作线段BC=a.2.作BC的中垂线m,交BC于点D.3.在直线 m上截取DA=h,连接AB,AC.△ABC就是所求的等腰三角形.练习判断下列语句是否正确。（1）等腰三角形的角平分线、中线和高互相重合。（ ）
（2）有一个角是60°的等腰三角形，其它两个
内角也为60°. （ ）
（3）等腰三角形的底角都是锐角. （ ）
（4）钝角三角形不可能是等腰三角形 . （ ）××作业 75°, 30°70°,40°或55°,55°35°,35°巩固练习1.填空题：
(1)如图,在△ ABC中,AB=AC,外角∠ ACD=100,则∠ B=____度
(2)如图,在等腰三角形ABC中,AB=AC,D为BC的中点,则点D到AB,AC的距离相等.请说明理由.
　 ABCD100 °第１题ＡＢＣＥＦＤ第２题文字叙述几何语言等腰三角形的两底角相等（简称等边对等角）∵AB=AC
∴∠B=∠C等腰三角形顶角的平分线平分底边并且垂直于底边（简称三线合一）∵AB=AC，∠1=∠2 ∴AD⊥BC，BD=CD课堂小结布置作业：课本
第２６页
１，２，３，４．