一元一次方程的应用(5)--工程问题 浙教版[上学期]
文档属性
| 名称 | 一元一次方程的应用(5)--工程问题 浙教版[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 248.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-12-08 22:41:00 | ||
图片预览




文档简介
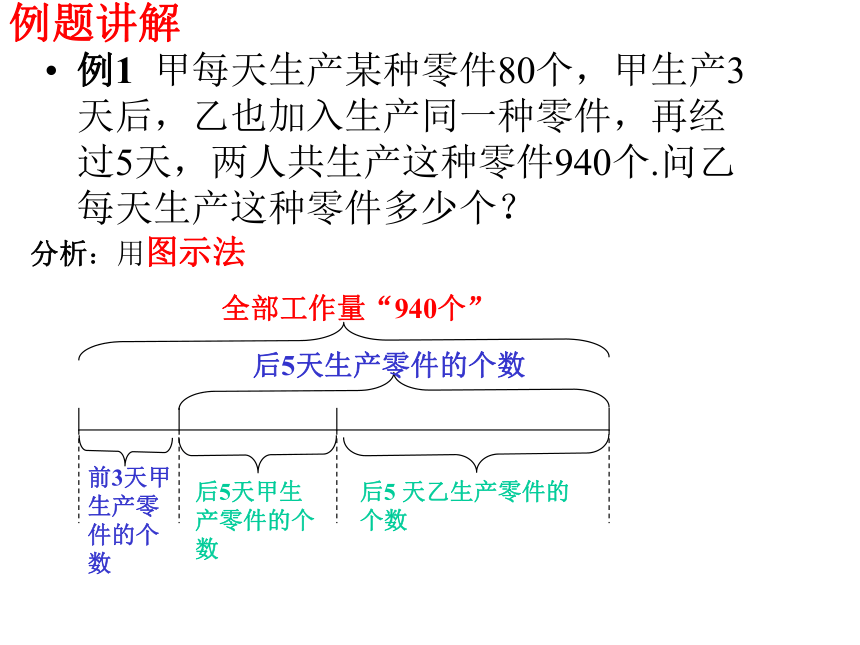
课件18张PPT。一元一次方程的应用(五)工程问题工程问题中的数量关系:1) 工作效率=2)工作总量=工作效率×工作时间3)工作时间=4)各队合作工作效率=各队工作效率之和5)全部工作量之和=各队工作量之和例1 甲每天生产某种零件80个,甲生产3天后,乙也加入生产同一种零件,再经过5天,两人共生产这种零件940个.问乙每天生产这种零件多少个?分析:用图示法
例题讲解练习1: p130 1分析:1、如何设未知数?工作总量如何表示?
2、甲、乙的工作效率如何表示?
3、等量关系怎样?
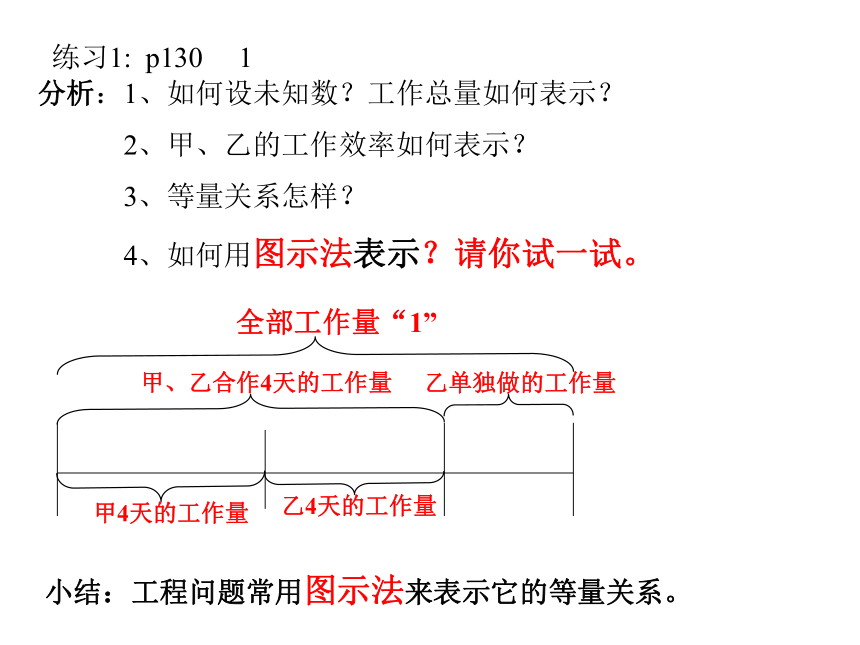
4、如何用图示法表示?请你试一试。
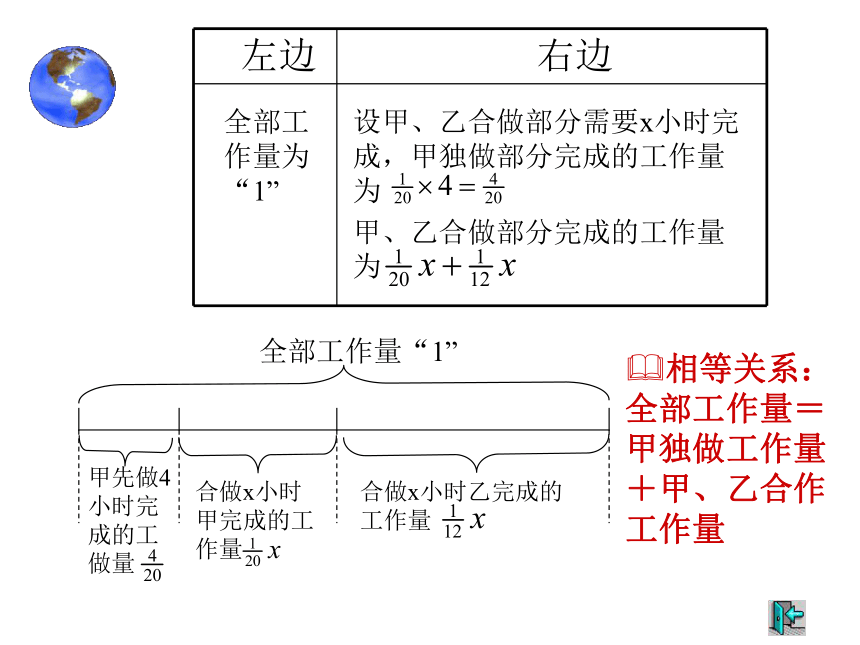
小结:工程问题常用图示法来表示它的等量关系。练习2、一件工作,甲单独做20个小时完成,乙单独做12小时完成,现在先由甲单独做4小时,剩下的部分由甲、乙合做。剩下的部分需要几小时完成?相等关系:全部工作量=甲独做工作量+甲、乙合作工作量
全部工作量为“1”
设甲、乙合做部分需要x小时完成,甲独做部分完成的工作量为
甲、乙合做部分完成的工作量为
解:设剩下的部分需要x小时完成,根据题意,得
解这个方程,得
x=6
答:剩下的部分需要6小时完成。 注意:工作量=工作效率×工作时间练习2、一件工作,甲单独做20个小时完成,乙单独做12小时完成,现在先由甲单独做4小时,剩下的部分由甲、乙合做。剩下的部分需要几小时完成?注意:这整个圆的面积表示全部工作量1,圆型示意图可以使我们对于“把全部工作量看成1”有更直观的认识。合作部
分乙完
成的工
作量x/12甲独做部
分完成的
工作量
4/20
合做部分
甲完成的
工作量x/20
课练二:2、某工作由甲、乙两队单独做分别需要3小时、5小时,求两人合做这项工作的80%需要几小时?解:设两人合做这项工做需x小时,根据题意得,
(1/3+1/5)x=80%
解这个方程得
x=3/2
答:两人合做这项工做的80%需3/2小时。例题讲解例2 挖一条长为1210米长的水渠,由甲施工队独做需要11
天完成,乙施工队独做需要20天完成,现在甲、乙两
施工队从两头同时施工,挖完这条水渠估计需几天?
等量关系:
甲施工队挖的米数+乙施工队挖的米数=1210米答:两个施工队合作估计需要八天挖完。解:设挖完这条水渠估计要x天.依题意得x ≈8 分析:把这个问题看成工程问题的话,
通常把总量(即本题中的这条水渠)看成“1”,由题意得:例题讲解例2 挖一条长为1210米长的水渠,由甲施工队独做需要11
天完成,乙施工队独做需要20天完成,现在甲、乙两
施工队从两头同时施工,挖完这条水渠估计需几天?
即本题的等量关系为例1中的1210这个数据可以不用,解方程也简单。甲完成工作量+乙完成工作量=1x ≈8解:设挖完这条水渠估计要x天.例3 修筑一条公路,甲工程队单独承包要80天完成,乙工程队单独
承包要120天完成
1)现在由两个工程队合作承包,几天可以完成?
2)如果甲、乙两工程队合作了30天后,因甲工作队另有任务,
剩下工作由乙工作队完成,则修好这条公路共需要几天?
解: 1)设两工程队合作需要x天完成。
2)设修好这条公路共需要 y 天完成。
等量关系: 甲30天工作量+乙队y天的工作量 = 1
答:两工程队合作需要48天完成,修好这条公路还需75天。等量关系:甲工作量+乙工作量=1
依题意得
依题意得y=75x=48 依题意得:
x=10
答:两管同时注油10小时可注满油轮的例4等量关系:甲管注油量+乙管注油量=解:设两管同时注油需x小时可注满油轮的
例5 已知开管注水缸,10分钟可满,拨开底塞,满缸水20 分钟流完,缸内的水流完后,现若管、塞同开,若干时间后,将底塞塞住,又过了2倍的时间才注满水缸,求管塞同开的时间是几分钟?分析: 解:设两管同开x分钟
等量关系:注入量-放出量=缸的容量
依题意得: x=4
答:管塞同开的时间为4分钟x+2x=3x(分钟)x(分钟)解:设再经过x小时水槽里的水恰好等于水槽的等量关系:甲管流进水的水+乙管流出的水 =水槽的 依题意得:
,5例、一个水槽有甲、乙两个水管。甲水管是进水管, 在5小时之内可以把空水槽装满。乙水管是出水管,满槽的水在6小时内可以流完。现水槽内没有水,如果先开甲水管1小时,再把乙水管也打开,再经过几小时5水槽里的水恰好等于水槽容量的? 18答:再经过 小时水槽里的水恰好是水槽容量的例7 一个水池装甲、乙、丙三根水管,单开甲管10小时
可注满水池,单开乙管15小时可注满,单开丙管20
小时可注满。现在三管齐开,中途甲管关闭,结果6
小时把水池注满,问甲管实际开了几个小时?
解:设甲管实际开了x小时
等量关系:甲管x小时的工作量+乙、丙两管同开
6 小时的工作量)= 1
答:甲管实际开了3小时。
依题意得:
x=3等量关系:4天的工作量+改进后(x – 4)工作量= 0.5解:设一共x天可以修完它的一半。
依题意得 ×4+ (x—4)= 0.5
答:一共 天可以修完它的一半。例7分析:x=小结:
1)工程问题或称工作量问题,一定要掌握效率、时间、总量三者之间的关系。 2)部分工作量+部分工作量=总量
解题关键是:审清题意,能用表格法、线段示意图法对题目进行分析。找准相等关系,从而列出方程。
例题讲解练习1: p130 1分析:1、如何设未知数?工作总量如何表示?
2、甲、乙的工作效率如何表示?
3、等量关系怎样?
4、如何用图示法表示?请你试一试。
小结:工程问题常用图示法来表示它的等量关系。练习2、一件工作,甲单独做20个小时完成,乙单独做12小时完成,现在先由甲单独做4小时,剩下的部分由甲、乙合做。剩下的部分需要几小时完成?相等关系:全部工作量=甲独做工作量+甲、乙合作工作量
全部工作量为“1”
设甲、乙合做部分需要x小时完成,甲独做部分完成的工作量为
甲、乙合做部分完成的工作量为
解:设剩下的部分需要x小时完成,根据题意,得
解这个方程,得
x=6
答:剩下的部分需要6小时完成。 注意:工作量=工作效率×工作时间练习2、一件工作,甲单独做20个小时完成,乙单独做12小时完成,现在先由甲单独做4小时,剩下的部分由甲、乙合做。剩下的部分需要几小时完成?注意:这整个圆的面积表示全部工作量1,圆型示意图可以使我们对于“把全部工作量看成1”有更直观的认识。合作部
分乙完
成的工
作量x/12甲独做部
分完成的
工作量
4/20
合做部分
甲完成的
工作量x/20
课练二:2、某工作由甲、乙两队单独做分别需要3小时、5小时,求两人合做这项工作的80%需要几小时?解:设两人合做这项工做需x小时,根据题意得,
(1/3+1/5)x=80%
解这个方程得
x=3/2
答:两人合做这项工做的80%需3/2小时。例题讲解例2 挖一条长为1210米长的水渠,由甲施工队独做需要11
天完成,乙施工队独做需要20天完成,现在甲、乙两
施工队从两头同时施工,挖完这条水渠估计需几天?
等量关系:
甲施工队挖的米数+乙施工队挖的米数=1210米答:两个施工队合作估计需要八天挖完。解:设挖完这条水渠估计要x天.依题意得x ≈8 分析:把这个问题看成工程问题的话,
通常把总量(即本题中的这条水渠)看成“1”,由题意得:例题讲解例2 挖一条长为1210米长的水渠,由甲施工队独做需要11
天完成,乙施工队独做需要20天完成,现在甲、乙两
施工队从两头同时施工,挖完这条水渠估计需几天?
即本题的等量关系为例1中的1210这个数据可以不用,解方程也简单。甲完成工作量+乙完成工作量=1x ≈8解:设挖完这条水渠估计要x天.例3 修筑一条公路,甲工程队单独承包要80天完成,乙工程队单独
承包要120天完成
1)现在由两个工程队合作承包,几天可以完成?
2)如果甲、乙两工程队合作了30天后,因甲工作队另有任务,
剩下工作由乙工作队完成,则修好这条公路共需要几天?
解: 1)设两工程队合作需要x天完成。
2)设修好这条公路共需要 y 天完成。
等量关系: 甲30天工作量+乙队y天的工作量 = 1
答:两工程队合作需要48天完成,修好这条公路还需75天。等量关系:甲工作量+乙工作量=1
依题意得
依题意得y=75x=48 依题意得:
x=10
答:两管同时注油10小时可注满油轮的例4等量关系:甲管注油量+乙管注油量=解:设两管同时注油需x小时可注满油轮的
例5 已知开管注水缸,10分钟可满,拨开底塞,满缸水20 分钟流完,缸内的水流完后,现若管、塞同开,若干时间后,将底塞塞住,又过了2倍的时间才注满水缸,求管塞同开的时间是几分钟?分析: 解:设两管同开x分钟
等量关系:注入量-放出量=缸的容量
依题意得: x=4
答:管塞同开的时间为4分钟x+2x=3x(分钟)x(分钟)解:设再经过x小时水槽里的水恰好等于水槽的等量关系:甲管流进水的水+乙管流出的水 =水槽的 依题意得:
,5例、一个水槽有甲、乙两个水管。甲水管是进水管, 在5小时之内可以把空水槽装满。乙水管是出水管,满槽的水在6小时内可以流完。现水槽内没有水,如果先开甲水管1小时,再把乙水管也打开,再经过几小时5水槽里的水恰好等于水槽容量的? 18答:再经过 小时水槽里的水恰好是水槽容量的例7 一个水池装甲、乙、丙三根水管,单开甲管10小时
可注满水池,单开乙管15小时可注满,单开丙管20
小时可注满。现在三管齐开,中途甲管关闭,结果6
小时把水池注满,问甲管实际开了几个小时?
解:设甲管实际开了x小时
等量关系:甲管x小时的工作量+乙、丙两管同开
6 小时的工作量)= 1
答:甲管实际开了3小时。
依题意得:
x=3等量关系:4天的工作量+改进后(x – 4)工作量= 0.5解:设一共x天可以修完它的一半。
依题意得 ×4+ (x—4)= 0.5
答:一共 天可以修完它的一半。例7分析:x=小结:
1)工程问题或称工作量问题,一定要掌握效率、时间、总量三者之间的关系。 2)部分工作量+部分工作量=总量
解题关键是:审清题意,能用表格法、线段示意图法对题目进行分析。找准相等关系,从而列出方程。
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
