天元初级中学第六章单元图形的初步知识测试卷(解析)
文档属性
| 名称 | 天元初级中学第六章单元图形的初步知识测试卷(解析) |  | |
| 格式 | zip | ||
| 文件大小 | 169.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-12-06 12:22:08 | ||
图片预览




文档简介
天元初级中学七年级数学第六章单元测试卷
班级:___________姓名:___________成绩:___________
一、选择题(每题3分共30分)
1.如图,点O在直线AB上,射线OC平分∠DOB.若∠COB=35°,则∠AOD等于
A.35° B.70° C.110° D.145°
2.一个正方体的平面展开图如图所示,将它折成正方体后,与汉字“岳”相对的面上的汉字是【 】
A.建 B.设 C.和 D.谐
3.下列命题正确的是( )
A、若两个角相等,则这两个角是对顶角 B、若两个角是对顶角,则这两个角不等
C、若两个角是对顶角,则这两个角相等 D、所有同顶点的角都相等
4.下列命题正确的是( )
A、若∠MON+∠NOP=90o,则∠MOP是直角
B、若α与β互为补角,则α与β中必有一个为锐角,另一个为钝角
C、两锐角之和是直角
D、若α与β互为余角,则α与β均为锐角
5.如上图,从A到B有3条路径,最短的路径是③,理由是( )
A.因为③是直的 B.两点确定一条直线
C.两点间距离的定义 D.两点之间,线段最短
6.如果点C在AB上,下列表达式:
①;②;③AC=BC;④中,能表示C是AB中点的有( )
A.1个 B.2个 C.3个 D.4个
7.如图,长方形ABCD沿AE折叠,使D点落在BC边上的F点处,如果∠BAF=60°,则∠DAE等于( )
A.15° B.30° C.45° D.60°
8.如图是一个长方体包装盒,则它的平面展开图是
A. B. C. D.
9.如果∠α=n°,而∠α既有余角,也有补角,那么n的取值范围是( )
A.90°10.如图,甲从A点出发向北偏东70°方向走50m至点B,乙从A出发向南偏西15°方向走80m至点C,则∠BAC的度数是( )
A.85° B.160° C.125° D.105°
二、填空题(每题3分共30分)
11.若∠1+∠2=90°,∠3+∠2=90°,∠1=40°,则∠3=______°,依据是_______。
12.如图3,在直线上顺次取A、B、C、D四点,则AC=______+BC=AD-_____,AC+BD-BC=________.
13.如果∠α=39°31’,∠α的余角∠β =_____,∠α的补角∠γ=_____,∠γ-∠β=___.
14.30.6°=_____°_____′=______′;30°6′=_____′=______°.
15.已知∠1=200,∠2=300,∠3=600,∠4=1500,则∠2是____的余角,_____是∠4的补角.
16.如图是正方体的一种平面展开图,它的每个面上都有一个汉字,那么在原正方体的表面上,与汉字“香”相对的面上的汉字是 .
17.线段AB=8cm,C是AB的中点,D是BC的中点,A、D两点间的距离是_____cm.
18.三棱锥有____个面,它们相交形成了_____条棱, 这些棱相交形成了_____个点.
19.如图是正方体的平面展开图,每个面上标有汉字组成的三个词,分别是兰州人引以自豪的三个词(一本书,一条河,一碗面),在正方体上与“读”字相对的面上的字是_______.
20.要把一个正方体分割成8个小正方体,至少需要切3刀,因为这8个小正方体都只有三个面现成的,其它三个面必须用刀切3次才能切出来,那么,要把一个正方体分割成27个小正方体,至少需要要刀切 次,分割成64个小正方体,至少需要用刀切 次。
三、解答题(第21~23每题4分,第24~25每题8分,笫26题12分,第27~28每题10分,共60分)
21.计算:49°38′+ 66°22′;
22.计算:180°- 79°19′;
23.计算:182°36′÷4.
24.一个角的余角比这个角 少40°,求这个角的度数.
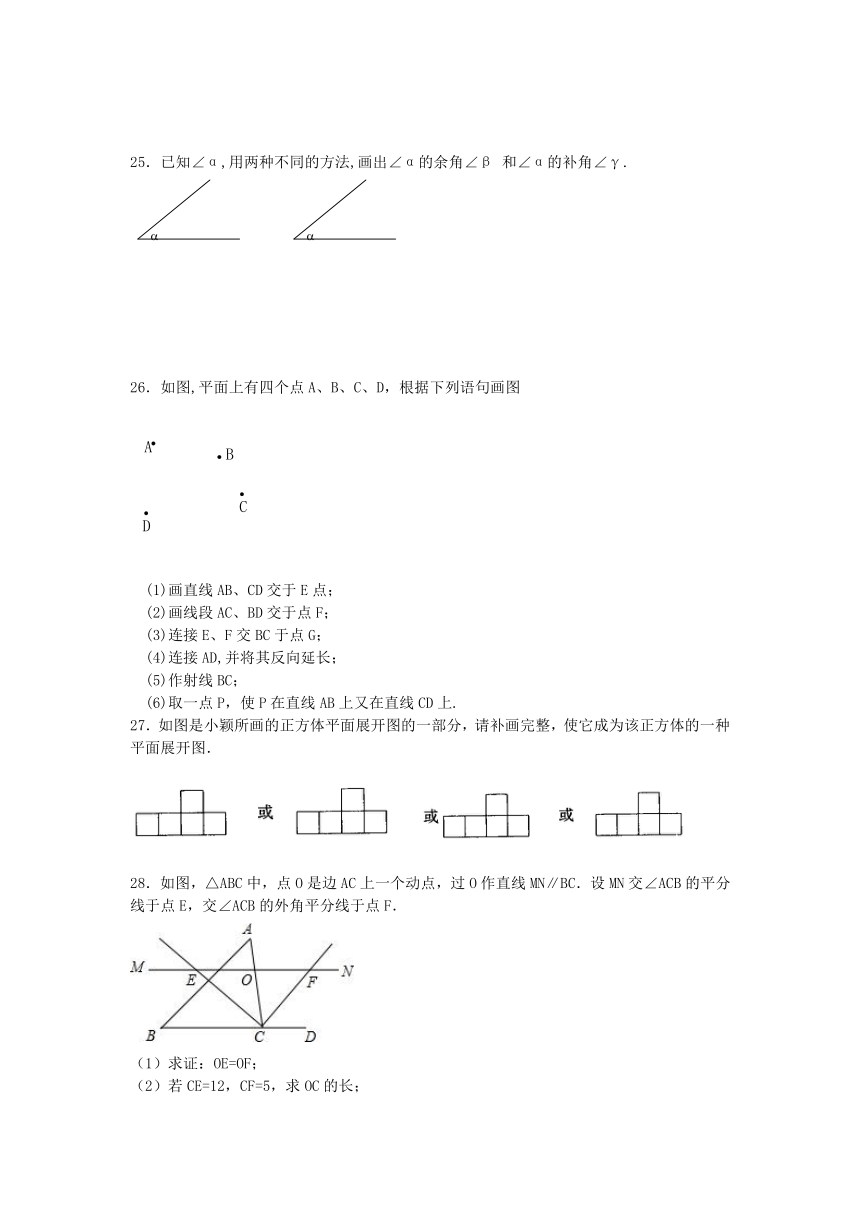
25.已知∠α,用两种不同的方法,画出∠α的余角∠β 和∠α的补角∠γ.
26.如图,平面上有四个点A、B、C、D,根据下列语句画图
(1)画直线AB、CD交于E点;
(2)画线段AC、BD交于点F;
(3)连接E、F交BC于点G;
(4)连接AD,并将其反向延长;
(5)作射线BC;
(6)取一点P,使P在直线AB上又在直线CD上.
27.如图是小颖所画的正方体平面展开图的一部分,请补画完整,使它成为该正方体的一种平面展开图.
28.如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
参考答案
1.C
【解析】
试题分析:∵射线OC平分∠DOB,∴∠BOD=2∠BOC。
∵∠COB=35°,∴∠DOB=70°。
∴∠AOD=180°﹣70°=110°。
故选C。
2.C。
【解析】正方体的表面展开图,相对的面之间一定相隔一个正方形,因此,
“和”与“岳”是相对面,“建”与“阳”是相对面,“谐”与“设”是相对面。故选C。
3.C
【解析】本题考查的是对顶角
根据对顶角相等,且对顶角的两边互为反向延长线进行判断.
所有的直角都相等,但不一定是对顶角,故本选项错误;
若两个角是对顶角,则这两个角必然相等,故本选项错误;
若两个角是对顶角,则这两个角相等,正确;
所有同顶点的角都相等,没有说明两边互为反向延长线,故本选项错误,
故选C。
4.D
【解析】本题考查的是余角、补角的性质
根据和为的两个角互为余角,和为的两个角互为补角,即可得到结果。
A、若∠MON+∠NOP=90o,则∠MOP必是锐角,故本选项错误;
B、若α与β互为补角,可能两个角均为直角,故本选项错误;
C、两锐角之和不一定是直角,故本选项错误;
D、若α与β互为余角,则α与β均为锐角,正确;
故选D。
5.D
【解析】本题考查的是最短路径问题
根据“两点之间,线段最短”的特征即可得到最短路径.
走路径③,是因为路径③是一条直线,根据“两点之间,线段最短”.故选D.
6.C
【解析】本题考查的是线段的中点
根据题意,画出图形,观察图形,一一分析选项,排除错误答案.
若C是线段AB的中点,则,
而,可是线段上的任意一点,
∴表示是线段的中点的有①②③共3个.
故选C.
7.A
【解析】本题考查的是翻折变换及矩形的性质
先求得∠DAF=30°,又根据AF是AD折叠得到的(翻折前后的对应角相等),可知∠DAE=∠EAF=15°.
∵∠BAF=60°,
∴∠DAF=30°,
又∵AF是AD折叠得到的,
∴△ADE≌△AFE,
∴∠DAE=∠EAF∠DAF=15°.
故选A。
8.A
【解析】
试题分析:长方体的四个侧面中,有两个相对面的小长方形,另两个是相对面的大长方形,B、C中两个小的与两个大的相邻,错误,D中底面不符合,只有A符合。故选A。
9.B
【解析】本题考查的是余角、补角
根据和为的两个角互为余角,和为的两个角互为补角,即可得到结果。
∠α既有余角,也有补角,那么n的取值范围是,故选B。
10.C
【解析】本题考查的是方位角
根据方位角的概念结合图形解答.
由题意得,∠,故选C。
11.40°,同角的余角相等
【解析】本他考查的是同角的余角相等
先由∠1的度数求出∠2的度数,即可得到∠3的度数.
∠1+∠2,∠2∠1,
∠3+∠2,∠3∠1,
依据是同角的余角相等。
12.AB,CD,AD
【解析】本题考查了比较线段长短的知识
从图上可以直观的看出各线段的关系.
由图可知各线段的关系为:
13.50°29′,140°31′,90°
【解析】本题考查的是余角、补角
根据和为的两个角互为余角,和为的两个角互为补角,即可得到结果。
∠α的余角∠β,
∠α的余角∠γ,
则∠γ-∠β
14.30,36,1836;1806,30.1
【解析】本题考查的是度、分、秒转化运算
进行度、分、秒转化运算,注意以60为进制.
;.
15.∠3,∠2
【解析】本题考查的是余角、补角
根据和为的两个角互为余角,和为的两个角互为补角,即可得到结果。
∠2∠3,∠2是∠3的余角,
∠2∠4,∠2是∠4的补角。
16.泉
【解析】
试题分析:正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点,得
“力”与“城”是相对面,“香”与“泉”是相对面,“魅”与“都”是相对面。
∴与汉字“香”相对的面上的汉字是泉。
17.6
【解析】本题考查的是两点间的距离问题
可依据题意作出简单的图形,进而结合图形求解线段的长度.
如图
∵AB=8cm,C是AB的中点,∴AC=4cm,
又D是BC的中点,∴,
18.4;6;4
【解析】本题考查了三棱锥的特征
根据三棱锥的顶点、棱及面的特点作答.
三棱锥有4个面,它们相交形成了6条棱,这些棱相交形成了4个点.
19.面
【解析】本题考查的是正方体的平面展开图
正方体的平面展开图中,相对面的特点是之间一定相隔一个正方形,据此作答.
正方体的平面展开图中,相对面的特点是之间一定相隔一个正方形,所以在此正方体上与“读”字相对的面上的汉字是“面”.
20.6;9
【解析】
试题分析:∵27=3×3×3 ,2刀可切3段,从前,上,侧三个方向切每面2刀可得27个小正方体,
∴要把一个正方体分割成27个小正方体,至少需要要刀切2×3=6次。
∵64=4×4×4 ,3刀可切4段,从前,上,侧三个方向切每面3刀可得64个小正方体,
∴要把一个正方体分割成64个小正方体,至少需要要刀切3×3=9次。
21.116°
【解析】本题考查的是度、分的加法计算
两个度数相加,度与度,分与分对应相加,分的结果若满60,则转化为度.
22.100°41′
【解析】本题考查的是度、分的减法计算
两个度数相减,度与度,分与分对应相减,若不够减的则化即可.
23.45°39′
【解析】本题考查的是度、分的除法计算
先把度、分部分分别除以4,小数部分则转化为下一级单位,注意要乘以进率60.
24.
【解析】本题考查了余角的定义
设这个角为∠A,则这个余角的为90°∠A,根据题意解方程即可.
设这个角为∠A,则这个余角的为90°∠A,由题意得
∠A(90°∠A),解得∠A
25.见解析
【解析】本题考查了余角和补角的定义
(1)作∠α的余角:①在顶点处作一边的垂线,这条垂线与另一边组成的锐角为∠α的余角;
②在顶点处作另一边的垂线,与一边组成的锐角即为∠α的余角.
(2)作∠α的补角:①过∠α的一边做其反向延长线,延长线与另一边所组成的角为∠α的补角;
②过另一条边作其反向延长线,延长线与一边所组成的钝角即为∠α的补角.
∠α的余角如图(1)、(2),∠α的补角如图(3)、(4):
26.见解析
【解析】本题考查的是平面图形的基本作图
根据直线向两方无限延伸;射线向一方无限延伸;线段有两个端点再结合题意画出图形即可,要注意作图的规范性。
如图所示:
27.见解析
【解析】本题主要考查了正方体的展开图
根据正方体的展开图特点补全即可,答案不唯一.
如图所示:、、、。
28.解:(1)证明:如图,∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,
∴∠2=∠5,4=∠6。
∵MN∥BC,∴∠1=∠5,3=∠6。
∴∠1=∠2,∠3=∠4。∴EO=CO,FO=CO。
∴OE=OF。
(2)∵∠2=∠5,∠4=∠6,∴∠2+∠4=∠5+∠6=90°。
∵CE=12,CF=5,∴。
∴OC=EF=6.5。
(3)当点O在边AC上运动到AC中点时,四边形AECF是矩形。理由如下:
当O为AC的中点时,AO=CO,
∵EO=FO,∴四边形AECF是平行四边形。
∵∠ECF=90°,∴平行四边形AECF是矩形。
【解析】(1)根据平行线的性质以及角平分线的性质得出∠1=∠2,∠3=∠4,进而得出答案。
(2)根据已知得出∠2+∠4=∠5+∠6=90°,进而利用勾股定理求出EF的长,即可根据直角三角形斜边上的中线性质得出CO的长。
(3)根据平行四边形的判定以及矩形的判定得出即可。
班级:___________姓名:___________成绩:___________
一、选择题(每题3分共30分)
1.如图,点O在直线AB上,射线OC平分∠DOB.若∠COB=35°,则∠AOD等于
A.35° B.70° C.110° D.145°
2.一个正方体的平面展开图如图所示,将它折成正方体后,与汉字“岳”相对的面上的汉字是【 】
A.建 B.设 C.和 D.谐
3.下列命题正确的是( )
A、若两个角相等,则这两个角是对顶角 B、若两个角是对顶角,则这两个角不等
C、若两个角是对顶角,则这两个角相等 D、所有同顶点的角都相等
4.下列命题正确的是( )
A、若∠MON+∠NOP=90o,则∠MOP是直角
B、若α与β互为补角,则α与β中必有一个为锐角,另一个为钝角
C、两锐角之和是直角
D、若α与β互为余角,则α与β均为锐角
5.如上图,从A到B有3条路径,最短的路径是③,理由是( )
A.因为③是直的 B.两点确定一条直线
C.两点间距离的定义 D.两点之间,线段最短
6.如果点C在AB上,下列表达式:
①;②;③AC=BC;④中,能表示C是AB中点的有( )
A.1个 B.2个 C.3个 D.4个
7.如图,长方形ABCD沿AE折叠,使D点落在BC边上的F点处,如果∠BAF=60°,则∠DAE等于( )
A.15° B.30° C.45° D.60°
8.如图是一个长方体包装盒,则它的平面展开图是
A. B. C. D.
9.如果∠α=n°,而∠α既有余角,也有补角,那么n的取值范围是( )
A.90°
A.85° B.160° C.125° D.105°
二、填空题(每题3分共30分)
11.若∠1+∠2=90°,∠3+∠2=90°,∠1=40°,则∠3=______°,依据是_______。
12.如图3,在直线上顺次取A、B、C、D四点,则AC=______+BC=AD-_____,AC+BD-BC=________.
13.如果∠α=39°31’,∠α的余角∠β =_____,∠α的补角∠γ=_____,∠γ-∠β=___.
14.30.6°=_____°_____′=______′;30°6′=_____′=______°.
15.已知∠1=200,∠2=300,∠3=600,∠4=1500,则∠2是____的余角,_____是∠4的补角.
16.如图是正方体的一种平面展开图,它的每个面上都有一个汉字,那么在原正方体的表面上,与汉字“香”相对的面上的汉字是 .
17.线段AB=8cm,C是AB的中点,D是BC的中点,A、D两点间的距离是_____cm.
18.三棱锥有____个面,它们相交形成了_____条棱, 这些棱相交形成了_____个点.
19.如图是正方体的平面展开图,每个面上标有汉字组成的三个词,分别是兰州人引以自豪的三个词(一本书,一条河,一碗面),在正方体上与“读”字相对的面上的字是_______.
20.要把一个正方体分割成8个小正方体,至少需要切3刀,因为这8个小正方体都只有三个面现成的,其它三个面必须用刀切3次才能切出来,那么,要把一个正方体分割成27个小正方体,至少需要要刀切 次,分割成64个小正方体,至少需要用刀切 次。
三、解答题(第21~23每题4分,第24~25每题8分,笫26题12分,第27~28每题10分,共60分)
21.计算:49°38′+ 66°22′;
22.计算:180°- 79°19′;
23.计算:182°36′÷4.
24.一个角的余角比这个角 少40°,求这个角的度数.
25.已知∠α,用两种不同的方法,画出∠α的余角∠β 和∠α的补角∠γ.
26.如图,平面上有四个点A、B、C、D,根据下列语句画图
(1)画直线AB、CD交于E点;
(2)画线段AC、BD交于点F;
(3)连接E、F交BC于点G;
(4)连接AD,并将其反向延长;
(5)作射线BC;
(6)取一点P,使P在直线AB上又在直线CD上.
27.如图是小颖所画的正方体平面展开图的一部分,请补画完整,使它成为该正方体的一种平面展开图.
28.如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
参考答案
1.C
【解析】
试题分析:∵射线OC平分∠DOB,∴∠BOD=2∠BOC。
∵∠COB=35°,∴∠DOB=70°。
∴∠AOD=180°﹣70°=110°。
故选C。
2.C。
【解析】正方体的表面展开图,相对的面之间一定相隔一个正方形,因此,
“和”与“岳”是相对面,“建”与“阳”是相对面,“谐”与“设”是相对面。故选C。
3.C
【解析】本题考查的是对顶角
根据对顶角相等,且对顶角的两边互为反向延长线进行判断.
所有的直角都相等,但不一定是对顶角,故本选项错误;
若两个角是对顶角,则这两个角必然相等,故本选项错误;
若两个角是对顶角,则这两个角相等,正确;
所有同顶点的角都相等,没有说明两边互为反向延长线,故本选项错误,
故选C。
4.D
【解析】本题考查的是余角、补角的性质
根据和为的两个角互为余角,和为的两个角互为补角,即可得到结果。
A、若∠MON+∠NOP=90o,则∠MOP必是锐角,故本选项错误;
B、若α与β互为补角,可能两个角均为直角,故本选项错误;
C、两锐角之和不一定是直角,故本选项错误;
D、若α与β互为余角,则α与β均为锐角,正确;
故选D。
5.D
【解析】本题考查的是最短路径问题
根据“两点之间,线段最短”的特征即可得到最短路径.
走路径③,是因为路径③是一条直线,根据“两点之间,线段最短”.故选D.
6.C
【解析】本题考查的是线段的中点
根据题意,画出图形,观察图形,一一分析选项,排除错误答案.
若C是线段AB的中点,则,
而,可是线段上的任意一点,
∴表示是线段的中点的有①②③共3个.
故选C.
7.A
【解析】本题考查的是翻折变换及矩形的性质
先求得∠DAF=30°,又根据AF是AD折叠得到的(翻折前后的对应角相等),可知∠DAE=∠EAF=15°.
∵∠BAF=60°,
∴∠DAF=30°,
又∵AF是AD折叠得到的,
∴△ADE≌△AFE,
∴∠DAE=∠EAF∠DAF=15°.
故选A。
8.A
【解析】
试题分析:长方体的四个侧面中,有两个相对面的小长方形,另两个是相对面的大长方形,B、C中两个小的与两个大的相邻,错误,D中底面不符合,只有A符合。故选A。
9.B
【解析】本题考查的是余角、补角
根据和为的两个角互为余角,和为的两个角互为补角,即可得到结果。
∠α既有余角,也有补角,那么n的取值范围是,故选B。
10.C
【解析】本题考查的是方位角
根据方位角的概念结合图形解答.
由题意得,∠,故选C。
11.40°,同角的余角相等
【解析】本他考查的是同角的余角相等
先由∠1的度数求出∠2的度数,即可得到∠3的度数.
∠1+∠2,∠2∠1,
∠3+∠2,∠3∠1,
依据是同角的余角相等。
12.AB,CD,AD
【解析】本题考查了比较线段长短的知识
从图上可以直观的看出各线段的关系.
由图可知各线段的关系为:
13.50°29′,140°31′,90°
【解析】本题考查的是余角、补角
根据和为的两个角互为余角,和为的两个角互为补角,即可得到结果。
∠α的余角∠β,
∠α的余角∠γ,
则∠γ-∠β
14.30,36,1836;1806,30.1
【解析】本题考查的是度、分、秒转化运算
进行度、分、秒转化运算,注意以60为进制.
;.
15.∠3,∠2
【解析】本题考查的是余角、补角
根据和为的两个角互为余角,和为的两个角互为补角,即可得到结果。
∠2∠3,∠2是∠3的余角,
∠2∠4,∠2是∠4的补角。
16.泉
【解析】
试题分析:正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点,得
“力”与“城”是相对面,“香”与“泉”是相对面,“魅”与“都”是相对面。
∴与汉字“香”相对的面上的汉字是泉。
17.6
【解析】本题考查的是两点间的距离问题
可依据题意作出简单的图形,进而结合图形求解线段的长度.
如图
∵AB=8cm,C是AB的中点,∴AC=4cm,
又D是BC的中点,∴,
18.4;6;4
【解析】本题考查了三棱锥的特征
根据三棱锥的顶点、棱及面的特点作答.
三棱锥有4个面,它们相交形成了6条棱,这些棱相交形成了4个点.
19.面
【解析】本题考查的是正方体的平面展开图
正方体的平面展开图中,相对面的特点是之间一定相隔一个正方形,据此作答.
正方体的平面展开图中,相对面的特点是之间一定相隔一个正方形,所以在此正方体上与“读”字相对的面上的汉字是“面”.
20.6;9
【解析】
试题分析:∵27=3×3×3 ,2刀可切3段,从前,上,侧三个方向切每面2刀可得27个小正方体,
∴要把一个正方体分割成27个小正方体,至少需要要刀切2×3=6次。
∵64=4×4×4 ,3刀可切4段,从前,上,侧三个方向切每面3刀可得64个小正方体,
∴要把一个正方体分割成64个小正方体,至少需要要刀切3×3=9次。
21.116°
【解析】本题考查的是度、分的加法计算
两个度数相加,度与度,分与分对应相加,分的结果若满60,则转化为度.
22.100°41′
【解析】本题考查的是度、分的减法计算
两个度数相减,度与度,分与分对应相减,若不够减的则化即可.
23.45°39′
【解析】本题考查的是度、分的除法计算
先把度、分部分分别除以4,小数部分则转化为下一级单位,注意要乘以进率60.
24.
【解析】本题考查了余角的定义
设这个角为∠A,则这个余角的为90°∠A,根据题意解方程即可.
设这个角为∠A,则这个余角的为90°∠A,由题意得
∠A(90°∠A),解得∠A
25.见解析
【解析】本题考查了余角和补角的定义
(1)作∠α的余角:①在顶点处作一边的垂线,这条垂线与另一边组成的锐角为∠α的余角;
②在顶点处作另一边的垂线,与一边组成的锐角即为∠α的余角.
(2)作∠α的补角:①过∠α的一边做其反向延长线,延长线与另一边所组成的角为∠α的补角;
②过另一条边作其反向延长线,延长线与一边所组成的钝角即为∠α的补角.
∠α的余角如图(1)、(2),∠α的补角如图(3)、(4):
26.见解析
【解析】本题考查的是平面图形的基本作图
根据直线向两方无限延伸;射线向一方无限延伸;线段有两个端点再结合题意画出图形即可,要注意作图的规范性。
如图所示:
27.见解析
【解析】本题主要考查了正方体的展开图
根据正方体的展开图特点补全即可,答案不唯一.
如图所示:、、、。
28.解:(1)证明:如图,∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,
∴∠2=∠5,4=∠6。
∵MN∥BC,∴∠1=∠5,3=∠6。
∴∠1=∠2,∠3=∠4。∴EO=CO,FO=CO。
∴OE=OF。
(2)∵∠2=∠5,∠4=∠6,∴∠2+∠4=∠5+∠6=90°。
∵CE=12,CF=5,∴。
∴OC=EF=6.5。
(3)当点O在边AC上运动到AC中点时,四边形AECF是矩形。理由如下:
当O为AC的中点时,AO=CO,
∵EO=FO,∴四边形AECF是平行四边形。
∵∠ECF=90°,∴平行四边形AECF是矩形。
【解析】(1)根据平行线的性质以及角平分线的性质得出∠1=∠2,∠3=∠4,进而得出答案。
(2)根据已知得出∠2+∠4=∠5+∠6=90°,进而利用勾股定理求出EF的长,即可根据直角三角形斜边上的中线性质得出CO的长。
(3)根据平行四边形的判定以及矩形的判定得出即可。
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
