5.2函数(2）

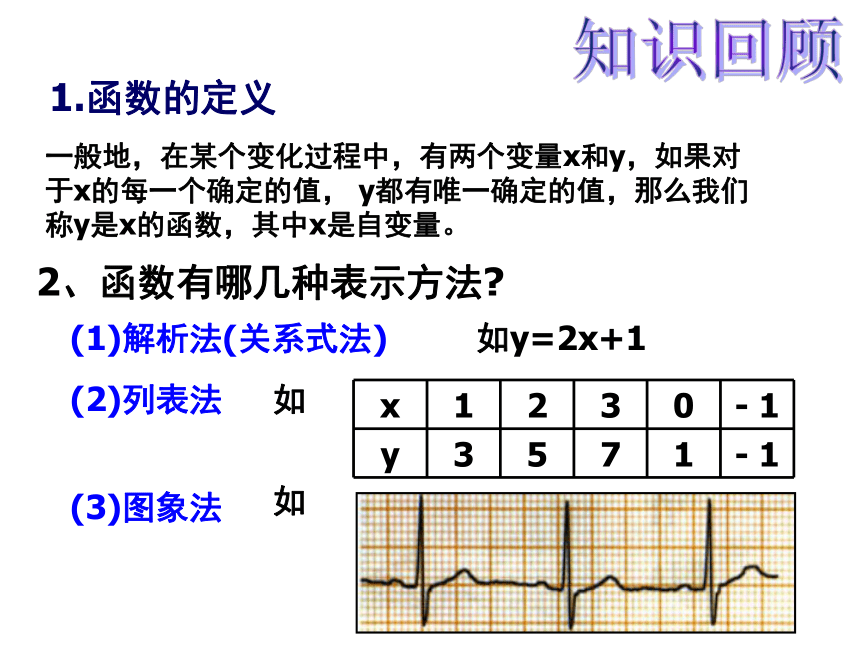
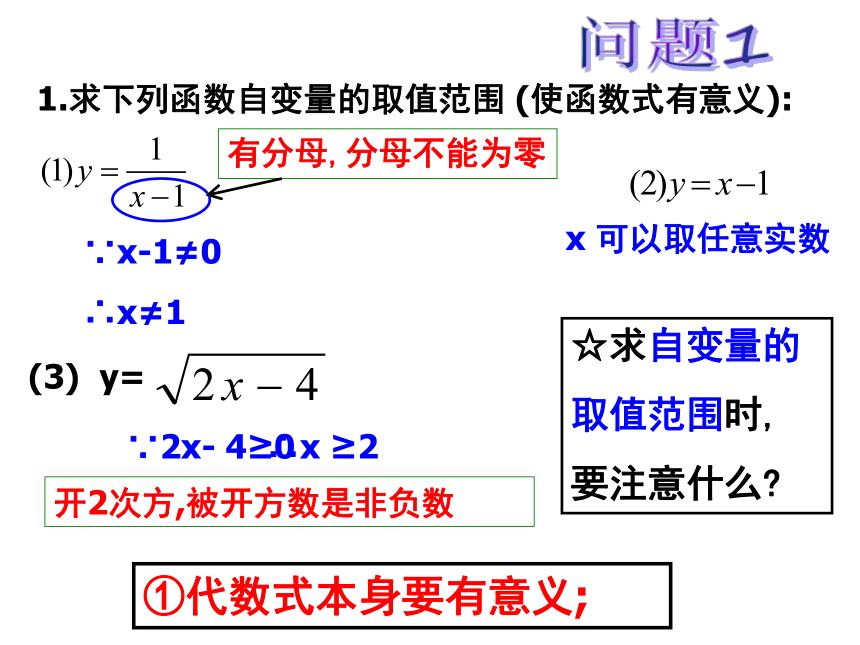
课件21张PPT。泰顺六中 翁怀新2013年12月5日5.2 函数（2）2、函数有哪几种表示方法? (1)解析法(关系式法)如y=2x+1 (2)列表法 如 (3)图象法 如 1.函数的定义 一般地，在某个变化过程中，有两个变量x和y，如果对于x的每一个确定的值， y都有唯一确定的值，那么我们称y是x的函数，其中x是自变量。 知识回顾1.求下列函数自变量的取值范围 (使函数式有意义): 问题1有分母,分母不能为零∵2x- 4≥0
∴x ≥2
开2次方,被开方数是非负数☆求自变量的
取值范围时,
要注意什么?∵x-1≠0
∴x≠1
x 可以取任意实数①代数式本身要有意义; (4)儿童节的时候，每人发2颗糖果，总人数x与总发的糖果数y的函数关系式为____________,其中人数x的取值范围是___________。 y= 2x x为正整数 问题2②符合实际意义. ☆求自变量的
取值范围时,
还要注意什么?求下列函数自变量的取值范围（使函数式有意义）：试一试例1、等腰三角形ABC的周长为10，底边BC长为y，腰AB长为x，求：（1）y关于x的函数解析式；
（2）自变量x的取值范围；
（3）腰长AB=3时，底边的长 解： （1）由三角形的周长为10，得2 x+ y=10∴ y=10-2x（2） ∵x，y是三角形的边长为10，∴ x ＞0 ，y ＞0 2 x ＞ y（代数式要有意义，并且三角形的两边之和大于第三边）解得 2.5 ＜ x ＜ 5（3）当AB=3时，即x=3时，y=10-2× 3=4.所以当腰AB=3时，底边BC长为4.例1、等腰三角形ABC的周长为10，底边BC长为y，腰AB长为x，求：解： （1）由三角形的周长为10，得2 x+ y=10∴ y=10-2x（2） ∵x，y是三角形的边长为10，∴ x ＞0 ，y ＞0 2 x ＞ y（代数式要有意义，并且三角形的两边之大于第三边和）解得 2.5 ＜ x ＜ 5（3）当AB=3时，即x=3时，y=10-2× 3=4.所以当腰AB=3时，底边BC长为4.想一想当x=6时,y=10-2x的值是多少?对本例有意义吗?当x=2呢? 例1、等腰三角形ABC的周长为10，底边BC长为y，腰AB长为x，求：想一想当x=6时,y=10-2x的值是多少?对本例有意义吗?当x=2呢? 解：当x=6时,y=10-2x=10-2 × 6=-2.不符合实际意义，即无意义.当x=2,y=10-2x=10-2 × 2=6,即2x ＜ y.不符合‘三角形的两边之和大于第三边’所以无意义.1、设等腰三角形顶角度数为y，底角度数为x，则（ ）
A、y＝180－2x（x可为全体实数）
B、y＝180－2x（0≤x≤90）
C、y＝180－ 2x （0＜x＜90）
D、C2、如果一个圆筒形水管的外径是R，内径是6，它的横截面积S关于外径R的函数关系式为S＝π（R2－36），那么R的取值范围为（ ）
A、全体实数 B、全体正实数
C、全体非负实数 D、所有大于6的实数D练一练 3、用总长为60cm的铁丝围成长方形，如果长方形的一边长为 a（cm），面积为 S （cm2）。
（1）写出 S关于a 的函数关系式。及自变量a的取值范围。
（2）利用所写的关系式计算当a=12时，S的值是多少？a(30-a)S= a(30-a)解:(1)（0(1) 完成下表
y =100－0.2x巩固练习P148解: ∵设AE= x ， ∴ BE=1- x 由题意可得△AHE与△BEF与△CFG
与△GDH的4个三角形的面积都相等。∴S正方形EFGH=S正方形ABCD -S△AEH（0 ＜ x ＜ 1）1.求函数解析式：
可以先得到函数与自变量之间的等式,然后用自变量的代数式表示函数；

2.求函数自变量取值范围的两个依据：
(1)要使代数式本身有意义．
(2)对于反映实际问题的函数关系，应使实际问题有意义．
3.求另一变量值的方法：
跟求代数式的值的方法一样就是把所给出的变量的值代入函数解析式中，
即可求出相应的函数值．4.重要数学思想与方法：转化、数形结合. 课堂小结如图：每个图形都是由若干棋子围成的正方形图案，图案的每条边（包括两个顶点）上都有n(n≥2)个棋子，设每个图案的棋子总数为S。
图中棋子的排列有什么规律？与之间能用函数解析式表示吗？自变量的取值范围是什么?n=2s =4s =16s =12s =8n=3n=4n=5探究活动S与 n的函数关系式:S=4n -4n的取值范围:n>1的整数 如图是由若干个棋子围成的形如三角形的图案,每条边有n个棋子,每个图案棋子的总数是s，按此规律，你能摆出第四个、第五个图案吗？当每条边有n个棋子时,你能写出每个图案总数s与每边棋子个数n之间的关系式吗？n的取值范围是什么？ S与 n的函数关系式:S=3n -3
n的取值范围:n>1的整数 拓展提高1 等腰直角△ABC的直角边长与正方形MNPQ的边长均为10 cm，AC与MN在同一直线上，开始时A点与M点重合，让△ABC向右运动，最后A点与N点重合．试写出△ABC运动过程中，重叠部分面积ycm2与MA长度x cm之间的函数关系式．拓展提高2y与 x的函数关系式:
(0＜ x ＜10)再见作业本（2）中的5.2（2）布置作业：再见布置作业：作业本（2）中的5.2（2）