7.3线段的长短比较2[上学期]

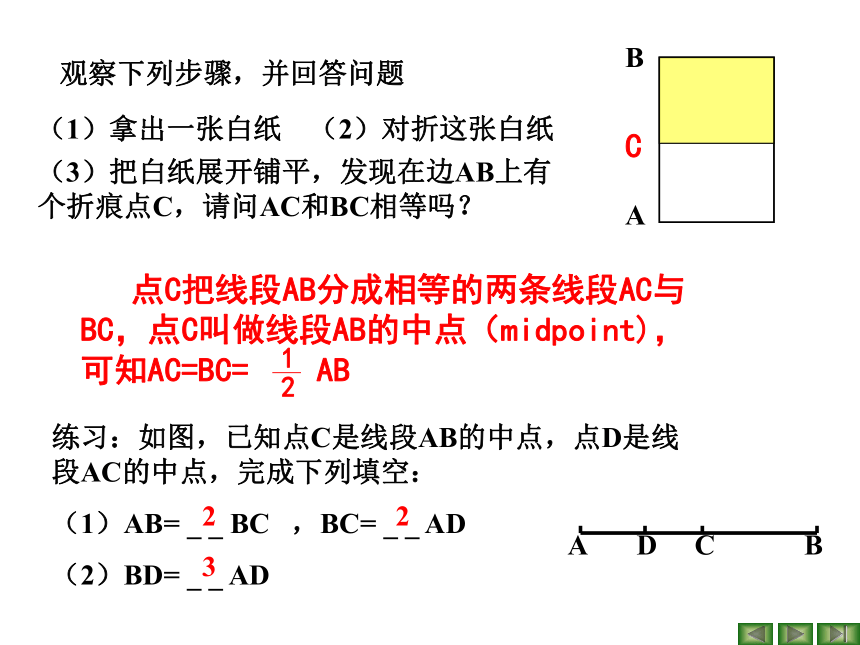
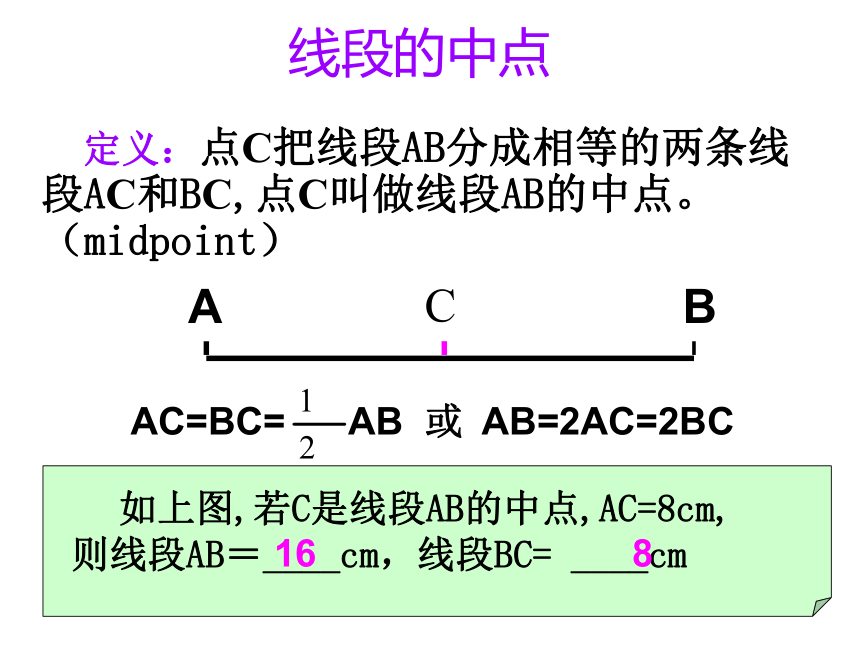
课件17张PPT。数学名言 数缺形时少直观，形缺数时少入微华罗庚7.3 线段的长短比较 2 　观察下列步骤，并回答问题（1）拿出一张白纸（2）对折这张白纸（3）把白纸展开铺平，发现在边AB上有个折痕点C，请问AC和BC相等吗？C223线段的中点 定义：点C把线段AB分成相等的两条线段AC和BC,点C叫做线段AB的中点。（midpoint）C 如上图,若C是线段AB的中点,AC=8cm,
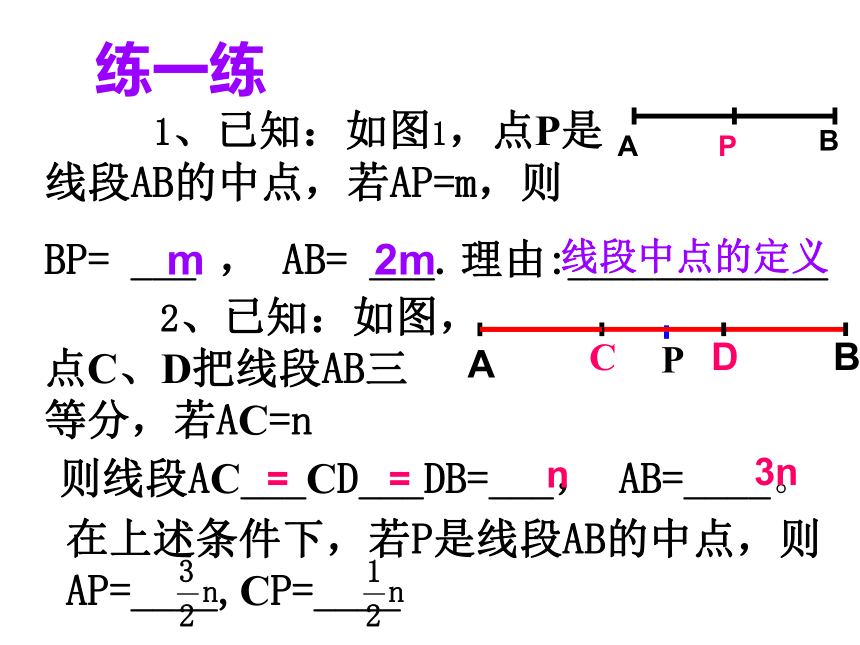
则线段AB＝____cm，线段BC= ____cm168AC=BC= ABAB=2AC=2BC或练一练 1、已知：如图1，点P是线段AB的中点，若AP=m，则
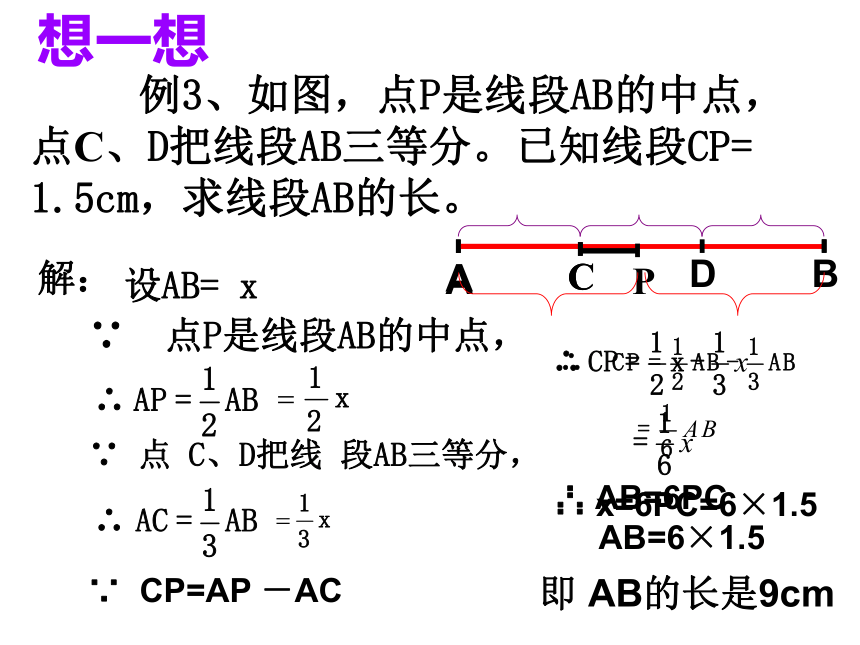
BP= ___ ， AB= ___.理由:____________m2m线段中点的定义 2、已知：如图，点C、D把线段AB三等分，若AC=n则线段AC___CD___DB=___， AB=____。在上述条件下，若P是线段AB的中点，则AP=____,CP=____==n3n想一想 例3、如图，点P是线段AB的中点，点C、D把线段AB三等分。已知线段CP=1.5cm，求线段AB的长。ABA解：∵ 点P是线段AB的中点，∵ 点 C、D把线 段AB三等分，∵ CP=AP －AC即 AB的长是9cm∴ AB=6PC
AB=6×1.5　　　设AB= x∴ x=6PC=6×1.5　　　　一天，小丑鱼和它的朋友在海里游玩，碰到了凶恶的鲨鱼NICK，小丑 鱼和它的朋友为了逃到安全地带，有三条路可以选择，你猜它们将选择哪条路？安全的家 在所有连结两点的线中，线段最短. 简单说成: 两点之间，线段最短。线段的基本性质:小明家学校（1）（2）(2)两点之间，线段最短应用 如图，从小明家到学校共有三条路，小明为了尽快到学校，应选择第 ＿＿条路，用数学知识解释为_____________．议一议:
在我们生活中有多少利用这条性质的例子?（3）我们把连结两点间线段的长度叫这两点间的距离。练一练错两点之间线段最短(1)判断:两点之间的距离是指两点之间的线段。 ( )(2)如图:这是A、B两地之间的公路，在公路工程改造计划时，为使A、B两地行程最短，应如何设计线路？在图中画出。你的理由是
1、下列说法正确的是（ ）
A、连结两点的线段叫做两点间的距离
B、两点间的连线的长度，叫做两点间的距离
C、连结两点的直线的长度，叫做两点的距离
D、连结两点的线段的长度，叫做两点间的距离D练一练问：若要在西湖风景区建造一个消费场所，为了方便游客，要求是到图中四个红色的旅游区的距离之和最短，请问应该建造在何处？如图，线段AB与线段CD的交点E为所求的点，即消费场所建在E点位置最合适。解：练一练 1、如图，点C、B、M在线段AN上，C为AB中点，M为BN中点，AC=2cm ，BN=8cm，求CM的长。AAN 2、已知线段AB=a ，延长BA至点C使 AC= 。点D为线段BC的中点。
（1）求CD的长
（2）若AD= 3 cm ，求AB的长CDa练习1、M是线段AB上的一点，其中不能判定点M是线段AB中点的是（ ）
A、AM+BM=AB B、AM=BM
C、AB=2BM2、线段AB=6厘米，点C在直线AB上，且BC=3厘米，则线段AC的长为（ ）
A、3厘米 B、9厘米
C、3厘米或9厘米Ac思维拓展 如图，有一只蚂蚁，沿长方体的表面一端爬到另一端，怎样画出最短的路线？今天你收获了吗？相信你肯定是收获了，因为老师看到了许多同学很想起来总结一下！小结与作业通过这节课的学习，你学到了些什么？
作业：作业本（1） P37