7.6余角和补角[上学期]
图片预览

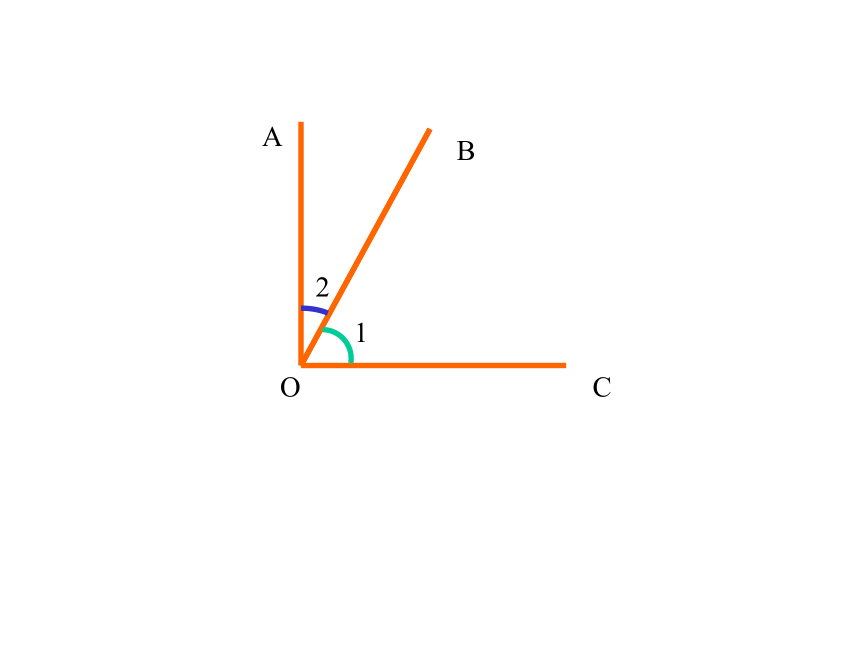



文档简介
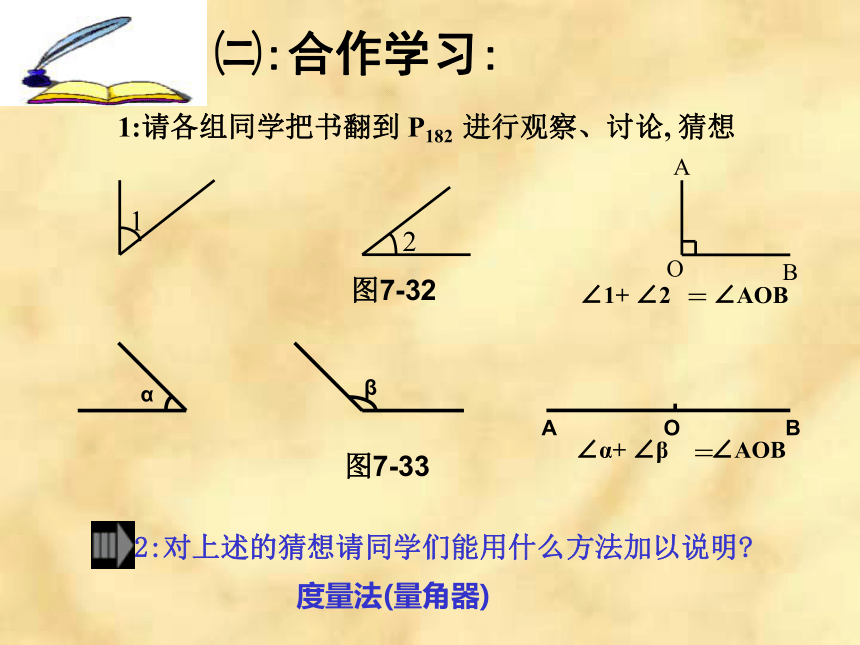
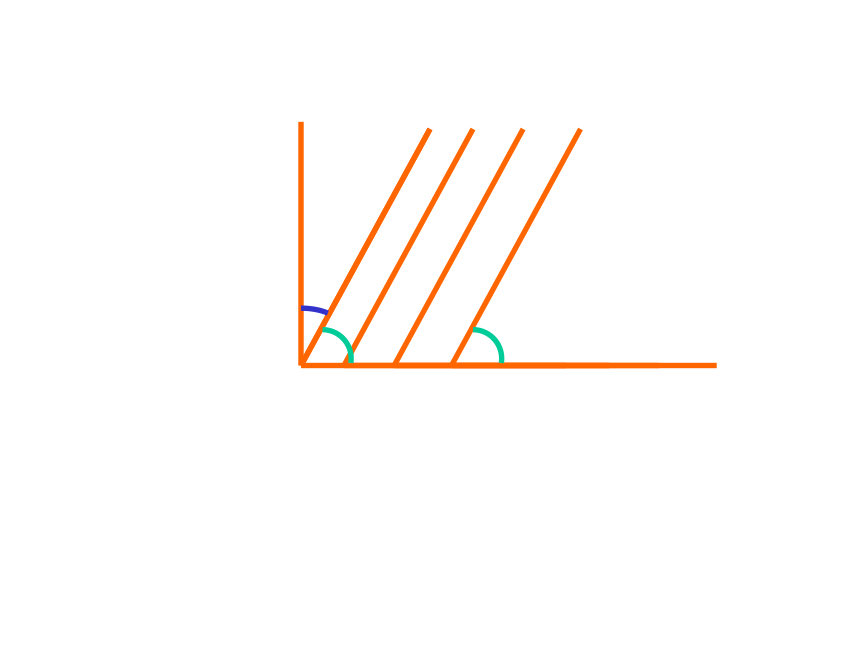
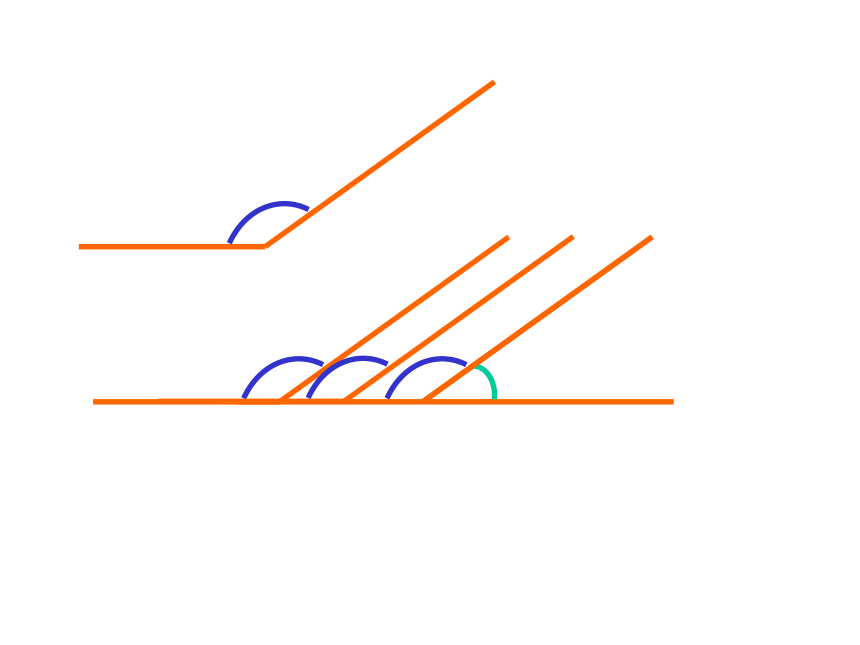
课件27张PPT。7?6 余角和补角一:教学目标:1:了解补角和余角的概念知识目标:2:理解同角(或等角)的余角(或补角)相等能力目标:二:教学重点:了解在解决实际问题中的一些简单应用教学难点:补角和余角的概念和性质㈠:创设情景 , 引出课题:三:教学过程:关于补角和余角的概念和性质的应用常常需要说明理由或综合运用代数知识是本节教学难点㈡:合作学习:1:请各组同学把书翻到 P182 进行观察、讨论, 猜想=∠1+ ∠2 ∠AOB图7-32图7-33度量法(量角器)2:对上述的猜想请同学们能用什么方法加以说明?∠α+ ∠β ∠AOB=ABOC12互为余角
如果两个角的和是一个直角,那么这两个角叫做互为余角,其中一个角是另一个角的余角。
互为补角
如果两个角的和是一个平角,那么这两个角叫做互为补角。其中一个角是另一个角的补角。
互为余角
如果 的和是一个 ,那么这两个角叫做 余角,其中一个角是 的余角。
互为补角
如果 的和是一个 ,那么这两个角叫做 补角,其中一个角是 的补角。
两个角直角互为另一个角两个角互为另一个角平角小结:∠1 +∠2=90o①互余、互补是指两个角 若两个角的和是平角,则就说这两个角互为补角,其中一个角是另一个角的补角定 义互为余角 (互余) 若两个锐角和是一个直角,则就说这两个角互为余角,其中一个角是另一个角的余角 ②互余、互补只跟角度的大小有关与位置无关互为补角 (互补)∠α+∠β=180o数量关系注意点概 念若∠1 + ∠2 =180 °,
则 .( )
若∠1和∠2互补,
则 .( )
若∠3 + ∠4 =90 °,则 .( )
若∠3和∠4互余,
则 .( )312∠1和∠2互补互补定义∠1 + ∠2 =180 °互补定义∠3和∠4互余互余定义∠3 + ∠4 =90 °互余定义㈢:快速练一练 1:如图,已知∠1=42o, ∠2=138o, ∠3=48o,问图中有没有互余或互补的角?若有,请把它们写出来,并说明理由。 2: 如图, 点O为直线AB上一点, ∠AOB=Rt ∠, OD是∠BOC内的一条射线。图中有哪角是互补?有哪角是互余?说明你的理由。互补:小结:互余:互余:互补:∠AOD与 ∠BOD∠1与 ∠3∠1与 ∠2∠COD与 ∠BOD∠AOC与 ∠BOC 强调互余、互补定义练习
一、填空
1、70°39′的余角是 ,补角是 。
2、如果一个角的补角是150 ° ;那么这个角的余角是 。
3、x °(x<90)的余角是 ,它的补角是 。109 °21 ′19 °21 ′(90-x) ° (180-x) °总结:锐角∠?的余角是(90 °—∠ ? )
∠?的补角是(180 °—∠ ? )60 °㈤:动手画一画:比谁快一:已知∠α,如图利用三角尺画出下列各角
① ∠α 的余角 ② ∠α 的补角⑵比较∠1与∠2的大小。(互余和互补的性质) :⑴ ∠α的余角可以怎么画?是否还有其它画法?123问:4⑷对∠α的补角是否有同样结论。⑶由⑴、⑵ 可得出何种结论。小结得出( ∠1= ∠2 )①同角或等角的余角相等②同角或等角的补角相等∠1和∠2互余,∠3和∠4互余,如果∠1=∠3,那么, ∠2和∠4相等吗?为什么?4试一试补角性质:
同角或等角的补角相等。
余角性质:
同角或等角的余角相等。㈥:范例讲解例1:如图、已知∠AOC= ∠BOD=Rt ∠。指出图中还有哪些角相等, 并说明理由。理由:解:∠COD +∠BOC=Rt ∠∴ ∠AOB +∠BOC=Rt ∠即∠AOB与 ∠COD都是∠BOC的余角∠AOB=∠COD (同角的余角相等)∠AOB= ∠COD∵ ∠AOC= ∠BOD=Rt ∠㈦:试一试:看谁会 如图A、B、O在同一直线上, ∠1= ∠2、找出图中①相等的角②互补的角。∠1与∠BOC互补的角有:解: ∠2与∠AOD∠1与∠AOD∠2与∠ BOC 相等的角有: ∠AOD= ∠BOC已知一个的补角是这个角的余角的4倍,求这个角的度数。提问:范例2:1:一个角的余角、补角怎样表示?3:能否根据题意列出等量关系。解得: x = 60°180-x = 4(90-x)2:若设这个角为x度,则其余角是_________度,补角是__________度。(90 – x)(180 – x)已知一个的补角是这个角的余角的4倍,求这个角的度数。范例2:解:设这个为x,则这个角的余角是(90-x)度,补角是(180-x)度。解得:x = 60(度)由题意得:180-x = 4(90-x)即:这个角的度数为60o㈧:做一做,看谁快3 :已知一个角的补角是它的2.5倍。求这个角的余角。2 :若∠1的补角是∠1的3倍。求∠1的度数。1:已知∠α的余角是∠α的2倍。求 ∠α的度数。 ( 解得:∠α = 30o )( 解得:这个角的余角60o)( 解得:∠1 = 45o )四:课堂小结1:互余、互补的概念及性质。2:能运用互余、互补的性质进行解题。小结∠1+ ∠2 = 90 °∠1+ ∠2 = 180 °同角或等角的余角相等。同角或等角的补角相等。ABCDEFG如图,E、F是直线DG上两点
∠BEF = ∠BFE
∠AED = ∠CFG = 90 °找出图中相等的角并说明理由。讨论∠1=120 °, ∠1与∠2互补, ∠3与∠2互余,则∠3= .
2.O为直线AB上的一点,OD平分∠AOB,
∠COE = 90 °
则∠BOC = ,
∠COD = 。检测∠DOE∠AOE30 °3.如图1-43,写出下列各图中∠AOC的余角和补角.左图中∠AOE=90°,右图中OA,OF都是直角∠BOC和直角∠BOD的角平分线. 5. 如图1-40,已知:长方形ABDC中,∠CDB是直角,∠CDA=26°,DE是∠ADB的平分线,则∠EDB=______. 6.如图1-41,已知∠DCB是直角,AC平分∠DCB,则∠ACB=______,∠DCE+∠FCB=______.
如果两个角的和是一个直角,那么这两个角叫做互为余角,其中一个角是另一个角的余角。
互为补角
如果两个角的和是一个平角,那么这两个角叫做互为补角。其中一个角是另一个角的补角。
互为余角
如果 的和是一个 ,那么这两个角叫做 余角,其中一个角是 的余角。
互为补角
如果 的和是一个 ,那么这两个角叫做 补角,其中一个角是 的补角。
两个角直角互为另一个角两个角互为另一个角平角小结:∠1 +∠2=90o①互余、互补是指两个角 若两个角的和是平角,则就说这两个角互为补角,其中一个角是另一个角的补角定 义互为余角 (互余) 若两个锐角和是一个直角,则就说这两个角互为余角,其中一个角是另一个角的余角 ②互余、互补只跟角度的大小有关与位置无关互为补角 (互补)∠α+∠β=180o数量关系注意点概 念若∠1 + ∠2 =180 °,
则 .( )
若∠1和∠2互补,
则 .( )
若∠3 + ∠4 =90 °,则 .( )
若∠3和∠4互余,
则 .( )312∠1和∠2互补互补定义∠1 + ∠2 =180 °互补定义∠3和∠4互余互余定义∠3 + ∠4 =90 °互余定义㈢:快速练一练 1:如图,已知∠1=42o, ∠2=138o, ∠3=48o,问图中有没有互余或互补的角?若有,请把它们写出来,并说明理由。 2: 如图, 点O为直线AB上一点, ∠AOB=Rt ∠, OD是∠BOC内的一条射线。图中有哪角是互补?有哪角是互余?说明你的理由。互补:小结:互余:互余:互补:∠AOD与 ∠BOD∠1与 ∠3∠1与 ∠2∠COD与 ∠BOD∠AOC与 ∠BOC 强调互余、互补定义练习
一、填空
1、70°39′的余角是 ,补角是 。
2、如果一个角的补角是150 ° ;那么这个角的余角是 。
3、x °(x<90)的余角是 ,它的补角是 。109 °21 ′19 °21 ′(90-x) ° (180-x) °总结:锐角∠?的余角是(90 °—∠ ? )
∠?的补角是(180 °—∠ ? )60 °㈤:动手画一画:比谁快一:已知∠α,如图利用三角尺画出下列各角
① ∠α 的余角 ② ∠α 的补角⑵比较∠1与∠2的大小。(互余和互补的性质) :⑴ ∠α的余角可以怎么画?是否还有其它画法?123问:4⑷对∠α的补角是否有同样结论。⑶由⑴、⑵ 可得出何种结论。小结得出( ∠1= ∠2 )①同角或等角的余角相等②同角或等角的补角相等∠1和∠2互余,∠3和∠4互余,如果∠1=∠3,那么, ∠2和∠4相等吗?为什么?4试一试补角性质:
同角或等角的补角相等。
余角性质:
同角或等角的余角相等。㈥:范例讲解例1:如图、已知∠AOC= ∠BOD=Rt ∠。指出图中还有哪些角相等, 并说明理由。理由:解:∠COD +∠BOC=Rt ∠∴ ∠AOB +∠BOC=Rt ∠即∠AOB与 ∠COD都是∠BOC的余角∠AOB=∠COD (同角的余角相等)∠AOB= ∠COD∵ ∠AOC= ∠BOD=Rt ∠㈦:试一试:看谁会 如图A、B、O在同一直线上, ∠1= ∠2、找出图中①相等的角②互补的角。∠1与∠BOC互补的角有:解: ∠2与∠AOD∠1与∠AOD∠2与∠ BOC 相等的角有: ∠AOD= ∠BOC已知一个的补角是这个角的余角的4倍,求这个角的度数。提问:范例2:1:一个角的余角、补角怎样表示?3:能否根据题意列出等量关系。解得: x = 60°180-x = 4(90-x)2:若设这个角为x度,则其余角是_________度,补角是__________度。(90 – x)(180 – x)已知一个的补角是这个角的余角的4倍,求这个角的度数。范例2:解:设这个为x,则这个角的余角是(90-x)度,补角是(180-x)度。解得:x = 60(度)由题意得:180-x = 4(90-x)即:这个角的度数为60o㈧:做一做,看谁快3 :已知一个角的补角是它的2.5倍。求这个角的余角。2 :若∠1的补角是∠1的3倍。求∠1的度数。1:已知∠α的余角是∠α的2倍。求 ∠α的度数。 ( 解得:∠α = 30o )( 解得:这个角的余角60o)( 解得:∠1 = 45o )四:课堂小结1:互余、互补的概念及性质。2:能运用互余、互补的性质进行解题。小结∠1+ ∠2 = 90 °∠1+ ∠2 = 180 °同角或等角的余角相等。同角或等角的补角相等。ABCDEFG如图,E、F是直线DG上两点
∠BEF = ∠BFE
∠AED = ∠CFG = 90 °找出图中相等的角并说明理由。讨论∠1=120 °, ∠1与∠2互补, ∠3与∠2互余,则∠3= .
2.O为直线AB上的一点,OD平分∠AOB,
∠COE = 90 °
则∠BOC = ,
∠COD = 。检测∠DOE∠AOE30 °3.如图1-43,写出下列各图中∠AOC的余角和补角.左图中∠AOE=90°,右图中OA,OF都是直角∠BOC和直角∠BOD的角平分线. 5. 如图1-40,已知:长方形ABDC中,∠CDB是直角,∠CDA=26°,DE是∠ADB的平分线,则∠EDB=______. 6.如图1-41,已知∠DCB是直角,AC平分∠DCB,则∠ACB=______,∠DCE+∠FCB=______.
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
