7、6余角和补角[上学期]

课件18张PPT。余角和补角一、复习回顾1、1周角=______度
2、1平角=______度
3、1直角=______度
4、平角是一条直线吗？
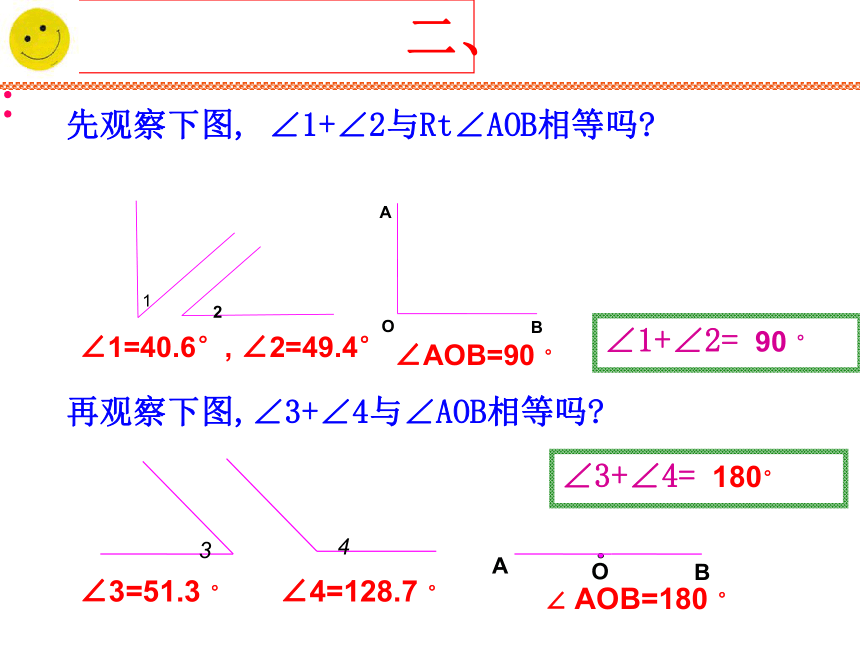
5、周角是一条射线吗？36018090（ ）（ ）∠AOB=90 ° ∠1=40.6°, ∠2=49.4°∠ AOB=180 °∠4=128.7 °∠3=51.3 ° 二、 合作学习:先观察下图, ∠1+∠2与Rt∠AOB相等吗?再观察下图,∠3+∠4与∠AOB相等吗?∠1+∠2= 90 °∠3+∠4= 180°余角 与 补角 的定义余角:如果两个角的和是直角,那么称这两个角互为余角.
简称互余.
补角:如果两个角的和是平角,那么称这两个角互为补角.
简称互补.
补角与余角是两个角之间的相互关系。
补角与余角与角的位置无关，只与它的度数有关。互为余角的有： ∠1和∠ 3.1、 如图，已知∠1=42°，
∠ 2=138°， ∠ 3=48°，
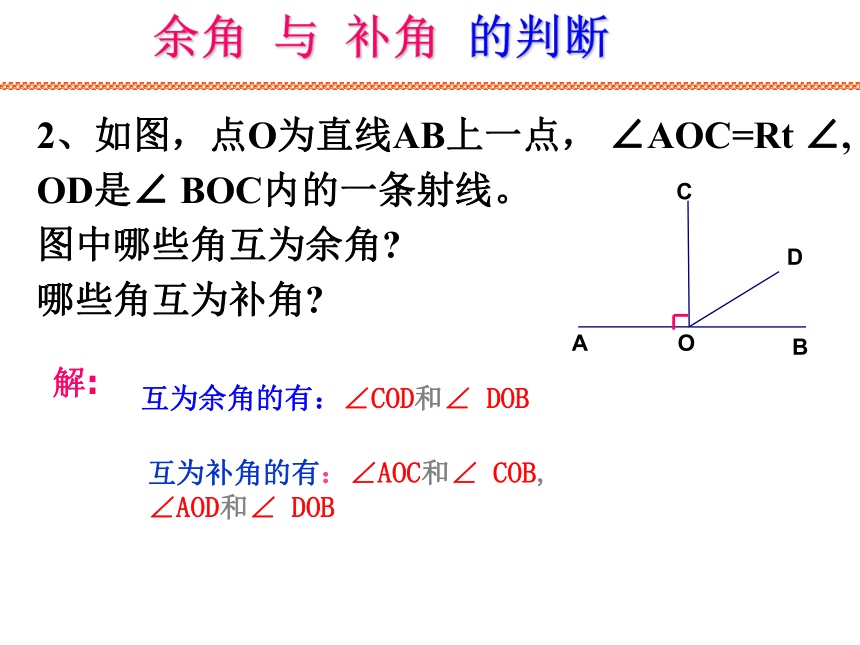
问图中有没有互余或互补的角?余角 与 补角 的判断互为补角的有：∠1和∠ 2解:2、如图，点O为直线AB上一点， ∠AOC=Rt ∠,
OD是∠ BOC内的一条射线。
图中哪些角互为余角?
哪些角互为补角?余角 与 补角 的判断互为余角的有：∠COD和∠ DOB解:互为补角的有：∠AOC和∠ COB, ∠AOD和∠ DOB解:∠BOC=∠AOB -∠AOC
=90°- ∠AOC∠AOD= ∠AOB -∠BOD
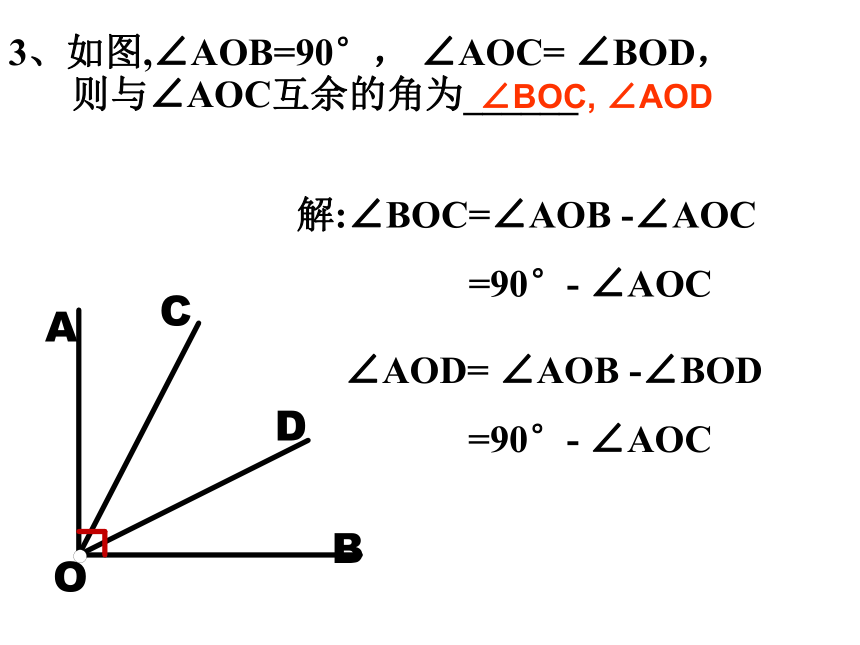
=90°- ∠AOC∠BOC, ∠AOD 4、填空：
（1） ∠α的余角=90°－ ；
（2） ∠ β的余角= －∠ β 。余角 与 补角 的 性 质∠α90°若∠α =∠ β,那么∠α的余角和∠ β的余角有何关系?例1 如图，已知∠AOC= ∠BOD=Rt ∠ ，
指出图中还有哪些角相等，并说明理由。例 题 解 析P183解:∠AOB = ∠COD∵ ∠AOC =∠BOD=Rt ∠∴ ∠AOB =∠DOC∴ ∠AOB +∠BOC=Rt ∠ ∠DOC +∠BOC=Rt ∠即∠AOB 与∠DOC 都是∠BOC的余角(理由?)(同角的余角相等)
例2 已知一个角的补角是这个角的余角的4倍，
求这个角的度数。例 题 解 析解:设这个角为x度,则这个角的余角是 度,补角是 度.(90-x)(180-x)由题意,得180-x=4(90-x)解方程,得x=60(度)答：这个角的度数为60°1、判断：
①一个角的余角一定是锐角（ ）
②一个角的补角一定是钝角（ ）
③若∠1+∠2+∠3=90°，那么∠1、∠2、∠3
互为余角（ ）√╳╳三、自主评价、反馈信息C 2、要测量两堵墙所成的∠ AOB的度数，但人不能进入围墙，如何测量？5.如图，OA⊥OB，OC⊥OD，且∠ COB=50°，则∠AOD= 。130°3.已知∠α= 60°32′则∠α的余角等于_____ 。
则∠α的补角等于 .29°28′课 内 练 习119°28′4. 如果∠α的余角是∠α的2倍,则∠α= .如果∠1的补角是∠1的3倍，则∠1= .30 °45 °6、如图，OB平分∠COD，∠AOB=90°，∠AOC=125°，求比∠COD的补角小19°3′59″的角的度数。解：∠BOC＝∠BOD ＝ ∠BOC ＝35°∠COD ＝35°×2 ＝70°∠COD的补角 ＝110°∴所求的角 ＝110°－19°3′59″＝90°56′1″。DBCOA拓 展 练 习∠AOC－∠AOB ＝125°－90°
＝35°7、如图2，点O在直线AB上，OD平分∠ AOC，
OE平分∠COB，
①那么∠ EOD= ；
②图中互余角有 对，互补角有 对。图290 °45注意完全平方公式和平方差公式不同：余角、补角的概念：余角、补角的性质：（1） 和为直角的两个角称互为余角；
（2） 和为平角的两个角称互为补角；（1） 同角或等角的余角相等；
（2） 同角或等角的补角相等；今天我们学了什么？作业1、 P184~185
2、作业本总结:1、互为余角（互余）、互为补角（互补）是两个角之间的数量关系，不是位置关系。2、互为余角的两个角不一定是直角中分成的两个角，互为补角的两个角不一定是平角中分成的两个角。再见