7.6余角和补角[上学期]
图片预览




文档简介
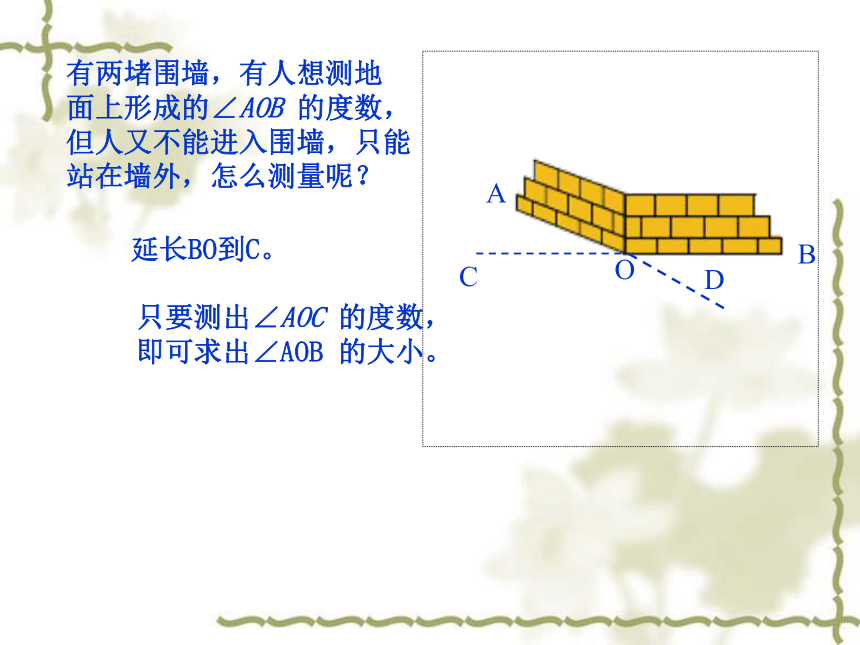
课件21张PPT。AOBC有两堵围墙,有人想测地
面上形成的∠AOB 的度数,
但人又不能进入围墙,只能
站在墙外,怎么测量呢?延长BO到C。只要测出∠AOC 的度数,
即可求出∠AOB 的大小。
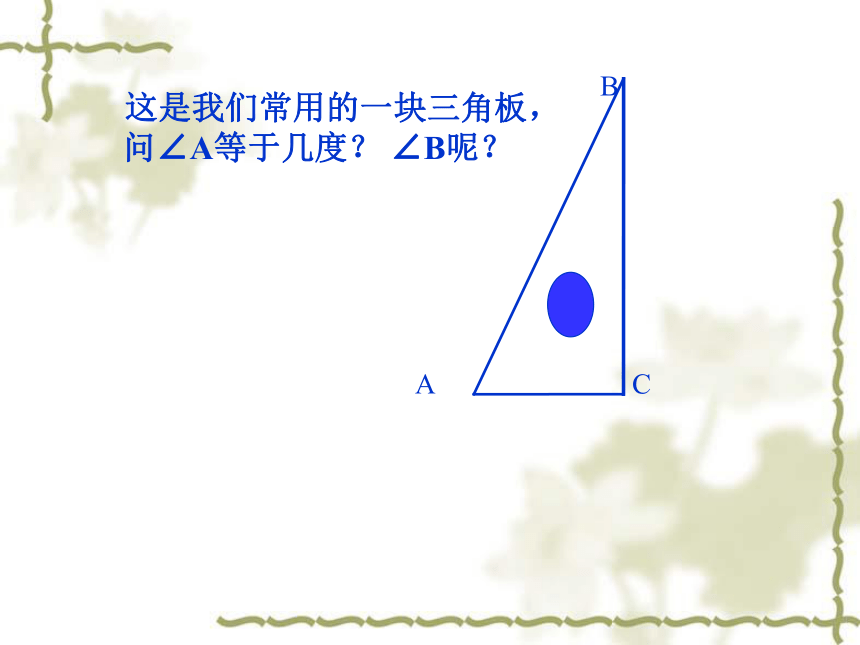
D 这是我们常用的一块三角板,
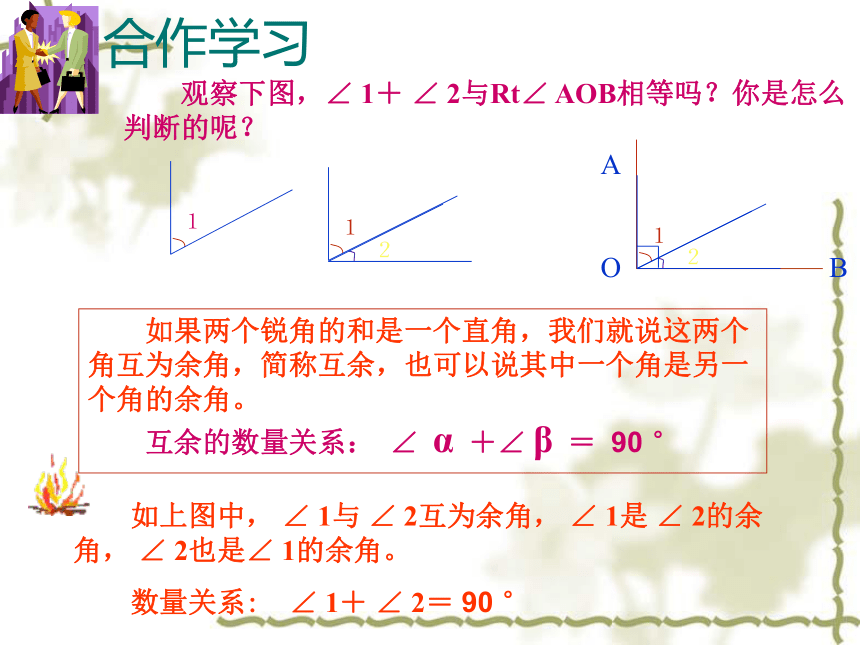
问∠A等于几度? ∠B呢?7.6余角和补角合作学习 观察下图,∠ 1+ ∠ 2与Rt∠ AOB相等吗?你是怎么判断的呢? 如果两个锐角的和是一个直角,我们就说这两个角互为余角,简称互余,也可以说其中一个角是另一个角的余角。
如上图中, ∠ 1与 ∠ 2互为余角, ∠ 1是 ∠ 2的余角, ∠ 2也是∠ 1的余角。
互余的数量关系: ∠ α +∠ β = 90 °
数量关系: ∠ 1+ ∠ 2= 90 °A
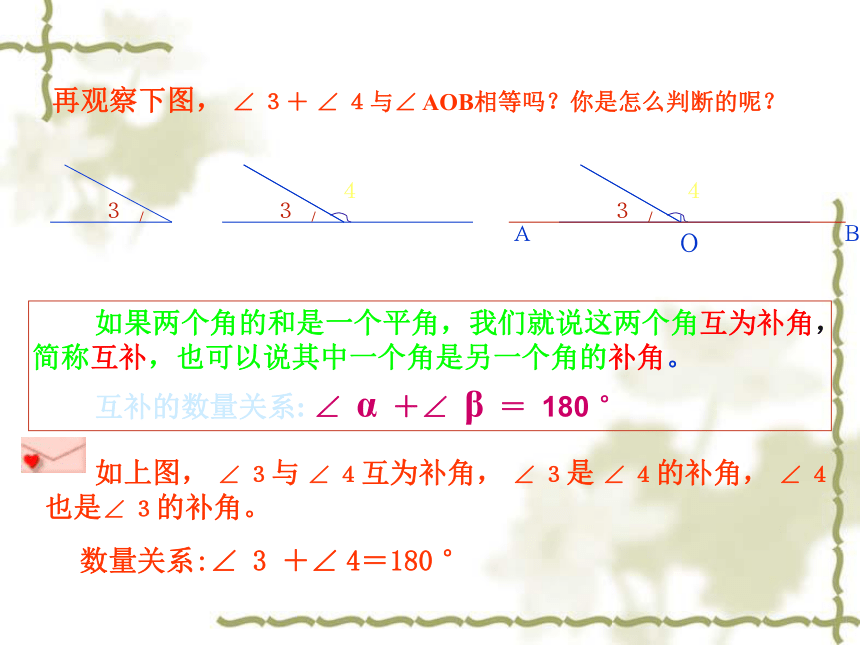
O B再观察下图, ∠ 3+ ∠ 4与∠ AOB相等吗?你是怎么判断的呢? 如果两个角的和是一个平角,我们就说这两个角互为补角,简称互补,也可以说其中一个角是另一个角的补角。
如上图, ∠ 3与 ∠ 4互为补角, ∠ 3是 ∠ 4的补角, ∠ 4也是∠ 3的补角。互补的数量关系: ∠ α +∠ β = 180 °数量关系:∠ 3 +∠ 4=180 °1、定义中的“互为”一词如何理解?2、互补、互余的两角是否一定有公共顶点或公共边?3、?1与?2互补,除用符号语言表示为?1+ ?2=180°外,还可以用其它形式等式表示为______。如果?1与?2互补,那么?1的补角是?2 ,而?2的补角是?1 ;如果?1与?2互余,那么?1的余角是?2 , ?2的余角是?1。互补或互余的两角不一定有公共顶点或公共边。还可以表示为: ?1=180°- ?2,或 ?2=180°- ?1 。议一议根据互余互补你会填吗?180°60°150°29°28′119°28′(90-x)°
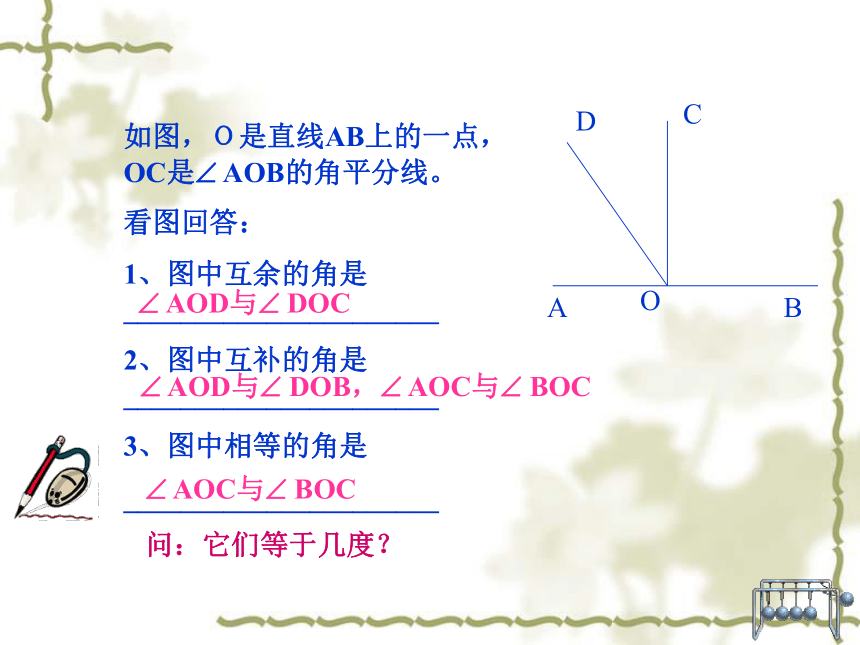
(180-x)°150°如图,O是直线AB上的一点,OC是? AOB的角平分线。
看图回答:
1、图中互余的角是______________________
2、图中互补的角是______________________
3、图中相等的角是
______________________? AOD与? DOC? AOD与? DOB,? AOC与? BOC? AOC与? BOC问:它们等于几度?变式:如右图,在上题的基础上添加一条射线OE,使得? DOE是一个直角,回答下列问题:图中? DOC的余角有
___________________图中? AOD的余角有
___________________(3) 通过上述两小题你能得到什么结论?(4) ? AOD和? COE的补角分别是________________(5) 通过此题,你又能得到什么结论?? AOD与?COE? DOC与?BOE ? BOD与?BOD同 角 的 余 角 相 等。等 角 的 补 角 相 等。(等角)(同角)(如此图中, ∵ ? AOD + ? COD =90° ,
? COE + ? COD = 90°, ∴ ? AOD= ? COE)同角或等角的余角相等。若∠α+∠β=90°,∠β+∠γ=90°,则∠α=∠γ。同角或等角的补角相等。若∠α+∠β=180°,∠β+∠γ=180°,则∠α=∠γ。余角和补角的性质1、判断题:
(1)互余的两个角必定都是锐角。 ( )
(2) ? ? =90°,那么它是余角。 ( )
(3)一个角的补角必定是钝角。 ( )
(4)两个角互补,那么这两个角中,必定一个是锐角,另一个是钝角。 ( )
????断真伪
2、 图中A、O、D三点在同一直线上, ? AOB= ? COD,哪几对角互为补角? ? AOB与?BOD、? AOB与?AOC、
? COD与?COA、?COD与?BOD
谁最棒你找对了吗?1、如图1,∠AOB=∠COD=Rt∠,请找出另外相等的角,并说明理由。2、图2中的∠1、∠2、∠3、∠4,哪些是相等的角,为什么?典型例题已知一个角的补角是这个角的余角的4倍,求这个角的度数。做一做一个角的补角减去20°后,等于这个角的余角的2倍,求这个角的度数。探索思考题:一只闹钟,两点整的时候,时针与分针所
夹的角∠α是 度,它的余角是 度。若时针与分针所夹的角恰好是∠α的补角,
此时刚好是整点,问应是几点整?6030课内练习P184. 1,2,3。 判断下列说法是否正确,并说明理由。
(1)一个锐角的补角一定是钝角。
(2)如果两个角互补,那么 这两个角中,一个是锐角,另一个是钝角。
(3)如果一个角的余角和补角都存在,那么这个角的余角一定比这个角的补角小。下图中,OA是表示南偏西30o方向上的一条射线,仿照这条射线,画出表示下列方向的射线:(1)北偏西20o;(2)南偏东60o; (3)西南方向(即南偏西45o)。30o20o60o45o表示(1)、(2)方向的两条射线所成的角是多少度?表示(2)、(3)方向的两条射线所成的角呢?在日常生活中,我们什么时候会用到这样的表示法?140o105o表示目标方位思考在一幅学校的地图上,有教学楼、食堂、图书馆三地,但被墨迹污染,图书馆的具体位置看不清,只知道图书馆在教学楼的东北方向,在食堂的南偏西60o方向,你能确定图书馆的位置吗?图书馆45o60oCDENAOBM?1+ ?2=90°?1+ ?2=180°同角(等角)的余角相等。同角(等角)的补角相等。课堂小结谢谢大家!下课作业:书P184-185作业题
大作业本P38 7.6节
面上形成的∠AOB 的度数,
但人又不能进入围墙,只能
站在墙外,怎么测量呢?延长BO到C。只要测出∠AOC 的度数,
即可求出∠AOB 的大小。
D 这是我们常用的一块三角板,
问∠A等于几度? ∠B呢?7.6余角和补角合作学习 观察下图,∠ 1+ ∠ 2与Rt∠ AOB相等吗?你是怎么判断的呢? 如果两个锐角的和是一个直角,我们就说这两个角互为余角,简称互余,也可以说其中一个角是另一个角的余角。
如上图中, ∠ 1与 ∠ 2互为余角, ∠ 1是 ∠ 2的余角, ∠ 2也是∠ 1的余角。
互余的数量关系: ∠ α +∠ β = 90 °
数量关系: ∠ 1+ ∠ 2= 90 °A
O B再观察下图, ∠ 3+ ∠ 4与∠ AOB相等吗?你是怎么判断的呢? 如果两个角的和是一个平角,我们就说这两个角互为补角,简称互补,也可以说其中一个角是另一个角的补角。
如上图, ∠ 3与 ∠ 4互为补角, ∠ 3是 ∠ 4的补角, ∠ 4也是∠ 3的补角。互补的数量关系: ∠ α +∠ β = 180 °数量关系:∠ 3 +∠ 4=180 °1、定义中的“互为”一词如何理解?2、互补、互余的两角是否一定有公共顶点或公共边?3、?1与?2互补,除用符号语言表示为?1+ ?2=180°外,还可以用其它形式等式表示为______。如果?1与?2互补,那么?1的补角是?2 ,而?2的补角是?1 ;如果?1与?2互余,那么?1的余角是?2 , ?2的余角是?1。互补或互余的两角不一定有公共顶点或公共边。还可以表示为: ?1=180°- ?2,或 ?2=180°- ?1 。议一议根据互余互补你会填吗?180°60°150°29°28′119°28′(90-x)°
(180-x)°150°如图,O是直线AB上的一点,OC是? AOB的角平分线。
看图回答:
1、图中互余的角是______________________
2、图中互补的角是______________________
3、图中相等的角是
______________________? AOD与? DOC? AOD与? DOB,? AOC与? BOC? AOC与? BOC问:它们等于几度?变式:如右图,在上题的基础上添加一条射线OE,使得? DOE是一个直角,回答下列问题:图中? DOC的余角有
___________________图中? AOD的余角有
___________________(3) 通过上述两小题你能得到什么结论?(4) ? AOD和? COE的补角分别是________________(5) 通过此题,你又能得到什么结论?? AOD与?COE? DOC与?BOE ? BOD与?BOD同 角 的 余 角 相 等。等 角 的 补 角 相 等。(等角)(同角)(如此图中, ∵ ? AOD + ? COD =90° ,
? COE + ? COD = 90°, ∴ ? AOD= ? COE)同角或等角的余角相等。若∠α+∠β=90°,∠β+∠γ=90°,则∠α=∠γ。同角或等角的补角相等。若∠α+∠β=180°,∠β+∠γ=180°,则∠α=∠γ。余角和补角的性质1、判断题:
(1)互余的两个角必定都是锐角。 ( )
(2) ? ? =90°,那么它是余角。 ( )
(3)一个角的补角必定是钝角。 ( )
(4)两个角互补,那么这两个角中,必定一个是锐角,另一个是钝角。 ( )
????断真伪
2、 图中A、O、D三点在同一直线上, ? AOB= ? COD,哪几对角互为补角? ? AOB与?BOD、? AOB与?AOC、
? COD与?COA、?COD与?BOD
谁最棒你找对了吗?1、如图1,∠AOB=∠COD=Rt∠,请找出另外相等的角,并说明理由。2、图2中的∠1、∠2、∠3、∠4,哪些是相等的角,为什么?典型例题已知一个角的补角是这个角的余角的4倍,求这个角的度数。做一做一个角的补角减去20°后,等于这个角的余角的2倍,求这个角的度数。探索思考题:一只闹钟,两点整的时候,时针与分针所
夹的角∠α是 度,它的余角是 度。若时针与分针所夹的角恰好是∠α的补角,
此时刚好是整点,问应是几点整?6030课内练习P184. 1,2,3。 判断下列说法是否正确,并说明理由。
(1)一个锐角的补角一定是钝角。
(2)如果两个角互补,那么 这两个角中,一个是锐角,另一个是钝角。
(3)如果一个角的余角和补角都存在,那么这个角的余角一定比这个角的补角小。下图中,OA是表示南偏西30o方向上的一条射线,仿照这条射线,画出表示下列方向的射线:(1)北偏西20o;(2)南偏东60o; (3)西南方向(即南偏西45o)。30o20o60o45o表示(1)、(2)方向的两条射线所成的角是多少度?表示(2)、(3)方向的两条射线所成的角呢?在日常生活中,我们什么时候会用到这样的表示法?140o105o表示目标方位思考在一幅学校的地图上,有教学楼、食堂、图书馆三地,但被墨迹污染,图书馆的具体位置看不清,只知道图书馆在教学楼的东北方向,在食堂的南偏西60o方向,你能确定图书馆的位置吗?图书馆45o60oCDENAOBM?1+ ?2=90°?1+ ?2=180°同角(等角)的余角相等。同角(等角)的补角相等。课堂小结谢谢大家!下课作业:书P184-185作业题
大作业本P38 7.6节
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
