浙教版数学九年级下册1.2《锐角三角函数的计算》 课件(共17张PPT)
文档属性
| 名称 | 浙教版数学九年级下册1.2《锐角三角函数的计算》 课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-15 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
锐角三角函数的计算
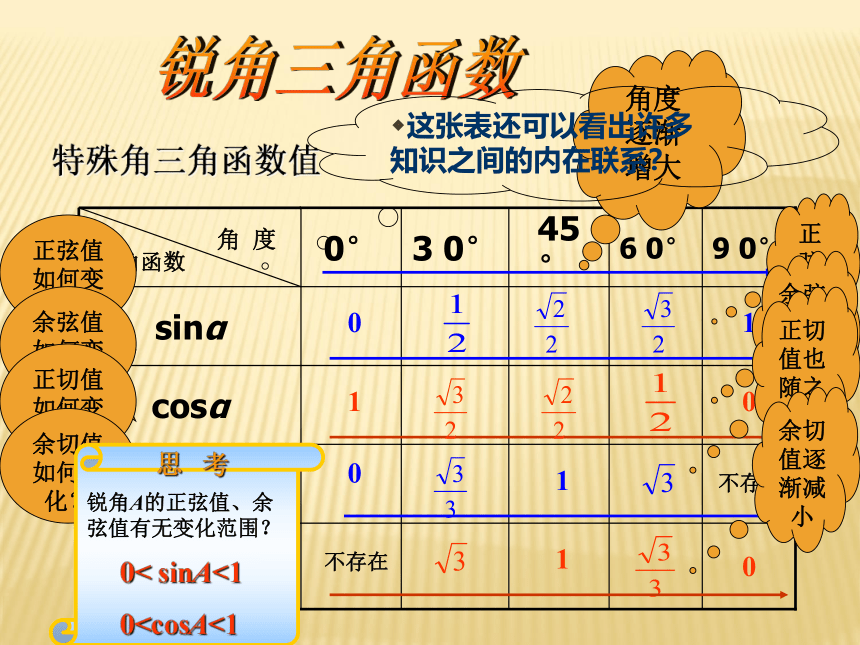
cotα
tanα
cosα
sinα
9 0°
6 0°
45 °
3 0°
0°
角 度
三角函数
特殊角三角函数值
1
0
0
1
1
1
0
0
不存在
不存在
角度
逐渐
增大
正弦值如何变化?
正弦值也增大
余弦值如何变化?
余弦值逐渐减小
正切值如何变化?
正切值也随之增大
余切值如何变化?
余切值逐渐减小
思 考
锐角A的正弦值、余弦值有无变化范围?
0< sinA<1
0这张表还可以看出许多知识之间的内在联系?
二.新课引入
同学们,前面我们学习了特殊角30°45°60°的三角函数值,一些非特殊角(如17°56°89°等)的三角函数值又怎么求呢?
这一节课我们就学习借助计算器来完成这个任务.
1、在Rt△ACB中, ∠C=90°,∠A=30 °,若BC=a,则AB=______,AC= _______,∠B=______.
2、在Rt△ACB中,∠C=90°,若∠A =40°,BC=m,则∠B= ________,AC= ________,AB=_______.
2a
60°
?
a
?
50°
一般锐角的三角函数值该怎么算呢?
这节课我们介绍如何利用计算器求已知锐角的三角函数值和由三角函数值求对应的锐角.
在直角三角形中,若一个锐角确定,那么这个角的对边,邻边和斜边之间的比值也随之确定.
直角三角形中边与角的关系:锐角三角函数.
b
A
B
C
a
┌
c
tanA=
a
b
tanB=
b
a
锐角A的正弦、余弦、和正切统称∠A的三角函数
脑中有“图”,心中有“式”
例1 如图1-11,在Rt△ABC中,∠C=90°,AB=12cm,∠A=35°.求△ABC的周长和面积(周长精确到0.1cm,面积精确到0.1cm2).
解 在Rt△ABC中,
答:△ABC的周长约为28.7cm,面积约为33.8cm2.
△ABC的面积=
∴△ABC的周长
=AB+BC+AC
=AB+AB·sinA+AB·cosA
=AB(1+sinA+cosA)
=12(1+sin35°+cos35°)≈28.7(cm);
例2 根据下面的条件,求锐角β的大小(精确到1").
(1)sinβ=0.4511.(2)cosβ=0.7875. (3)tanβ=1.4036.
解(1)按键顺序为:
得β≈26°48′51″.
(2)按键顺序为:
得β≈38°12′52″.
(3)按键顺序为:
得β≈54°31′55″.
于是有sin∠BOC=
如图1-12,作OC⊥AB,垂足为C,则OC平分∠AOB.
在Rt△OCB中,
分析 因为 的半径已知,根据弧长公式
要求弯道 的长,只要求出 所对圆心角∠AOB的度数.
例3 如图1-12,一段公路弯道呈圆弧形,测得弯道 两端的距离为200m, 的半径为1000m.求弯道的长(精确到0.1m).
∴∠AOC=5044’21.01”
∴∠AOB≈11.480
∴AB=
11.48×1000π
⌒
180
≈200.3(m).
答:弯道长约为200.3m.
三、应用举例
1.求已知锐角的三角函数值:
1、求sin63°52′41″的值(精确到0.0001)
解 先用如下方法将角度单位状态设定为“度”:
再按下列顺序依次按键:
显示结果为0.897 859 012.
所以 sin63゜52′41″≈0.8979
SHIFT
MODE
(SETUP)
3
D
显示
1.用计算器求sin 40°,cos40°,tan40°的值.(精确到0.0001)
2.用计算器求下列三角函数值:(精确到0.0001)
(1) sin 72°,cos36°,tan55°;
(2) sin 7°2′25″,cos29°13′44″,tan88°21′.
(2)由锐角三角函数值求锐角:
已知tan x=0.7410,求锐角x.(精确到1′)
解 在角度单位状态为“度”的情况下(屏幕显示出
),按下列顺序
依次按键:
显示结果为36.538 445 77.
再按键:
显示结果为36゜32′18.4.
所以,x≈36゜32′.
已知cos x=0.1950,求锐角x.(精确到1′)
分析 根据tan x=
可以求出tan x的值,然后根据例4的方法就可
以求出锐角x的值.
x=78°57′57″
2.已知锐角a的三角函数值,使用计算器求锐角x (精确到1′)
(1)sin a=0.2476; (2)cos a=0.4174;
(3)tan a=0.1890;
答案: (1)α≈14°20′;
(3)α≈10°42′.
(2)α≈65°20′;
练习:
3.用计算器求下式的值.(精确到0.0001)
sin81°32′17″+cos38°43′47″
答案:1.7692
用计算器计算:sin36°与cos54°,它们有什么关系?sin24°与cos56°呢?你从中得出什么规律吗?
你能够证明上面的结论吗?
同学们说出:怎样运用自己的计算器求出已知锐角的三角函数值和由三角函数值求对应的锐角?
锐角三角函数的计算
cotα
tanα
cosα
sinα
9 0°
6 0°
45 °
3 0°
0°
角 度
三角函数
特殊角三角函数值
1
0
0
1
1
1
0
0
不存在
不存在
角度
逐渐
增大
正弦值如何变化?
正弦值也增大
余弦值如何变化?
余弦值逐渐减小
正切值如何变化?
正切值也随之增大
余切值如何变化?
余切值逐渐减小
思 考
锐角A的正弦值、余弦值有无变化范围?
0< sinA<1
0
二.新课引入
同学们,前面我们学习了特殊角30°45°60°的三角函数值,一些非特殊角(如17°56°89°等)的三角函数值又怎么求呢?
这一节课我们就学习借助计算器来完成这个任务.
1、在Rt△ACB中, ∠C=90°,∠A=30 °,若BC=a,则AB=______,AC= _______,∠B=______.
2、在Rt△ACB中,∠C=90°,若∠A =40°,BC=m,则∠B= ________,AC= ________,AB=_______.
2a
60°
?
a
?
50°
一般锐角的三角函数值该怎么算呢?
这节课我们介绍如何利用计算器求已知锐角的三角函数值和由三角函数值求对应的锐角.
在直角三角形中,若一个锐角确定,那么这个角的对边,邻边和斜边之间的比值也随之确定.
直角三角形中边与角的关系:锐角三角函数.
b
A
B
C
a
┌
c
tanA=
a
b
tanB=
b
a
锐角A的正弦、余弦、和正切统称∠A的三角函数
脑中有“图”,心中有“式”
例1 如图1-11,在Rt△ABC中,∠C=90°,AB=12cm,∠A=35°.求△ABC的周长和面积(周长精确到0.1cm,面积精确到0.1cm2).
解 在Rt△ABC中,
答:△ABC的周长约为28.7cm,面积约为33.8cm2.
△ABC的面积=
∴△ABC的周长
=AB+BC+AC
=AB+AB·sinA+AB·cosA
=AB(1+sinA+cosA)
=12(1+sin35°+cos35°)≈28.7(cm);
例2 根据下面的条件,求锐角β的大小(精确到1").
(1)sinβ=0.4511.(2)cosβ=0.7875. (3)tanβ=1.4036.
解(1)按键顺序为:
得β≈26°48′51″.
(2)按键顺序为:
得β≈38°12′52″.
(3)按键顺序为:
得β≈54°31′55″.
于是有sin∠BOC=
如图1-12,作OC⊥AB,垂足为C,则OC平分∠AOB.
在Rt△OCB中,
分析 因为 的半径已知,根据弧长公式
要求弯道 的长,只要求出 所对圆心角∠AOB的度数.
例3 如图1-12,一段公路弯道呈圆弧形,测得弯道 两端的距离为200m, 的半径为1000m.求弯道的长(精确到0.1m).
∴∠AOC=5044’21.01”
∴∠AOB≈11.480
∴AB=
11.48×1000π
⌒
180
≈200.3(m).
答:弯道长约为200.3m.
三、应用举例
1.求已知锐角的三角函数值:
1、求sin63°52′41″的值(精确到0.0001)
解 先用如下方法将角度单位状态设定为“度”:
再按下列顺序依次按键:
显示结果为0.897 859 012.
所以 sin63゜52′41″≈0.8979
SHIFT
MODE
(SETUP)
3
D
显示
1.用计算器求sin 40°,cos40°,tan40°的值.(精确到0.0001)
2.用计算器求下列三角函数值:(精确到0.0001)
(1) sin 72°,cos36°,tan55°;
(2) sin 7°2′25″,cos29°13′44″,tan88°21′.
(2)由锐角三角函数值求锐角:
已知tan x=0.7410,求锐角x.(精确到1′)
解 在角度单位状态为“度”的情况下(屏幕显示出
),按下列顺序
依次按键:
显示结果为36.538 445 77.
再按键:
显示结果为36゜32′18.4.
所以,x≈36゜32′.
已知cos x=0.1950,求锐角x.(精确到1′)
分析 根据tan x=
可以求出tan x的值,然后根据例4的方法就可
以求出锐角x的值.
x=78°57′57″
2.已知锐角a的三角函数值,使用计算器求锐角x (精确到1′)
(1)sin a=0.2476; (2)cos a=0.4174;
(3)tan a=0.1890;
答案: (1)α≈14°20′;
(3)α≈10°42′.
(2)α≈65°20′;
练习:
3.用计算器求下式的值.(精确到0.0001)
sin81°32′17″+cos38°43′47″
答案:1.7692
用计算器计算:sin36°与cos54°,它们有什么关系?sin24°与cos56°呢?你从中得出什么规律吗?
你能够证明上面的结论吗?
同学们说出:怎样运用自己的计算器求出已知锐角的三角函数值和由三角函数值求对应的锐角?
