1.1认识三角形（1）[下学期]

课件19张PPT。1.1 认识三角形(1)生活中的三角形！ 在我们的生活中几乎随处可见三角形。它简单，有趣，也十分有用。三角形可以帮助我们更好认识周围世界，解决很多的实际问题。因此，我们要更深一步的认识三角形。你了解三角形的哪些知识 呢？
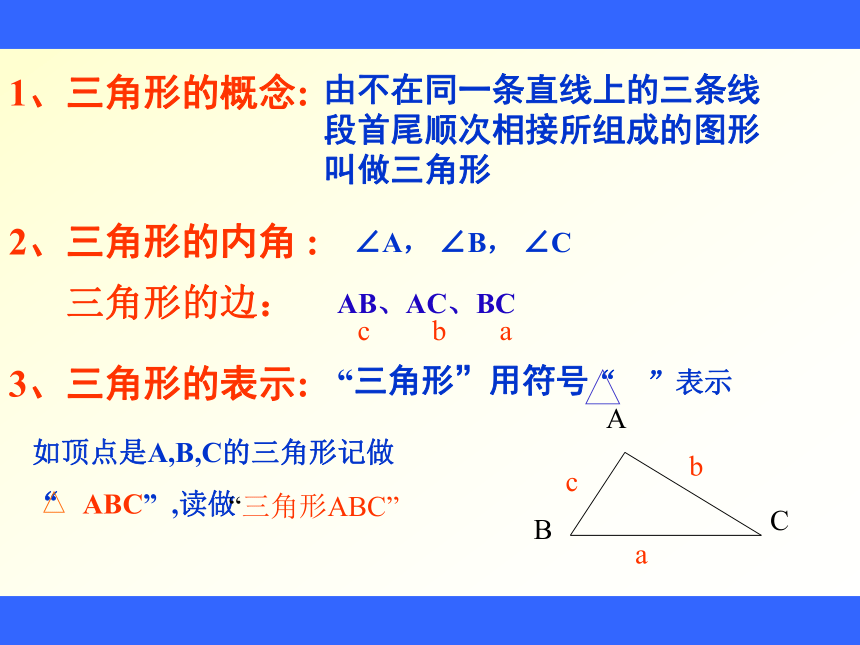
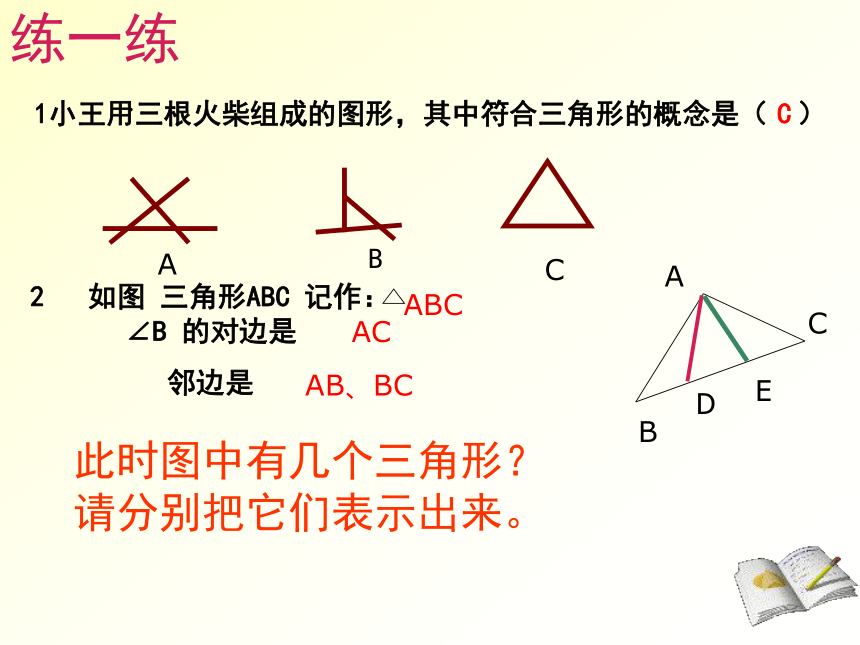
1、三角形的概念:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形3、三角形的表示: 2、三角形的内角 : ∠A， ∠B， ∠Cabc三角形的边：AB、AC、BC cba此时图中有几个三角形？请分别把它们表示出来。1小王用三根火柴组成的图形，其中符合三角形的概念是（ ）练一练ACAB、BC2 如图 三角形ABC 记作： ∠B 的对边是
邻边是
C 练一练1 如图，请写出：
(1)图中各三角形；
(2)每一个三角形的三条边和三个内角。解（1）（2）试一试： (1)任意画一个三角形，量出它的三边长度，并填空：
a=______;b=_______;c=______(2)计算并比较：
a+b____c; b+c____a; c+a____b
(3)通过以上的计算你认为三角形的三边存在怎样的关系？任何两边的和大于第三边你知道为什么吗？
三角形边的性质: 三角形任何两边的和大于第三边
a+b>c
a+c>b
b+c>a比较：a-b____c; b-c____a; c-a____b
三角形任何两边的差小于第三边。 ∴a+b>c , 线段a,b,c能组成三角形。 解： (1) ∵最长的线段 c= 5 cma+b=2.5+3= 5.5 cm解后反思：判断三条线段能否组成一个三角形的简便方法是：
（1）用较小两边的和与最大边的大小比较
（三角形任何两边的和大于第三边）（2）用最大边与最小边的差与第三边的大小比较
（三角形任何两边的差小于第三边）
由下列长度的三条线段能组成三角形吗?
请说明理由.
(1)1cm,2cm,3.5cm
(2)4cm,5cm,9cm
(3)6cm,8cm,13cm练一练2 有两根长度分别为5㎝和8㎝的木棒，
⑴用长度为2㎝的木棒与它们能摆成三角形吗？为什么？⑶在能摆成三角形时， 第三边能用的木棒
长度范围是什么？尝试乐园希望你能尝试到成功的快乐⑵长度为13㎝的木棒呢？你能说出几种能摆成三 角形的木棒长度吗？两边之差<第三边<两边之和a-b　　我们能不能运用今天所学的知识解释这一现象？十字路口(1)2AD CD
(2)AB AC+BC
(3)BD BC
(4)如果D是AB的中点,AD=5,AC=8,则BC的取值范围是
.
(5)如果AB=2CD,D为AB的中点,则AB AC
AC+AD CD><<2 < BC < 18>>58解: ∵两边之差 < 第三边 < 两边之和
∴7-3 < 第三边 < 7+3
即 4 < 第三边 < 10∴第三边长是6或8备选题 2.如图,共有 个三角形,请分别将它们
用符号表示出来:
.83.下列各组线段能构成三角形三边的是( )
A. 2cm,2cm,4cm B. 4cm,5cm,9cm
C. 3cm,4cm,5cm D. 7cm,4cm,12cmC4. 如图,D是 的边BC的中点,BC=8,
AD=5,则AB的取值范围为 .1 < AB < 9 5.已知 a , b , c 是三角形的三边,则(a-b+c).(a-b-c)的符号
为 , 理由是 .负号两边之和大于第三边6.已知A ， B两点,若要取一点C,使线段AC+BC 最小,
那么C的位置应在什么地方?为什么?C在线段AB上课堂小结三角形的概念
三角形的基本要素
三角形的表示方法
三角形三边之间的关系
学习了本节课
你有哪些收获？ 作业