1.1认识三角形(1)[下学期]

课件15张PPT。
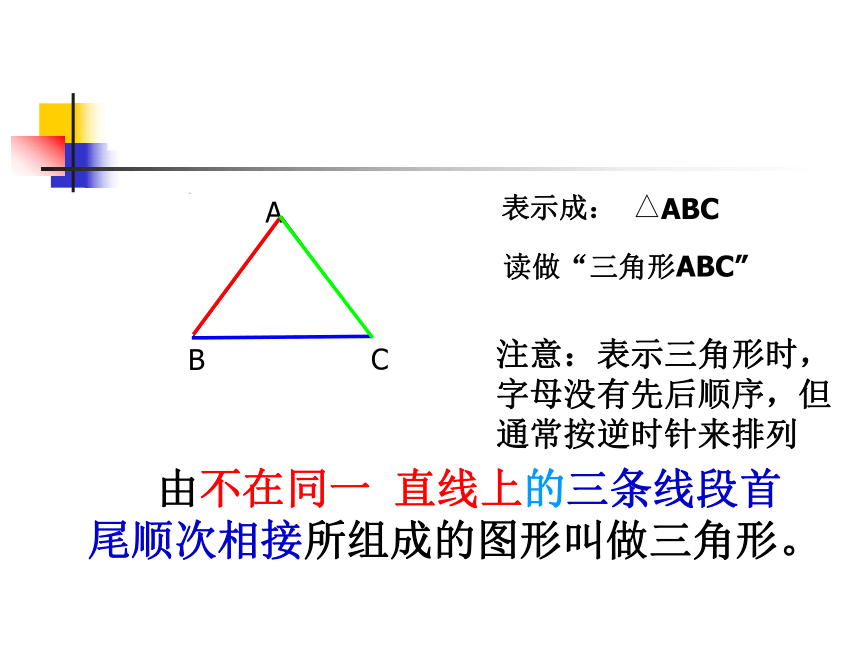
1.1认识三角形认识三角形·埃及金字塔你能举出在生活中看到的三角形的例子吗？你熟悉下面的图形吗?它由哪些基本的图形组成？注意：表示三角形时，
字母没有先后顺序，但通常按逆时针来排列 由不在同一 直线上的三条线段首尾顺次相接所组成的图形叫做三角形。ABC读做“三角形ABC”
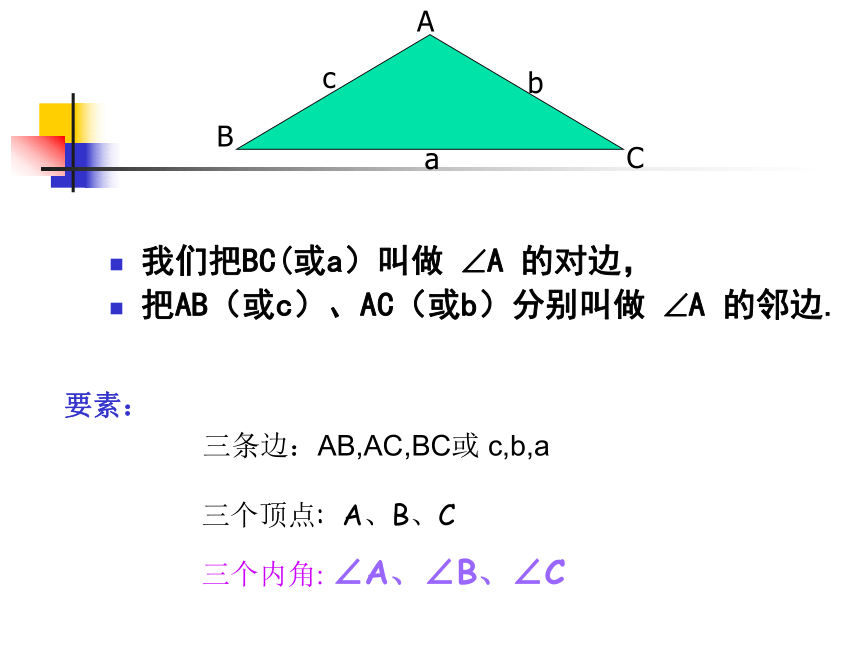
我们把BC(或a）叫做 ?A 的对边，
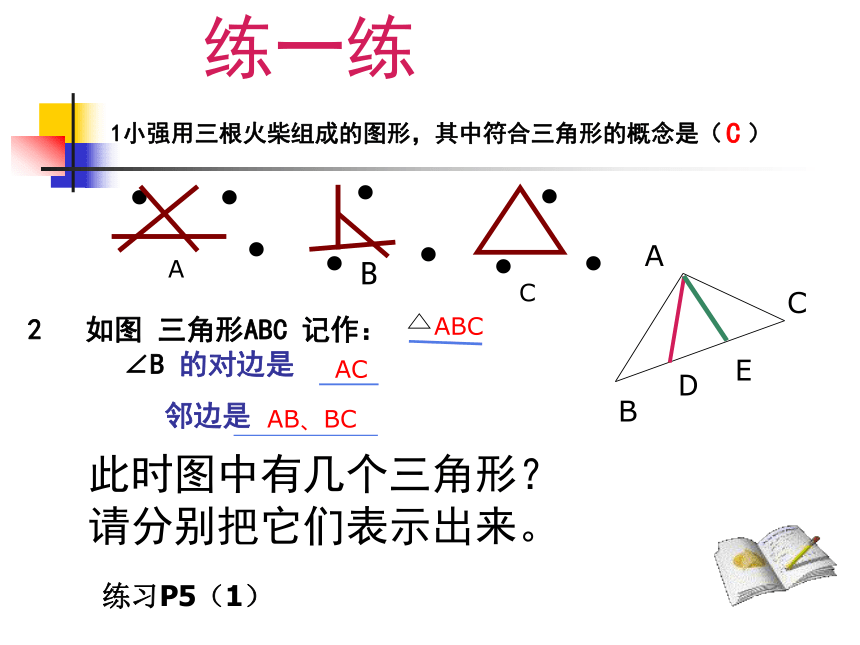
把AB（或c）、AC（或b）分别叫做 ?A 的邻边. 要素：三个内角: ∠A、∠B、∠C三个顶点: A、B、C 三条边：AB,AC,BC或 c,b,a此时图中有几个三角形？请分别把它们表示出来。1小强用三根火柴组成的图形，其中符合三角形的概念是（ ）练一练
ACAB、BC2 如图 三角形ABC 记作： ∠B 的对边是
邻边是
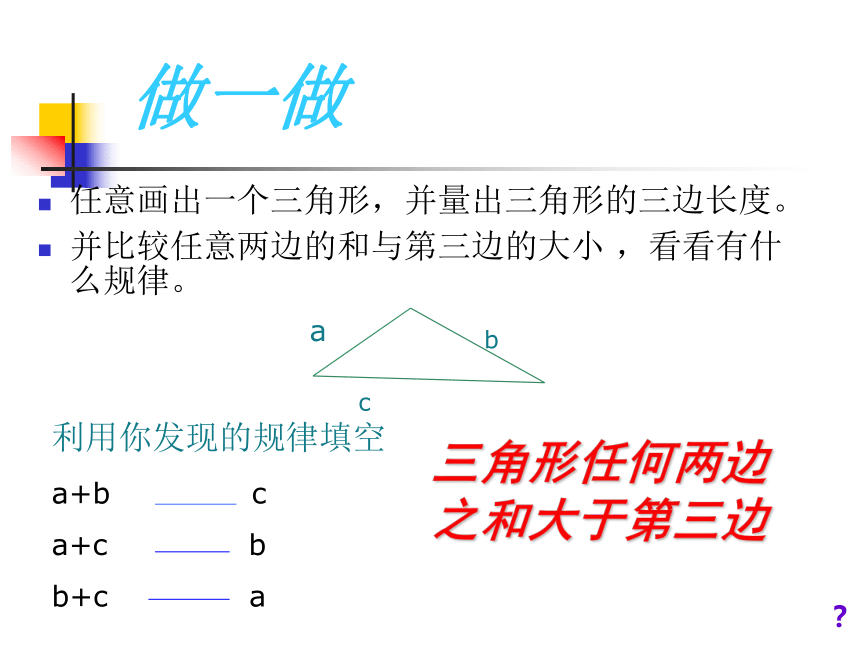
C练习P5（1）做一做任意画出一个三角形，并量出三角形的三边长度。
并比较任意两边的和与第三边的大小 ，看看有什么规律。
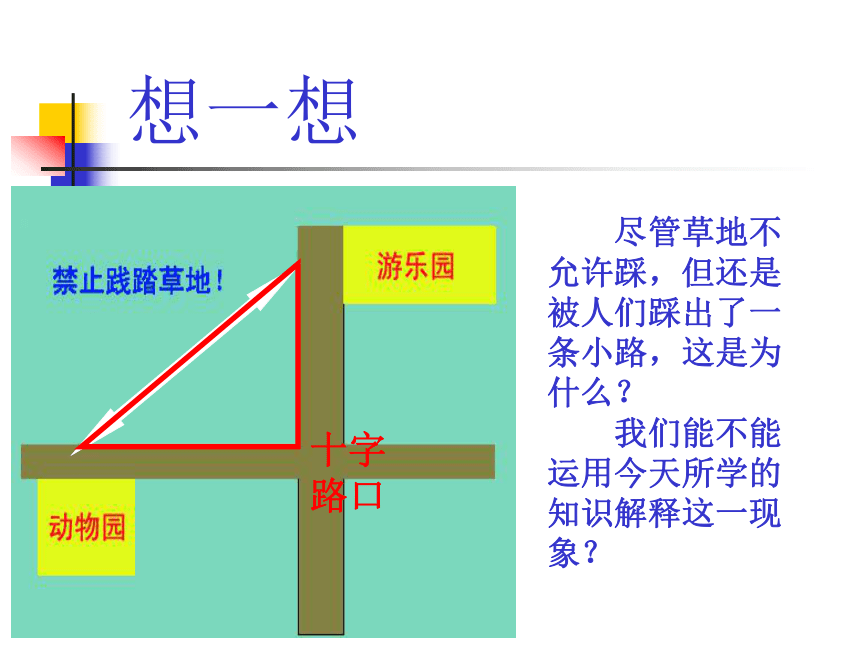
三角形任何两边之和大于第三边？想一想　　尽管草地不允许踩，但还是被人们踩出了一条小路，这是为什么？
　　我们能不能运用今天所学的知识解释这一现象？十字路口例1：判断下列各组线段中，那些能组成三角形，哪些
不能组成三角形。并说明理由
（1）a=2.5cm，b=3cm，c=5cm
（2）e=6.3cm，f=6.3cm，g=12.6cm
解： （1）∵最长线段是c=5cm，

a+b=2.5+3=5.5（cm）
∴a+b＞C 线段a，b，c能组成三角形
（2）∵最长线段g=12.6cm
e+f=6.3+6.3=12.6（cm）∴ e+f=g 线段e，f，g不能组成三角形我们知道三角形任何两边之和大于第三边，那么三角形任何两边之差与第三边有什么关系？想一想练习P5（2，3 ）有两根长度分别为5cm和8cm的木棒，现在再取一根木棒
与它们摆成一个三角形，你说第三根要多长呢？用长度为3cm的木棒行吗？为什么？用长度为14cm的木棒呢？已知三角形两边的长度，第三边长度范围是:如果告诉你：
三角形两边的长度，
第三边长度的范围你能确定吗？大于这两边的差，小于这两边的和。你想找一根多长的小棒与长为4cm。6cm的两根
小棒首尾相接组成三角形？
若三角形的周长为17，且三边长都是正整数，那么满足条件
的三角形有多少个？你可以先固定一边的长，用列表法探求探究活动：设三角形的三边为a，b，c，且a，b，c为正整数， a≥b≥c a+b+c=17 而b+c＞a ∴a≤86573645581726354所以满足条件的三角形共有8个三角形的概念
三角形的基本要素
三角形的表示方法
三角形三边之间的关系
学习了本节课你有哪些收获？四. 小结我们重点给大家介绍：1.三角形的任何两边的和大于第三边。2.已知三角形两边的长度，第三边长度范围是:大于这两边的差，小于这两边的和。请你回忆一下：AB●●②③①④上图由A地——B地，走那条路最近？为什么？