认识三角形（2）[下学期]

课件18张PPT。1.1 认识三角形(2)
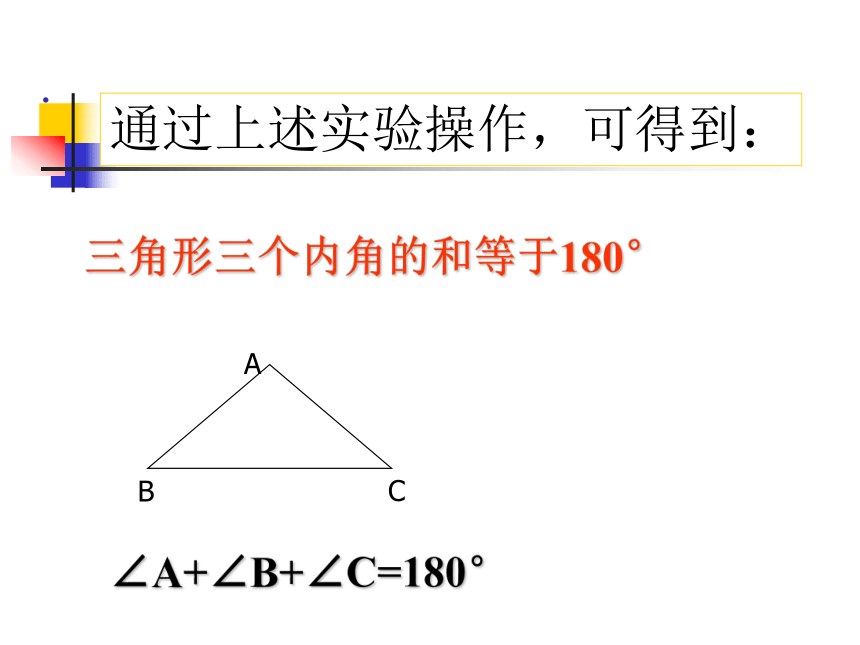
三角形任何两边之和大于第三边

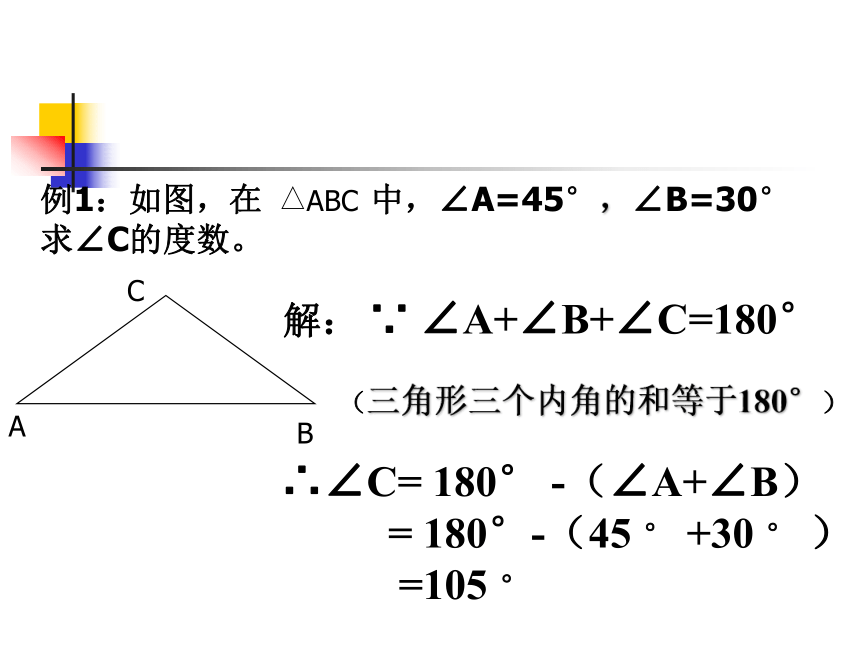
三角形任何两边之差小于第三边即：a-b求∠C的度数。CAB解： ∵ ∠A+∠B+∠C=180°（三角形三个内角的和等于180°）∴∠C= 180° -（∠A+∠B）
= 180°-（45 ° +30 ° ）
=105 ° 变式1：在三角形ABC中，∠A=45°，
∠B= 2∠C，求∠B、 ∠C的度数。
变式2：在三角形ABC中，∠A=∠B=
2∠C，求∠B、 ∠C的度数。
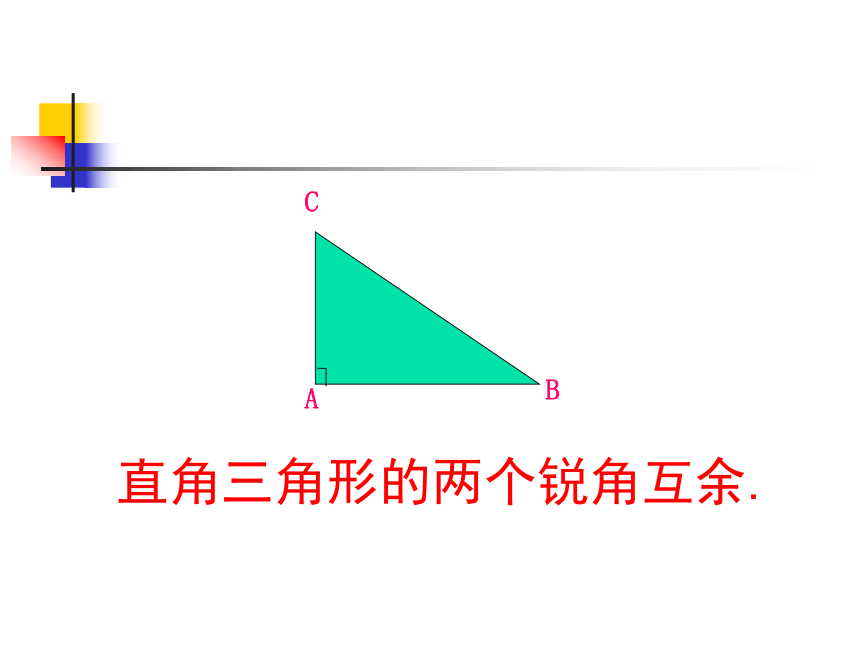
三角形按角的大小分类如下：三角形直角三角形（有一个直角）锐角三角形（三个都是锐角）钝角三角形（有一个钝角）　　直角三角形可以用符号“Rt△”表示,直角三角形ABC可以写成“Rt△ABC” 直角三角形的两个锐角互余.ABC　　三角形的一边与另一边的延长线组成的角叫做三角形的外角。ＡＢＣＤ例如上图中的∠ＡＣＤ 做一做：书本7页　　由三角形内角和性质，我们还可以有以下两个结论：1：　三角形的一个外角等于和它不相邻的两个内角的和。2：　三角形的一个外角大于任何一个和它不相邻的内角。例如上图中, ∠ACD＝∠A＋∠Ｂ ∠ACD＞∠A； ∠ACD＞∠Ｂ
例2：一把椅子的结构如图， ∠1=∠2当椅面水平时， ∠3=100°，此时∠1的度数是多少？解： ∵ ∠3是△ABC的一个外角∴∠3= ∠1+∠2（三角形的一个外角等于和它不相邻的两个内角的和）∵ ∠1=∠2∴ ∠3= 2∠1∴ ∠1= ∠2
= 1/2∠3=1/2×100 °
=50 °例3.已知如图：∠ＢＡＦ、∠ＣＢＤ、
∠ＡＣＥ是△ＡＢＣ的三个外角。
说明：∠ＢＡＦ＋∠ＣＢＤ＋∠ＡＣＥ＝３６０0解：如图， Ｆ∵ ∠ＢＡＦ＝∠２＋∠３， ∠ＣＢＤ＝∠１＋∠３，∠ＡＣＥ＝∠１＋∠２ （三角形的一个外角等于和它不相邻的两个内角的和）∴∠ＢＡＦ＋∠ＣＢＤ＋∠ＡＣＥ
＝（∠２＋∠３＋∠１＋∠３＋∠１＋∠２）＝２（∠１＋∠２＋∠３） ∵∠１＋∠２＋∠３＝１８０o（三角形的三个内角的和等于１８０o） ∴∠ＢＡＦ＋∠ＣＢＤ＋∠ＡＣＥ＝２×１８０o＝３６０o 由上述解答可知：三角形的外角和为360 o１、在△ABC中∠A：∠B：∠C＝１：２：3，则 △ABC是（ ）A 锐角三角形 B 直角三角形
C 钝角三角形 D 不能确定２、已知△ABC中，∠A∶∠B∶∠C=1∶3∶5，求∠A、∠B和∠C的度数，它是什么三角形？
B３、判断：
（1）一个三角形的三个内角可以都小于60°； 　　　　　　　　（ ）
（2）一个三角形最多只能有一个内角是钝角或直角； 　　　　　　　　　（ ）
４、在△ABC中，
（1）∠C=70°，∠A=50°，则∠B= 度；
（2）∠B=100°，∠A=∠C，则∠C= 度．√×6040 ５、如下图，在 Rt△CDE,　∠C和∠E的关系是 ，其中∠C=55°，则∠E= 度

６、如上图， 在Rt△ABC中，∠A=2∠B，则∠A= 度，∠B= 度； 互余356030三角形的内角和性质
三角形的外角性质
三角形的分类学习了本节课你有哪些收获？