5.5 一次函数的简单应用（2）

课件20张PPT。5.5一次函数图象的应用（2）XYO归纳：
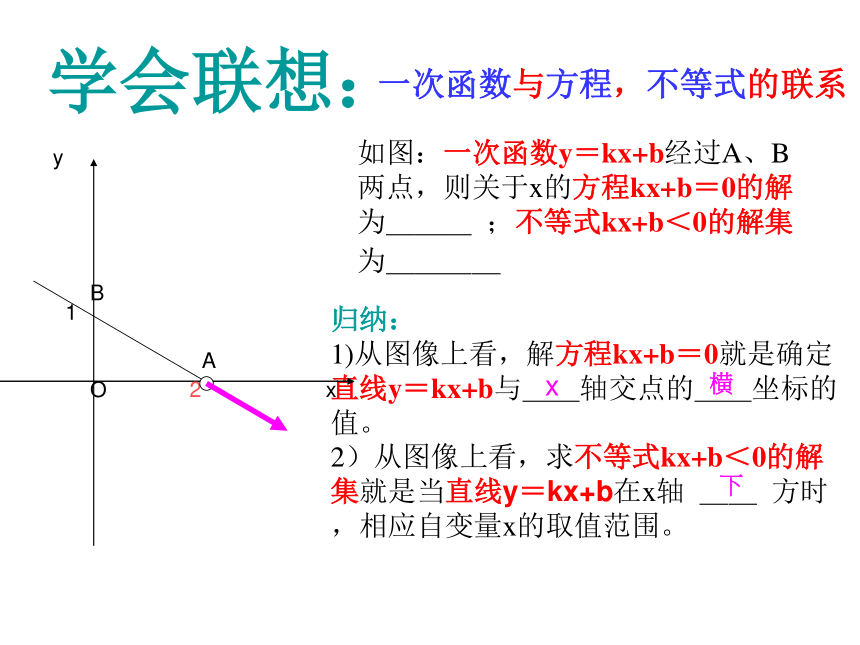
1)从图像上看，解方程kx+b＝0就是确定直线y＝kx+b与＿＿轴交点的＿＿坐标的值。
2）从图像上看，求不等式kx+b＜0的解集就是当直线y＝kx+b在x轴 ＿＿ 方时，相应自变量x的取值范围。
学会联想：如图：一次函数y＝kx+b经过A、B两点，则关于x的方程kx+b＝0的解为＿＿＿ ；不等式kx+b＜0的解集为＿＿＿＿
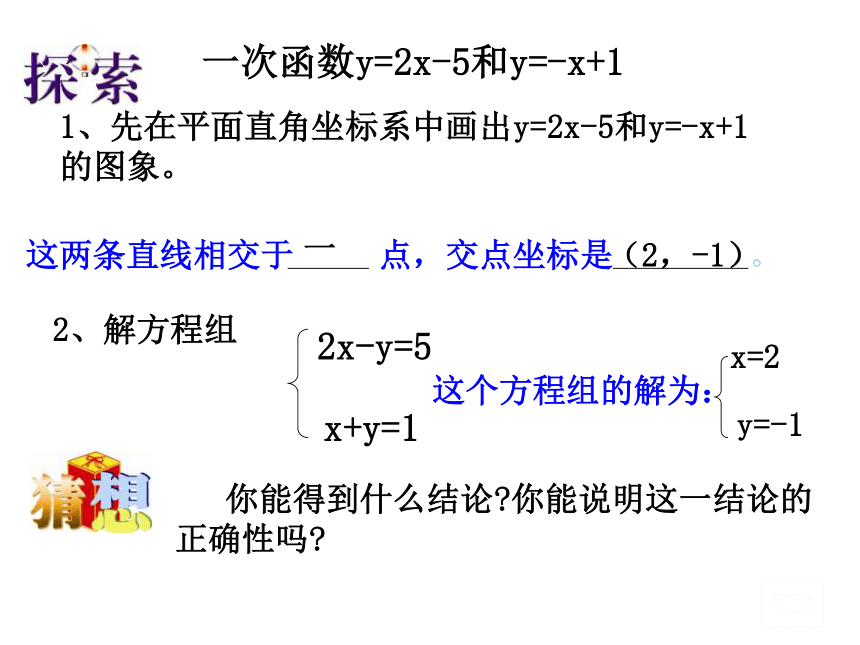
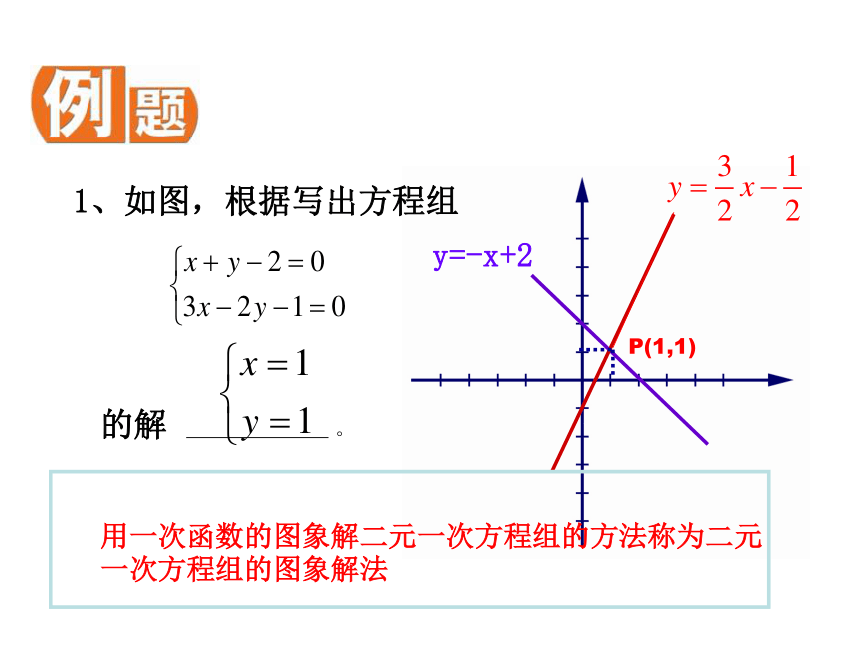
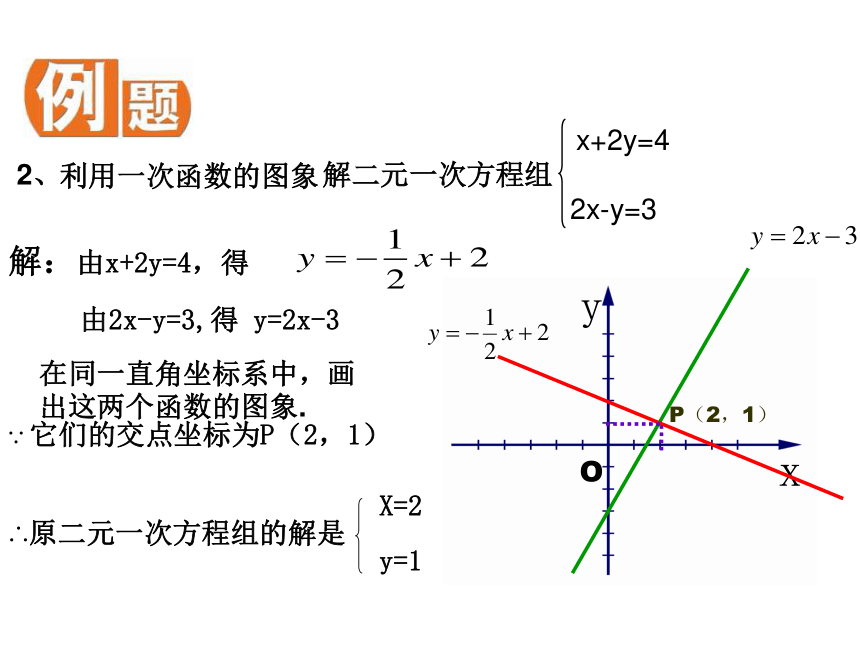
一次函数与方程，不等式的联系x横下一次函数y=2x-5和y=-x+11、先在平面直角坐标系中画出y=2x-5和y=-x+1的图象。这两条直线相交于 点，交点坐标是 。一（2，-1）2、解方程组2x-y=5x+y=1这个方程组的解为：x=2y=-1 你能得到什么结论?你能说明这一结论的正确性吗?P(1,1)y=-x+21、如图，根据写出方程组的解 。用一次函数的图象解二元一次方程组的方法称为二元一次方程组的图象解法 x+2y=4
2、 解二元一次方程组
2x-y=3
解：由x+2y=4，得 由2x-y=3,得 y=2x-3 在同一直角坐标系中，画出这两个函数的图象.P（2，1）
X=2
∴原二元一次方程组的解是
y=1
∵ 它们的交点坐标为P（2，1）利用一次函数的图象因为方程组 的解是
所以一次函数y=－x＋4与y=2x＋1的图象交点坐标
为 ． 13（1，3） 不画函数的图象，求一次函数y＝x＋3与y＝－3x－1的图象的交点坐标。就是解方程组的解。一次函数y=3x-4和 的图象之间有何关系？
一次函数y=–2x+2，y=–2x+5的图象之间有何关系？

方程组 有 解。
你能从中“悟”出些什么吗？那么，方程组 有 个解。1无(1)如果一次函数的图象平行（无交点），那么二元一次方程组
无解。
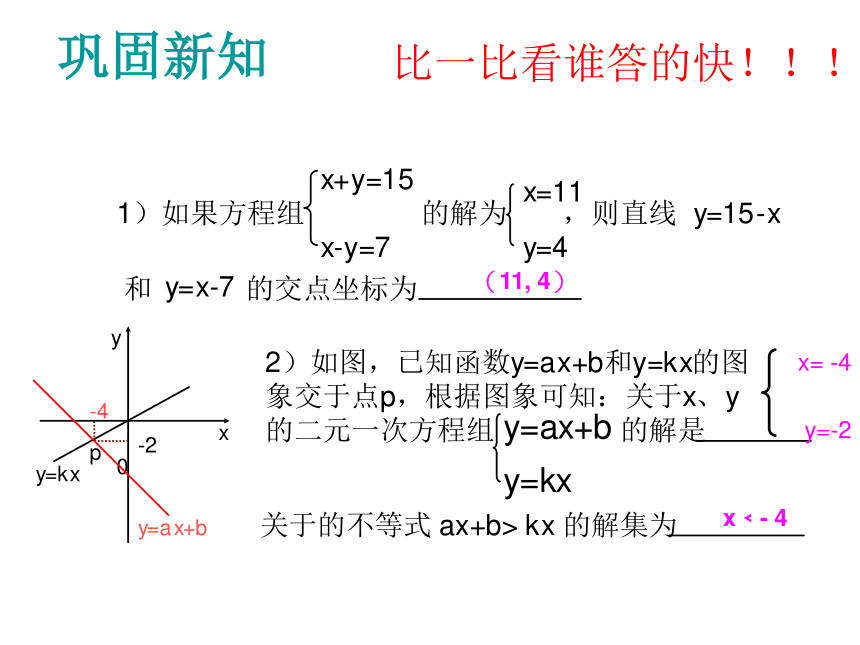
(2)如果一次函数的图象相交（有一个交点），那么二元一次方程组有一解。相交平行巩固新知比一比看谁答的快！！！
（11, 4）x= -4y=-2x﹤- 4(1)?当小聪追上小慧时，他们是否已经过了“草甸“？例3:小聪和小慧去某风景区游览，约好在“飞瀑”见面。上午7:00，小聪乘电动汽车从“古刹”出发，沿景区公路去“飞瀑”，车速为30km/h。小慧也于上午7:00从“塔林”出发，骑电动自行车沿景区公路去“飞瀑” ，车速为20km/h。（2）当小聪到达“飞瀑”时，小慧离“飞瀑”还有多少km？小聪小慧
（1）当小聪追上小慧时，他们是否已经过了“草甸”？
（2）当小聪到达“飞瀑”时，小慧离“飞瀑”还有多少km？解：设经过t时，小聪与小慧离“古刹”的路程分别为S1、S2，
由题意得：S1=30t， S2=20t+10将这两个函数解析式画在同一个直角坐标系上，观察图象，得⑴两条直线S1=36t， S2=26t+10的交点坐标为（1，30）这说明当小聪追上小慧时，S1=S2=30 km，即离“古刹”30km，小于35km，也就是说，他们还没有到“草甸”小聪小慧45-40=5（km)例3. 如图，l1反映了某公司产品的销售收入与销售量的关系，（1）当销售量为2吨时，销售收入＝　　　　元，
　　　销售成本＝　　　　元；20003000　　　　l2反映了该公司产品的销售成本与销售量的关系，根据图意填空：●●销售收入销售成本（2）当销售量为6吨时，销售收入＝　　　　元，
　　　销售成本＝　　　　元；60005000（3）当销售量为　　时，销售收入等于销售成本；4吨●●销售收入销售成本（4）当销售量　　　　时，该公司赢利（收入大于成本）；
　　当销售量　　　　时，该公司亏损（收入小于成本）；大于4吨小于4吨（5） l1对应的函数表达式是　　　　　　　　，
　　 l2对应的函数表达式是　　　　　　　　。y=1000xy=500x+2000●●销售收入销售成本(6）你能得出每吨产品的销价吗?(7）销售收入为5000元时,该公司卖出了多少吨产品? (每吨1000元)共花费了多少成本?(5吨)(4500元)你会做吗?试试看●●销售成本销售收入（1）说出甲、乙两物体的初始位置，并说明开始时谁前谁后？例2 :已知甲、乙两物体沿同一条直线同时、同向匀速运动，它们所经过的路程s与所需时间t之间的关系如图所示.（2）分别求出甲、乙的路程s关于时间t的函数解析式.甲物体在离起点2米处，乙物体在起点。甲在前乙在后.例2 :已知甲、乙两物体沿同一条直线同时、同向匀速运动，它们所经过的路程s与所需时间t之间的关系如图所示.（3）求出两直线的交点坐标，并说明实际意义.2秒时乙物体追上甲物体，它们各运动了3米。2秒前甲先乙后，2秒后乙先甲后。 （2，3）（1）一次函数与二元一次方程组可以相互转化，从图像到关系式都是完美的统一。（2）将二元一次方程组转化为两个一次函数，如果两个一次函数的图象有一个交点，那么这个交点的坐标就是这个二元一次方程组的解。