1.1 认识三角形(1)[下学期]

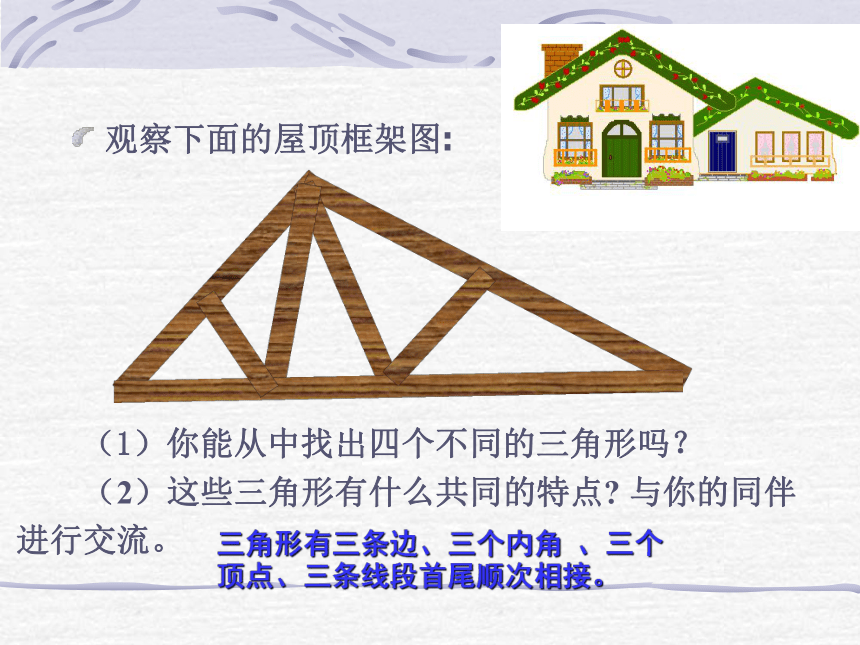
课件19张PPT。1.1 认识三角形　1、如何表示线段、射线和直线？2、如何表示一个角？复习回顾观察下面的屋顶框架图: （2）这些三角形有什么共同的特点? 与你的同伴进行交流。 （1）你能从中找出四个不同的三角形吗？三角形有三条边、三个内角 、三个
顶点、三条线段首尾顺次相接。三角形的概念:由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形（triangle）。每一个三角形都有三条边:AB、BC、CA, 三个内角: ?A 、 ?B 、 ?C

三角形的表示:三角形可以用符号“?”表示，如图顶点是A,B,C的三角形，记作“?ABC”,读做“三角形ABC”.它的三边有时也用a,b,c来表示。如图，顶点A所对的边用a表示，边CA 、 AB分别用来b 、 c表示．ABC注意:表示三角形时，字母没有先后顺序.
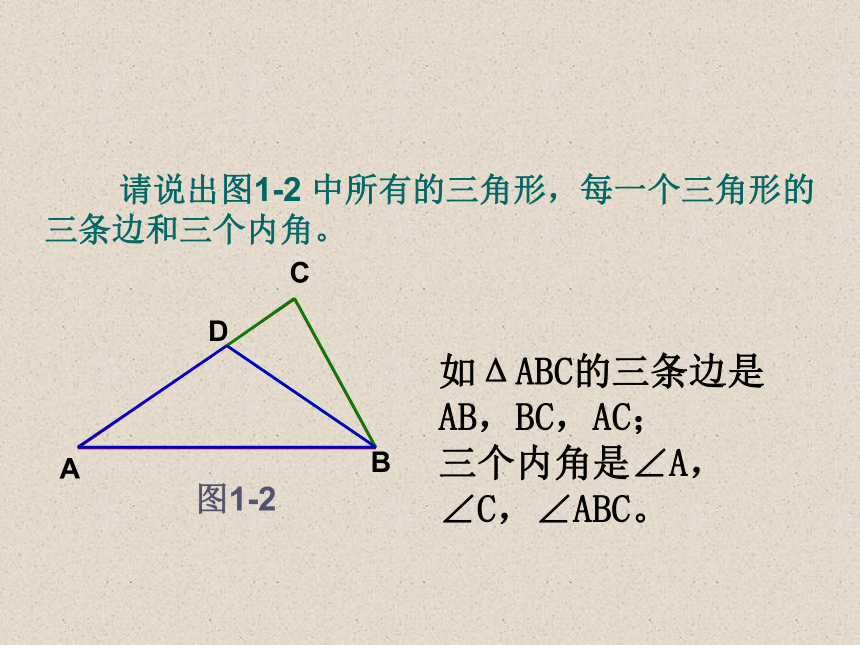
图1-2 请说出图1-2 中所有的三角形，每一个三角形的三条边和三个内角。如ΔABC的三条边是
AB，BC，AC；
三个内角是∠A，
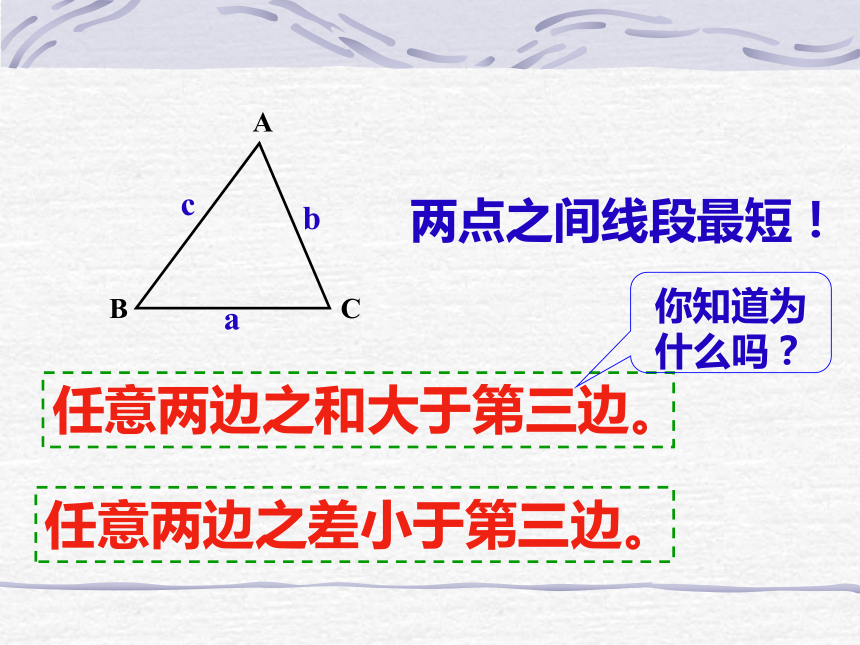
∠C，∠ABC。小组活动： (1)任意画一个三角形，量出它的三边长度，并填空：a+b____c; b+c____a; c+a____b
a-b____c; b-c____a; c-a____b
(3)通过以上的计算你认为三角形的三边存在怎样的关系？(4)请用已学过的知识解释你的结论.a=______;b=_______;c=______（2）计算并比较：任意两边之和大于第三边。任意两边之差小于第三边。ABCabc你知道为什么吗？两点之间线段最短！长度为6cm, 4cm, 3cm三条线段能否组成三角形？因为 6+4>3
6+3>4
4+3>6
所以能组成三角形.例1 判断下列各组线段中，哪些能组成三
角形，哪些不能组成三角形，并说明理由。
（1）a=2.5cm, b=3cm, c=5cm.
（2）e=6.3cm, f=6.3cm, g=12.6cm.解（1）∵ 最长线段是c=5cm,a+b=2.5+3=5.5(cm)∴ a+b＞c.线段a,b,c能组成三角形。（2）∵ 最长线段是g=12.6cm,e+f=6.3+6.3=12.6(cm)∴ e+f=g.线段e,f,g不能组成三角形。练一练1.如图，请写出：
(1)图中各三角形；
(2)每一个三角形的三条边和三个内角。2.由下列长度的三条线段能组成三角形吗?请说明理由.
(1)1cm,2cm,3.5cm (2)4cm,5cm,9cm (3)6cm,8cm,13cm 解：
　(1) ∵最长的线段3.5cm , 另两条线段1+2=3cm
∴3.5>1+2 , 线段1cm,2cm,3.5cm不能组成三角形。
　(2) ∵最长的线段9cm , 另两条线段4+5=9cm
∴9=4+5 , 线段4cm, 5cm,9cm不能组成三角形。
　(3) ∵最长的线段13cm , 另两条线段6+8=14cm
∴13>6+8 , 线段6cm,8cm,13cm能组成三角形。课内练习1.如图,请写出:
(1)图中各三角形;
(2)每一个三角形的三条边和三个内角.2.由下列长度的三条线段能组成三角形吗?请说明
理由.
(1) 1cm, 2cm, 3.5cm; (2)4cm, 5cm, 9cm;
(2) 6cm, 8cm, 13cm. 3.如图,在△ABC中,D是AB
是一点,且AD=AC,连结CD.用
“>”或“<”号填入下面各个
空格，并说明理由。
（1）2AD____CD;
(2) AB____AC + BC＞＜4. 6-5< c< 6+5 即 1（1）1cm、2cm、3.5cm
（2）4cm、5cm、9cm
（3）6cm、8cm、13cm
能组成三角形的有（ ）组。
思考题：在 ABC中，AB=7 BC=3，并且AC为奇数，那么 ABC的周长为________。1.三角形的概念
2.三角形的表示方法
3.三角形三边之间的关系
学习了本节课你有哪些收获？你知道怎样判断三条线段能否组成一个三角形？想一想：你能举出生活中应用三角形稳 定性的实例吗？三角形具有稳定性作业布置１.１认识三角形（一）谢谢大家
的合作