4.6相似多边形 课件(共26张PPT)
文档属性
| 名称 | 4.6相似多边形 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-17 17:39:01 | ||
图片预览






文档简介
(共26张PPT)
4.6相似多边形
浙教版 九年级上册
教学目标
教学目标:
1.掌握相似多边形的性质.
2.理解相似多边形的应用.
重点:相似多边形的性质以及应用.
难点:相似多边形的性质.
情景导入
观察下面神州十一号的图片,它是由其中的一幅图缩小得到的,把一个图形缩小得到的图形与原图形之间有什么关系呢?
新知探究
A
B
C
D
A1
B1
C1
D1
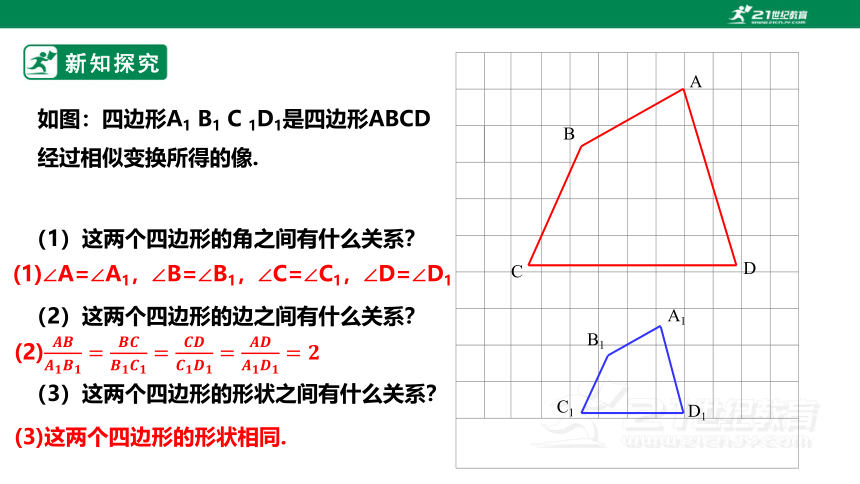
如图:四边形A1 B1 C 1D1是四边形ABCD经过相似变换所得的像.
(1)这两个四边形的角之间有什么关系?
(2)这两个四边形的边之间有什么关系?
(3)这两个四边形的形状之间有什么关系?
(1)∠A=∠A1,∠B=∠B1,∠C=∠C1,∠D=∠D1
(2)
(3)这两个四边形的形状相同.
新知探究
相似三角形:
一般地,对应角相等,对应边成比例的两个三角形,叫做相似三角形.
相似比:
相似多边形对应边的比叫做相似比.
如:四边形ABCD与四边形A1B1C1D1相似,记作四边形ABCD∽四边形A1B1C1D1,其中 AB:A1B1的值就是相似比.
2、在记两个多边形相似时,要把表示对应角顶点的字母写在对应的位置上.
注: 1、相似符号“∽ ”读作“相似于”.
新知探究
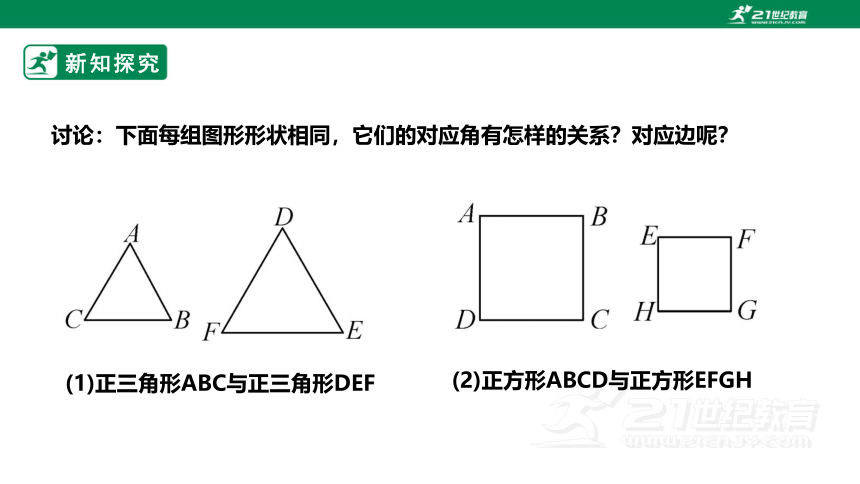
讨论:下面每组图形形状相同,它们的对应角有怎样的关系?对应边呢?
(1)正三角形ABC与正三角形DEF
(2)正方形ABCD与正方形EFGH
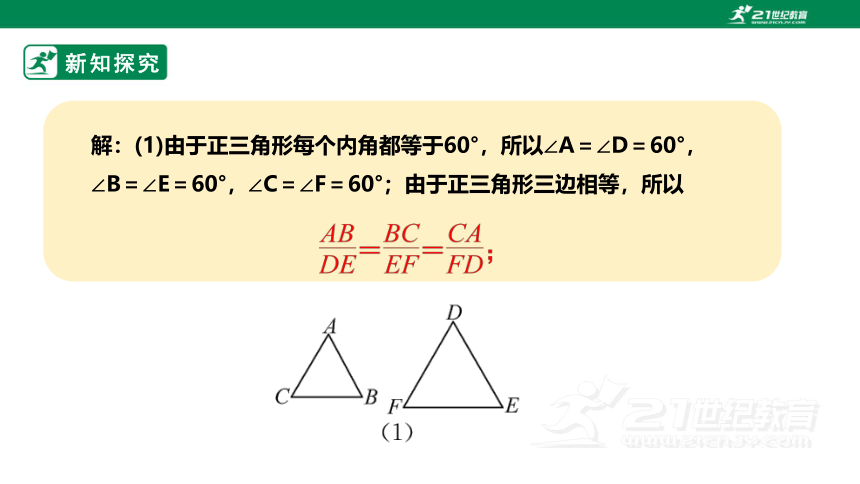
新知探究
解:(1)由于正三角形每个内角都等于60°,所以∠A=∠D=60°,∠B=∠E=60°,∠C=∠F=60°;由于正三角形三边相等,所以
新知探究
(2)由于正方形的每个角都是直角,所以∠A=∠E=90°,∠B=∠F=90°,∠C=∠G=90°,∠D=∠H=90°;由于正方形四边相等,所以
新知探究
相似多边形的特征:
相似多边形的对应边成比例,对应角相等.
新知探究
例1、矩形纸张的长与宽之比为,沿长边对折,所得的矩形纸张是否和原来的矩形纸张相似 请说明理由.
A
B
C
D
E
F
解:沿长边对折后所得的矩形纸张和原来的矩形纸张相似.理由如下:原来的纸张为矩形ABCD,.
在矩形ABFE中,
∴
即矩形ABFE与矩形BCDA的对应边成比例,而两个矩形的对应角相等,所以矩形ABFE与矩形BCDA相似.
连结BC与AD的中点F、E,则EF就把矩形ABCD分为全等的两个矩形.
新知探究
如图,四边形ABCD∽四边形A′B′C′D′,其相似比为k,试回答下面问题:
(1)四边形ABCD与四边形A′B′C′D′的周长比是______.
(2)四边形ABCD与四边形A′B′C′D′的面积比是______.
A
B
C
D
A′
B′
C′
D′
k : 1
k2 : 1
新知探究
两个相似五边形的周长比等于相似比吗?面积比等于相似比的平方吗?
两个相似的n边形呢?
无论是三角形、四边形、还是多边形,都有相同的结论,所以可以推导出:相似多边形的周长比等于相似比,面积比等于相似比的平方.
新知探究
相似多边形的特征:
相似多边形的周长之比等于相似比;
面积之比等于相似比的平方.
新知探究
如图,从四边形ABCD到四边形A’B’C’D’的改变过程中,图形的形状没有改变.
一般地,由一个图形改变为另一个图形,在改变的过程中保持形状不变,这样的图形改变叫做图形的相似.
新知探究
图形的相似在生活中有着广泛的应用,如地图的绘制,照片的放大与缩小.
课堂练习
1.放大镜中的多边形与原多边形的关系是( )
A.形状不同,大小不同 B.形状相同,大小相同
C.形状相同,大小不同 D.形状不同,大小相同
B
2.下列四组图形中,一定相似的是( )
A.正方形与矩形 B.正方形与菱形
C.菱形与菱形 D.正五边形与正五边形
D
课堂练习
3.如图所示的三个矩形中,相似的是( )
A.甲和乙 B.甲和丙
C.乙和丙 D.甲、乙和丙
B
课堂练习
4.如图所示的两个四边形相似,则α的度数是( )
A.87°
B.60°
C.75°
D.120°
A
课堂练习
5.已知△ABC和△A1B1C1相似,且相似比为2∶3;△A1B1C1和△A2B2C2相似,且相似比为5∶4,则△ABC与△A2B2C2的相似比为( )
A.5∶6
B.6∶5
C.5∶6或6∶5
D.8∶15
A
课堂练习
6.如图,△ABC∽△ACP.若∠A=75°,∠APC=65°,则∠B的度数为________.
40°
课堂练习
7. 如图,在梯形ABCD中,AD∥BC,E是AB上的一点,EF∥BC,并且EF将梯形ABCD分成的梯形AEFD和梯形EBCF相似,若AD=4,BC=9,求EF的长.
解:∵梯形AEFD∽梯形EBCF.
∴EF2=AD·BC=4×9=36,
∴EF=6.
课堂练习
8. 如图,把矩形 ABCD 对折,折痕为 EF,若矩形ABCD 与矩形 EABF 相似,AB = 1.
(1) 求BC长;
A
B
C
D
E
F
解:∵ E 是 AD 的中点,
∴ .
又∵矩形 ABCD 与矩形 EABF相似,AB=1,
∴ ,
∴ AB2 = AE·BC,
∴ ,
解得
课堂练习
(2) 求矩形 EABF与矩形 ABCD 的相似比.
A
B
C
D
E
F
解:矩形 EABF 与矩形 ABCD的相似比为:
课堂小结
相似多边形
概念:各角分别相等、各边成比例的两个多边形叫做
相似多边形.
性质:相似多边形的对应角相等,对应边成比例.
相似多边形的周长之比等于相似比;
面积之比等于相似比的平方.
相似比:相似多边形对应边的比叫做相似比.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
4.6相似多边形
浙教版 九年级上册
教学目标
教学目标:
1.掌握相似多边形的性质.
2.理解相似多边形的应用.
重点:相似多边形的性质以及应用.
难点:相似多边形的性质.
情景导入
观察下面神州十一号的图片,它是由其中的一幅图缩小得到的,把一个图形缩小得到的图形与原图形之间有什么关系呢?
新知探究
A
B
C
D
A1
B1
C1
D1
如图:四边形A1 B1 C 1D1是四边形ABCD经过相似变换所得的像.
(1)这两个四边形的角之间有什么关系?
(2)这两个四边形的边之间有什么关系?
(3)这两个四边形的形状之间有什么关系?
(1)∠A=∠A1,∠B=∠B1,∠C=∠C1,∠D=∠D1
(2)
(3)这两个四边形的形状相同.
新知探究
相似三角形:
一般地,对应角相等,对应边成比例的两个三角形,叫做相似三角形.
相似比:
相似多边形对应边的比叫做相似比.
如:四边形ABCD与四边形A1B1C1D1相似,记作四边形ABCD∽四边形A1B1C1D1,其中 AB:A1B1的值就是相似比.
2、在记两个多边形相似时,要把表示对应角顶点的字母写在对应的位置上.
注: 1、相似符号“∽ ”读作“相似于”.
新知探究
讨论:下面每组图形形状相同,它们的对应角有怎样的关系?对应边呢?
(1)正三角形ABC与正三角形DEF
(2)正方形ABCD与正方形EFGH
新知探究
解:(1)由于正三角形每个内角都等于60°,所以∠A=∠D=60°,∠B=∠E=60°,∠C=∠F=60°;由于正三角形三边相等,所以
新知探究
(2)由于正方形的每个角都是直角,所以∠A=∠E=90°,∠B=∠F=90°,∠C=∠G=90°,∠D=∠H=90°;由于正方形四边相等,所以
新知探究
相似多边形的特征:
相似多边形的对应边成比例,对应角相等.
新知探究
例1、矩形纸张的长与宽之比为,沿长边对折,所得的矩形纸张是否和原来的矩形纸张相似 请说明理由.
A
B
C
D
E
F
解:沿长边对折后所得的矩形纸张和原来的矩形纸张相似.理由如下:原来的纸张为矩形ABCD,.
在矩形ABFE中,
∴
即矩形ABFE与矩形BCDA的对应边成比例,而两个矩形的对应角相等,所以矩形ABFE与矩形BCDA相似.
连结BC与AD的中点F、E,则EF就把矩形ABCD分为全等的两个矩形.
新知探究
如图,四边形ABCD∽四边形A′B′C′D′,其相似比为k,试回答下面问题:
(1)四边形ABCD与四边形A′B′C′D′的周长比是______.
(2)四边形ABCD与四边形A′B′C′D′的面积比是______.
A
B
C
D
A′
B′
C′
D′
k : 1
k2 : 1
新知探究
两个相似五边形的周长比等于相似比吗?面积比等于相似比的平方吗?
两个相似的n边形呢?
无论是三角形、四边形、还是多边形,都有相同的结论,所以可以推导出:相似多边形的周长比等于相似比,面积比等于相似比的平方.
新知探究
相似多边形的特征:
相似多边形的周长之比等于相似比;
面积之比等于相似比的平方.
新知探究
如图,从四边形ABCD到四边形A’B’C’D’的改变过程中,图形的形状没有改变.
一般地,由一个图形改变为另一个图形,在改变的过程中保持形状不变,这样的图形改变叫做图形的相似.
新知探究
图形的相似在生活中有着广泛的应用,如地图的绘制,照片的放大与缩小.
课堂练习
1.放大镜中的多边形与原多边形的关系是( )
A.形状不同,大小不同 B.形状相同,大小相同
C.形状相同,大小不同 D.形状不同,大小相同
B
2.下列四组图形中,一定相似的是( )
A.正方形与矩形 B.正方形与菱形
C.菱形与菱形 D.正五边形与正五边形
D
课堂练习
3.如图所示的三个矩形中,相似的是( )
A.甲和乙 B.甲和丙
C.乙和丙 D.甲、乙和丙
B
课堂练习
4.如图所示的两个四边形相似,则α的度数是( )
A.87°
B.60°
C.75°
D.120°
A
课堂练习
5.已知△ABC和△A1B1C1相似,且相似比为2∶3;△A1B1C1和△A2B2C2相似,且相似比为5∶4,则△ABC与△A2B2C2的相似比为( )
A.5∶6
B.6∶5
C.5∶6或6∶5
D.8∶15
A
课堂练习
6.如图,△ABC∽△ACP.若∠A=75°,∠APC=65°,则∠B的度数为________.
40°
课堂练习
7. 如图,在梯形ABCD中,AD∥BC,E是AB上的一点,EF∥BC,并且EF将梯形ABCD分成的梯形AEFD和梯形EBCF相似,若AD=4,BC=9,求EF的长.
解:∵梯形AEFD∽梯形EBCF.
∴EF2=AD·BC=4×9=36,
∴EF=6.
课堂练习
8. 如图,把矩形 ABCD 对折,折痕为 EF,若矩形ABCD 与矩形 EABF 相似,AB = 1.
(1) 求BC长;
A
B
C
D
E
F
解:∵ E 是 AD 的中点,
∴ .
又∵矩形 ABCD 与矩形 EABF相似,AB=1,
∴ ,
∴ AB2 = AE·BC,
∴ ,
解得
课堂练习
(2) 求矩形 EABF与矩形 ABCD 的相似比.
A
B
C
D
E
F
解:矩形 EABF 与矩形 ABCD的相似比为:
课堂小结
相似多边形
概念:各角分别相等、各边成比例的两个多边形叫做
相似多边形.
性质:相似多边形的对应角相等,对应边成比例.
相似多边形的周长之比等于相似比;
面积之比等于相似比的平方.
相似比:相似多边形对应边的比叫做相似比.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
