3.8.2弧长及扇形的面积 课件(共24张PPT)
文档属性
| 名称 | 3.8.2弧长及扇形的面积 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-17 17:47:21 | ||
图片预览






文档简介
3.8.2弧长及扇形的面积
浙教版 九年级上册
教学目标
教学目标:
经历探索扇形面积计算公式的过程.
重点:扇形面积计算公式.
难点:扇形面积计算公式的推导.
什么样的图形叫做扇形?
O ●
由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形.
半径
半径
弧
圆心角
扇形
扇形是圆的一部分
A
B
定义
O
A
B
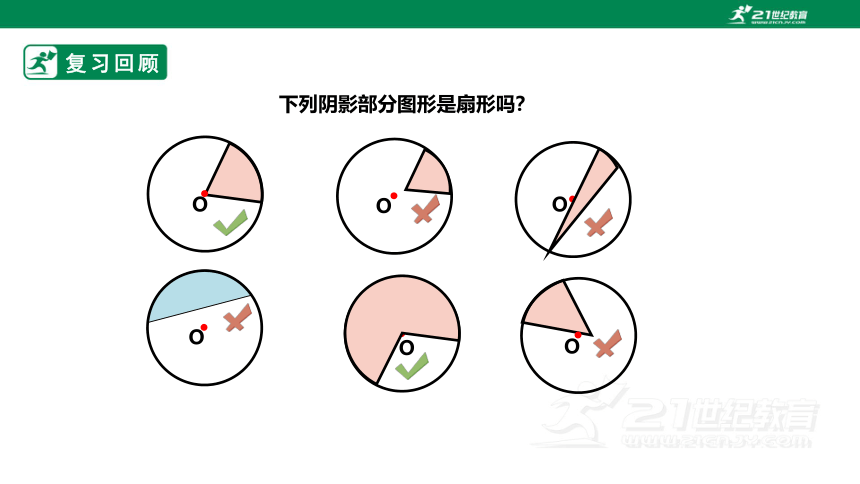
复习回顾
下列阴影部分图形是扇形吗?
O
O
O
O
O
O
复习回顾
情景导入
在一块空旷的草地上有一根柱子,柱子上栓着一条长3m的绳子,绳子的一端栓着一只狗.
(1)这只狗的最大活动区域有多大?
πr2 = 9π m2
半径为 3m 的圆的面积
情景导入
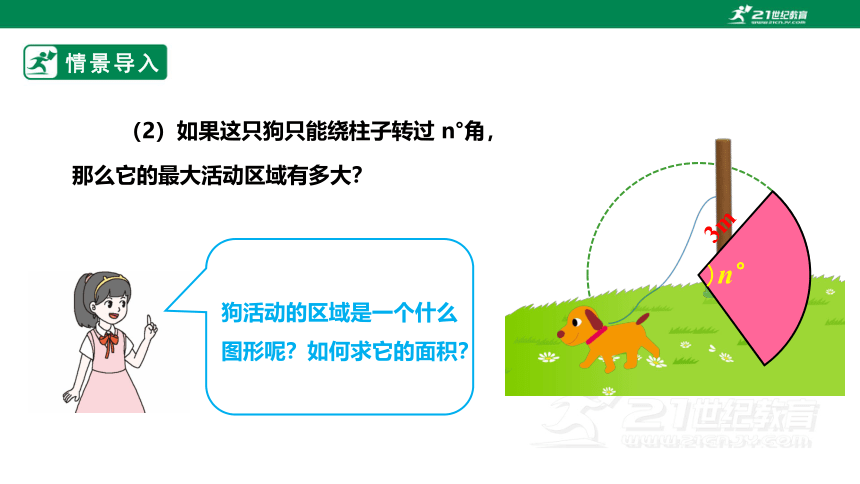
(2)如果这只狗只能绕柱子转过 n°角,
那么它的最大活动区域有多大?
n°
3m
狗活动的区域是一个什么图形呢?如何求它的面积?
新知探究
类比弧长公式的推导,如何推导扇形的面积公式?
(1)半径为R的圆,面积是多少?
(2)圆的面积可以看作多少度的圆心角所对的弧长?
(3)1°的圆心角所对的扇形面积是多少?
(4)n°的圆心角所对的面积是多少?
(5)由此不难得出:半径是R,所对圆心角是n°的扇形的面积是多少?
360°
问题
归纳总结
半径为r的圆中,圆心角为n°的扇形的面积
①公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;
②公式要理解记忆(即按照上面推导过程记忆).
注意
扇形面积公式:
新知探究
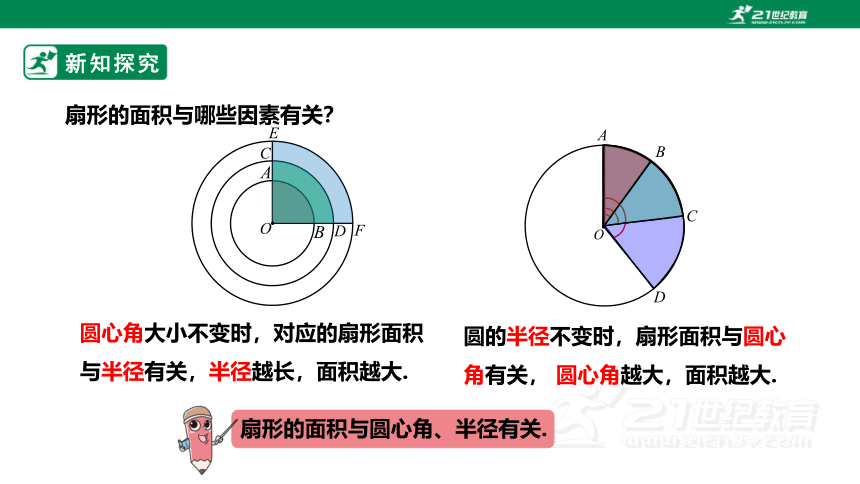
圆心角大小不变时,对应的扇形面积与半径有关,半径越长,面积越大.
圆的半径不变时,扇形面积与圆心角有关, 圆心角越大,面积越大.
扇形的面积与哪些因素有关?
O
A
B
D
C
E
F
●
O
A
B
C
D
●
扇形的面积与圆心角、半径有关.
新知探究
问题 扇形的弧长公式与面积公式有联系吗?
想一想 :扇形的面积公式与什么公式类似?
A
B
O
O
例题讲解
例3 如图,有一把折扇和一把团扇。已知折扇的骨柄与团扇的直径一样长,折扇扇面的宽度是骨柄长的一半,折扇张开的角度为120 °,问哪一把扇子扇面的面积大?
解:设折扇的骨柄长为a,由于折扇扇面面积为两个扇形面积之差,
所以两把扇子扇面的面积一样大.
∴????折扇=??????????????????????????????????????????????????????????????????×????????????=????????????????
?
而????团扇=????×????????????=????????????????
?
例题讲解
例4 我国著名的引滦工程的主干线输水管的直径为2.5m,设计流量为12.73????????/????.如果水管截面中水面面积如图所示,其中∠AOB=45°,那么水的流速应达到每秒多少米(精确到0.01m/s)?
?
例题讲解
解:∵ 输水管的直径为2.5m
OB=OA=????????????
∵ ∠AOB=45°,BD⊥OA
∴OD=OB
∴OB=????????????
?
则?????????????????=?????????????????????????=????????×????????×????????×????????=????????????????????
?
新知探究
?
由弦及弦所对的弧组成的图形叫做弓形.
1.在圆心角为120°的扇形AOB中,半径OA=6 cm,则扇形AOB的面积是( )
A.6π cm2 B.8π cm2
C.12π cm2 D.24π cm2
C
2.已知⊙O的半径OA= ,扇形OAB的面积为15π,则
所对的圆心角是( )
A.120° B.72° C.36° D.60°
B
AB
(
课堂练习
1.如果一个扇形的弧长等于它的半径,那么此扇形称为“等边扇形”,那么半径为2的“等边扇形”的面积为( )
A.π B.1 C.2 D.
2.如图,直径AB为6的半圆,绕点A逆时针旋转60°,此时点B到了点B′,则图中阴影部分的面积是( )
A.6π B.5π C.4π D.3π
C
A
课堂练习
3.一个扇形的圆心角是120°,面积是3π cm2,那么这个扇形的半径是( )
A.1 cm B.3 cm C.6 cm D.9 cm
B
4. 如图,某数学兴趣小组将边长为3的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形DAB的面积为( )
A.6 B.7 C.8 D.9
D
课堂练习
5.如图,⊙A、 ⊙B、 ⊙C、 ⊙D两两不相交,且半径都是2cm,则图中阴影部分的面积是 .
A
B
C
D
课堂练习
6.如图,AB为⊙O的直径,点C,D在⊙O上,且BC=6 cm,AC=8 cm,∠ABD=45°.
(1)求BD的长;(2)求图中阴影部分的面积.
解 :(1)∵AB为⊙O的直径,
∴∠ACB=90°.
∵BC=6 cm,AC=8 cm,
∴AB=10 cm,∴OB=5 cm.
连接OD.
∵OD=OB,
∴∠ODB=∠ABD=45°,
∴∠BOD=90°,
(2)S阴影=S扇形-S△OBD
=???????????????????? π·52- ?????????×5×5
?
= (cm2).
25π-50
4
∴BD2=OB2+OD2, BD= cm.
课堂练习
7.如图,有一直径是20cm的圆形纸片,现从中剪出一个圆心角是90°的扇形ABC,求被剪掉部分的面积.
解:连接BC,∵∠BAC=90°,
∴BC是⊙O的直径,
∴BC=20cm,
∵AB=AC,
∴AB=AC=
即被剪掉部分的面积为50πcm2.
课堂练习
8.如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.9cm,求截面上有水部分的面积.
O
A
B
D
C
E
解:
课堂小结
扇形面积公式:
在半径为R的圆中,n°的圆心角所对的扇形面积为 .
S扇形= ????
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
浙教版 九年级上册
教学目标
教学目标:
经历探索扇形面积计算公式的过程.
重点:扇形面积计算公式.
难点:扇形面积计算公式的推导.
什么样的图形叫做扇形?
O ●
由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形.
半径
半径
弧
圆心角
扇形
扇形是圆的一部分
A
B
定义
O
A
B
复习回顾
下列阴影部分图形是扇形吗?
O
O
O
O
O
O
复习回顾
情景导入
在一块空旷的草地上有一根柱子,柱子上栓着一条长3m的绳子,绳子的一端栓着一只狗.
(1)这只狗的最大活动区域有多大?
πr2 = 9π m2
半径为 3m 的圆的面积
情景导入
(2)如果这只狗只能绕柱子转过 n°角,
那么它的最大活动区域有多大?
n°
3m
狗活动的区域是一个什么图形呢?如何求它的面积?
新知探究
类比弧长公式的推导,如何推导扇形的面积公式?
(1)半径为R的圆,面积是多少?
(2)圆的面积可以看作多少度的圆心角所对的弧长?
(3)1°的圆心角所对的扇形面积是多少?
(4)n°的圆心角所对的面积是多少?
(5)由此不难得出:半径是R,所对圆心角是n°的扇形的面积是多少?
360°
问题
归纳总结
半径为r的圆中,圆心角为n°的扇形的面积
①公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;
②公式要理解记忆(即按照上面推导过程记忆).
注意
扇形面积公式:
新知探究
圆心角大小不变时,对应的扇形面积与半径有关,半径越长,面积越大.
圆的半径不变时,扇形面积与圆心角有关, 圆心角越大,面积越大.
扇形的面积与哪些因素有关?
O
A
B
D
C
E
F
●
O
A
B
C
D
●
扇形的面积与圆心角、半径有关.
新知探究
问题 扇形的弧长公式与面积公式有联系吗?
想一想 :扇形的面积公式与什么公式类似?
A
B
O
O
例题讲解
例3 如图,有一把折扇和一把团扇。已知折扇的骨柄与团扇的直径一样长,折扇扇面的宽度是骨柄长的一半,折扇张开的角度为120 °,问哪一把扇子扇面的面积大?
解:设折扇的骨柄长为a,由于折扇扇面面积为两个扇形面积之差,
所以两把扇子扇面的面积一样大.
∴????折扇=??????????????????????????????????????????????????????????????????×????????????=????????????????
?
而????团扇=????×????????????=????????????????
?
例题讲解
例4 我国著名的引滦工程的主干线输水管的直径为2.5m,设计流量为12.73????????/????.如果水管截面中水面面积如图所示,其中∠AOB=45°,那么水的流速应达到每秒多少米(精确到0.01m/s)?
?
例题讲解
解:∵ 输水管的直径为2.5m
OB=OA=????????????
∵ ∠AOB=45°,BD⊥OA
∴OD=OB
∴OB=????????????
?
则?????????????????=?????????????????????????=????????×????????×????????×????????=????????????????????
?
新知探究
?
由弦及弦所对的弧组成的图形叫做弓形.
1.在圆心角为120°的扇形AOB中,半径OA=6 cm,则扇形AOB的面积是( )
A.6π cm2 B.8π cm2
C.12π cm2 D.24π cm2
C
2.已知⊙O的半径OA= ,扇形OAB的面积为15π,则
所对的圆心角是( )
A.120° B.72° C.36° D.60°
B
AB
(
课堂练习
1.如果一个扇形的弧长等于它的半径,那么此扇形称为“等边扇形”,那么半径为2的“等边扇形”的面积为( )
A.π B.1 C.2 D.
2.如图,直径AB为6的半圆,绕点A逆时针旋转60°,此时点B到了点B′,则图中阴影部分的面积是( )
A.6π B.5π C.4π D.3π
C
A
课堂练习
3.一个扇形的圆心角是120°,面积是3π cm2,那么这个扇形的半径是( )
A.1 cm B.3 cm C.6 cm D.9 cm
B
4. 如图,某数学兴趣小组将边长为3的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形DAB的面积为( )
A.6 B.7 C.8 D.9
D
课堂练习
5.如图,⊙A、 ⊙B、 ⊙C、 ⊙D两两不相交,且半径都是2cm,则图中阴影部分的面积是 .
A
B
C
D
课堂练习
6.如图,AB为⊙O的直径,点C,D在⊙O上,且BC=6 cm,AC=8 cm,∠ABD=45°.
(1)求BD的长;(2)求图中阴影部分的面积.
解 :(1)∵AB为⊙O的直径,
∴∠ACB=90°.
∵BC=6 cm,AC=8 cm,
∴AB=10 cm,∴OB=5 cm.
连接OD.
∵OD=OB,
∴∠ODB=∠ABD=45°,
∴∠BOD=90°,
(2)S阴影=S扇形-S△OBD
=???????????????????? π·52- ?????????×5×5
?
= (cm2).
25π-50
4
∴BD2=OB2+OD2, BD= cm.
课堂练习
7.如图,有一直径是20cm的圆形纸片,现从中剪出一个圆心角是90°的扇形ABC,求被剪掉部分的面积.
解:连接BC,∵∠BAC=90°,
∴BC是⊙O的直径,
∴BC=20cm,
∵AB=AC,
∴AB=AC=
即被剪掉部分的面积为50πcm2.
课堂练习
8.如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.9cm,求截面上有水部分的面积.
O
A
B
D
C
E
解:
课堂小结
扇形面积公式:
在半径为R的圆中,n°的圆心角所对的扇形面积为 .
S扇形= ????
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
