5.4一次函数的图象 (1)

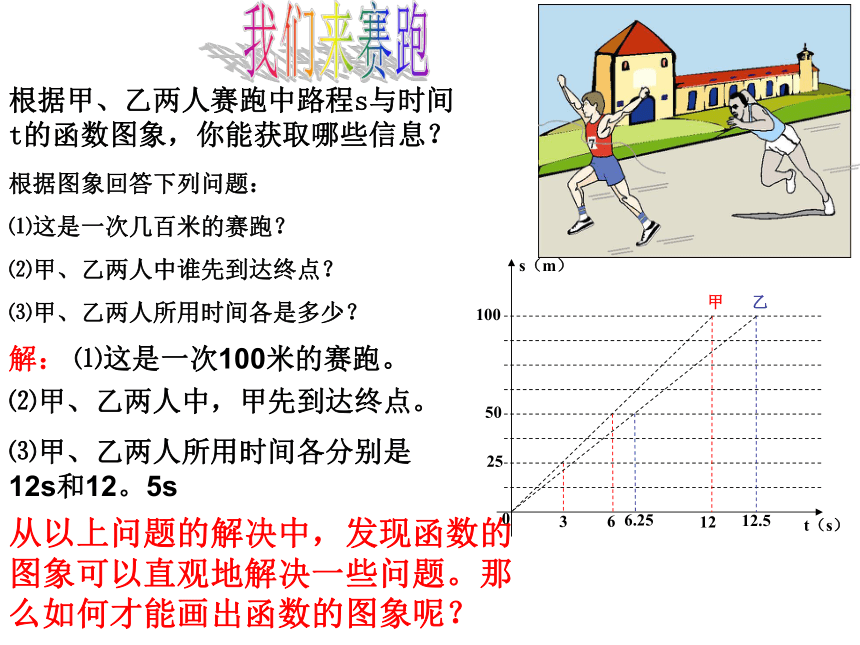
课件29张PPT。根据甲、乙两人赛跑中路程s与时间t的函数图象，你能获取哪些信息？根据图象回答下列问题：
⑴这是一次几百米的赛跑？
⑵甲、乙两人中谁先到达终点？
⑶甲、乙两人所用时间各是多少？从以上问题的解决中，发现函数的图象可以直观地解决一些问题。那么如何才能画出函数的图象呢？解： ⑴这是一次100米的赛跑。⑵甲、乙两人中，甲先到达终点。⑶甲、乙两人所用时间各分别是
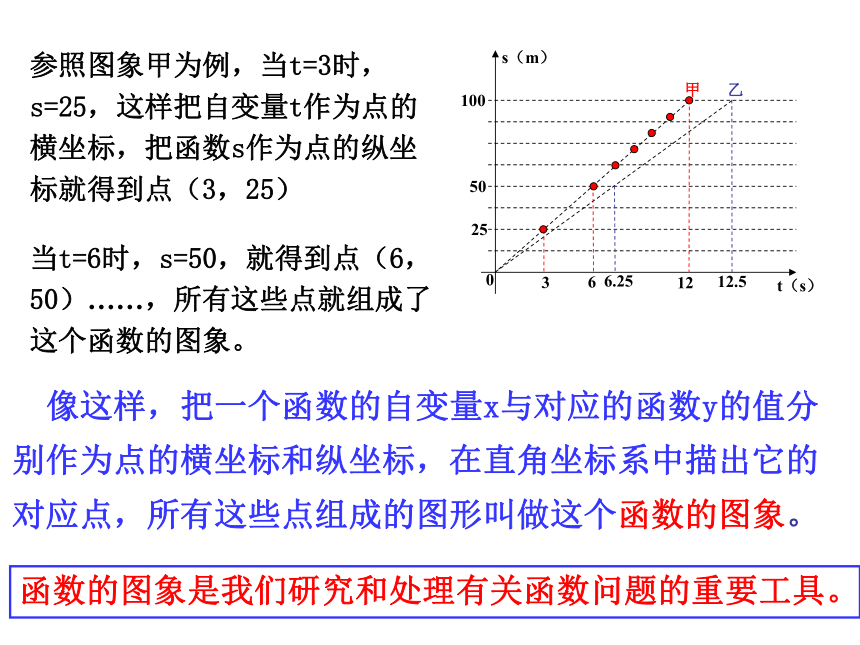
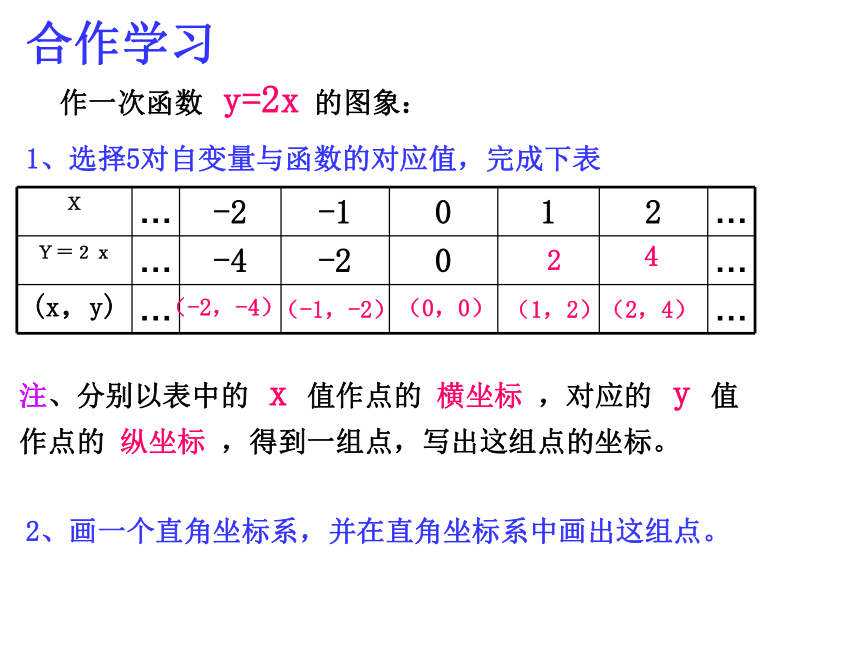
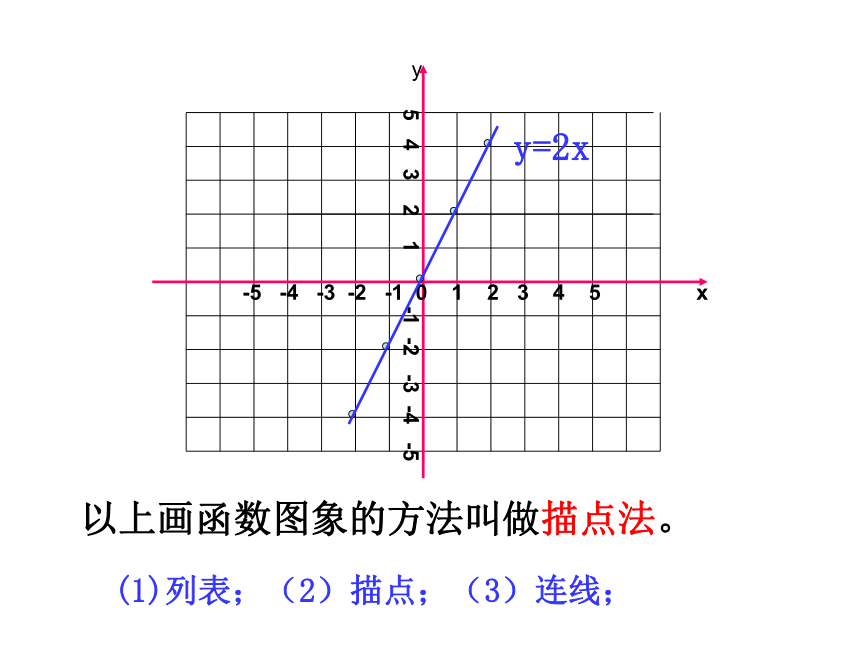
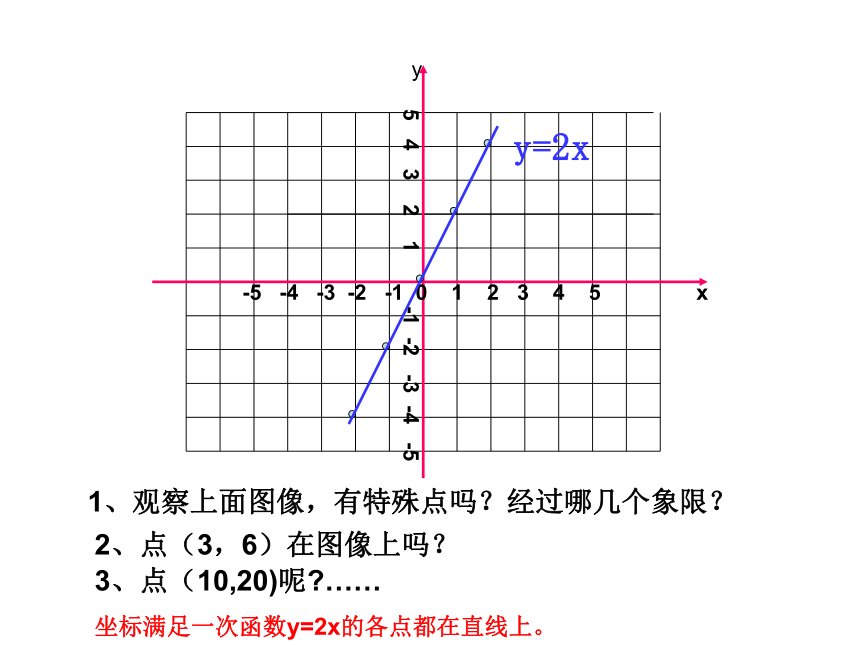
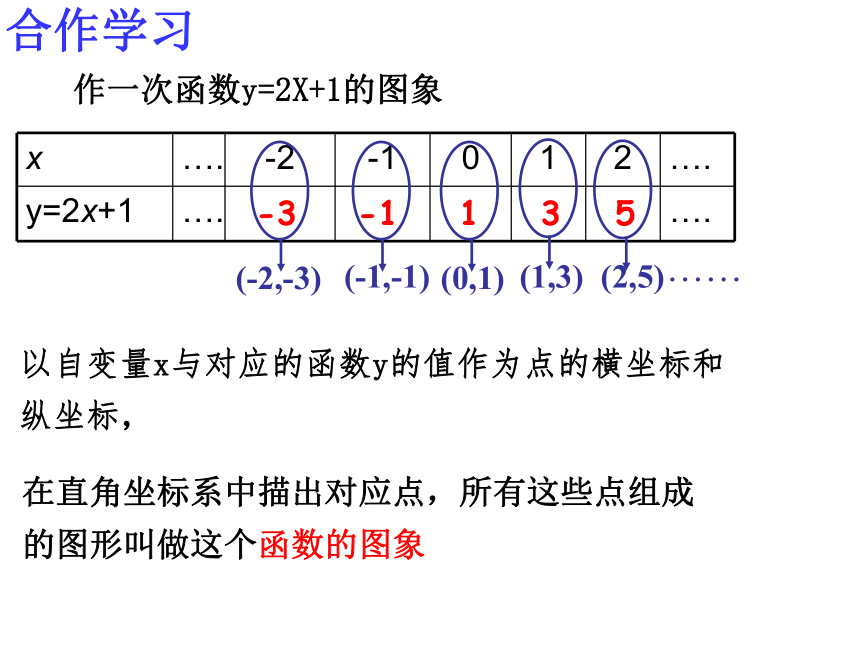
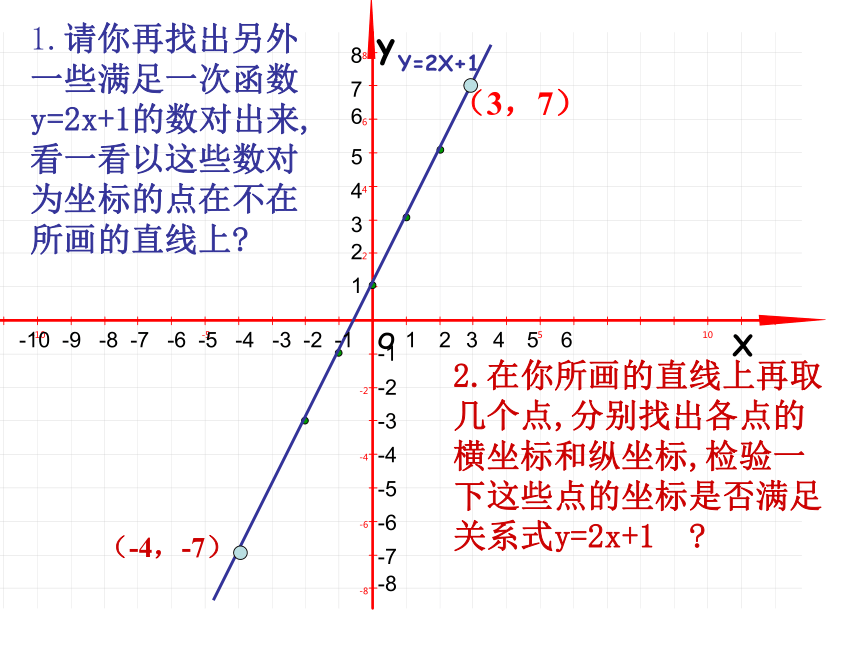
12s和12。5s参照图象甲为例，当t=3时，s=25，这样把自变量t作为点的横坐标，把函数s作为点的纵坐标就得到点（3，25）当t=6时，s=50，就得到点（6，50）……，所有这些点就组成了这个函数的图象。 像这样，把一个函数的自变量x与对应的函数y的值分别作为点的横坐标和纵坐标，在直角坐标系中描出它的对应点，所有这些点组成的图形叫做这个函数的图象。函数的图象是我们研究和处理有关函数问题的重要工具。泰顺六中 翁怀新2013年12月9日§5.4一次函数的图象（1）合作学习作一次函数 y=2x 的图象：注、分别以表中的 x 值作点的 横坐标 ，对应的 y 值作点的 纵坐标 ，得到一组点，写出这组点的坐标。2、画一个直角坐标系，并在直角坐标系中画出这组点。24（-1，-2）（0，0）（1，2）（2，4）（-2，-4）1、选择5对自变量与函数的对应值，完成下表-5 -4 -3 -2 -1 0 1 2 3 4 5 x 5 4 3 2 1 -1 -2 -3 -4 -5yy=2x以上画函数图象的方法叫做描点法。(1)列表；（2）描点；（3）连线；-5 -4 -3 -2 -1 0 1 2 3 4 5 x 5 4 3 2 1 -1 -2 -3 -4 -5yy=2x1、观察上面图像，有特殊点吗？经过哪几个象限？2、点（3，6）在图像上吗？3、点（10,20)呢?……坐标满足一次函数y=2x的各点都在直线上。-3-1135作一次函数y=2X+1的图象以自变量x与对应的函数y的值作为点的横坐标和纵坐标，……在直角坐标系中描出对应点，所有这些点组成的图形叫做这个函数的图象合作学习yXOY=2X+1 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1-1-2-3-4-5-612345612345678-7-8Y=2XyXOY=2X+1 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1-1-2-3-4-5-612345612345678-7-81.请你再找出另外一些满足一次函数y=2x+1的数对出来,看一看以这些数对为坐标的点在不在所画的直线上?2.在你所画的直线上再取几个点,分别找出各点的横坐标和纵坐标,检验一下这些点的坐标是否满足关系式y=2x+1 ?（3，7）（-4，-7）（1）根据上表，在直角坐标系已画出一次函数y=2x和Y=2X+1的图象，如右下图所示，观察所画的两组点,
(-2,-4),(-1,-2),(0,0),(1,2),(2,4);
(-2,-3),(-1,-1),(0,1),(1,3),(2,5);
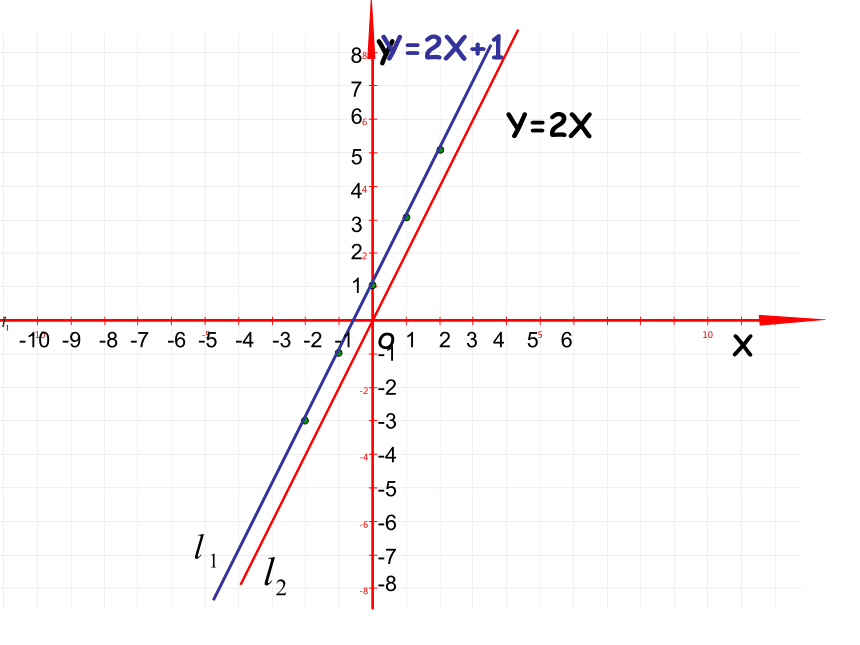
把你发现与同伴交流。xy012345-1-2-3-4-512345-1-2-3-4-5y-=2xY=2x+1所画的两组点，分别在两条不同的直线上.（1）如右图，坐标满足一次函数y=2x的各点(-2, -4), ( -1, -2 ), ( 0, 0), ( 1,2) , ( 2, 4 )……都在直线上 l1上吗？坐标满足y=2x+1的各点(-2,-3),(-1,-1 ),( 0,1),( 1,3 ),( 2,5 )……都在直线上 l2上吗？xy012345-1-2-3-4-512345-1-2-3-4-5反过来，在直线l1上取一些点，这些点的坐标都分别满足y=2x吗？在直线l2上取一些点，这些点的坐标都分别满足y=2x+1吗？Y=2x+1y-=2xYXOY=2XY=2X+1由此可见，一次函数Y=kx+b(k≠0,b为常数）可以用直角坐标系中的一条直线来表示, 从而这条直线就叫做一次函数Y=kx+b的图象. -10 -9 -8 -7 -6 -5 -4 -3 -2 -1-1-2-3-4-5-612345612345678-7-8一次函数y=kx+b(k≠0)的图象也叫做直线y=kx+b所以例1、在同一坐标系作出下列函数的图象，并求它们与坐标轴的交点坐标： y=3x, y=-3x+2思考：是不是画一次函数的图象都要用以上的描点法呢？有没有更简单、更快速的画法呢？分析：因为一次函数的图象是一条直线，根据两点确定一条直线，只要画出图象上的两个点就可以画出函数的图象。解：对于函数y=3x，
取x=0,得y=0，得到点（０，０）；取x=１,得y=３,得到点（１，３）对于函数y＝－3x+２，
取x=0，得y=2，得到点（0，2）；
取x=1,得y=－1,得到点（1，－1）过点（0，0），（1，3）画直线，就得到了函数y=3x的图象，其图象与坐标轴的交点是原点（0，0）y=3xy=－3x+2例1、在同一坐标系作出下列函数的图象，并求它们与坐标轴的交点坐标： y=3x, y=-3x+2两点法过点（0，2),(1，-1）画直线，就得到了函数y=-3x+2的图象，
其图象与x轴的交点是（ ，0），与y轴交点是（0，2）能否直接利用解析式求它们与坐标轴的交点坐标？当x=0时，y=？；当y=0时，x=？在函数y=3x中
当x=0时，y=0；当y=0时，x=0
∴与两坐标轴的交点坐标是（0，0）想一想在函数y=-3x+2中共同归纳 一次函数y=kx+b（k，b都为常数，k≠0），
当x=0时，y=b。函数图象与y轴的交点是（0，b）。正比例函数y=kx（k≠0）的图象必定经过原点（0，0）1.下列各点中，哪些点在函数y=4x+1的图象上?哪些点不在函数y=4x+1的图象上?为什么？
(2, 9) (5, 1) (-1, -3) (-0.5, -1)2练一练：3.若函数y=2x-3 的图象经过点(1,a) ,(b, 2)两点, 则a= ，b= ； -12.54.点已知M(-3, 4)在一次函数y=ax+1的图象上,则a的值是 ；-15、下列各点中，在直线y=2x－3上的是（ ）
（A）（0，3） （B）（1，1）
（C）（2，1） （D）（ －1，5）C6、1）若点（a，3）在直线y=2x－5上，则a=___（2）若点（2，－3）在直线y=kx+7上，则k=______4-5练一练：画一画（0≤x≤4）画函数图象时应注意：需考虑自变量的取值范围。
2、在如图，在Rt△ABC中，∠C=90°，AC=6，BC=8，P为BC边上一点（不与B、C重合）,设CP=x， △APB的面积为s。
（1）求s关于x的函数解析式及自变量x的取值范围。（2）画出函数的图象。小结通过这堂课的学习，你知道了什么？1、函数图象的画法：描点法4、满足一次函数的解析式的点都在图象上，图象上的每一个点的横坐标 x ，纵坐标 y 都满足一次函数解析式。(列表、描点、连线）
2、作函数图象的一般步骤：　由此结论可知画一次函数图象的方法可用两点法——一般取满足函数解析式的较方便的两个点，再连成直线即可。7、函数的代数表达式与函数图象是紧密联系着的，“数”用“形”表示，由“形”想到“数”，这是我们数学学习中一个很重要的思想方法——数形结合。 一次函数y=kx+b（k≠0）的图象是一条直线 。
所以一次函数y=kx+b的图象也叫做直线y=kx+b。5、一次函数的图象特征和画法:6、画函数图象时还应特别注意：需考虑自变量的取值范围。练一练1、函数y=2x+3的图象是（ ）
（A）过点（0，3），（0，- 1.5）的直线。
（B）过点（0，-1.5），（1，5）的直线。
（C）过点（-1.5，0），（-1，1）的直线。
（D）过点（0，3），（-1.5，0）的直线。C2、已知函数y=-8x+16，求该函数图象与y轴的交点是（ ， ），与x轴的交点是（ ， ）；图象与坐标轴围成的三角形面积是（ ）016203、已知一次函数的图象与坐标轴交与点（0，1），（1，0），求这个一次函数的解析式是 （ ） y=-x+1164、已知一次函数y=-2x+6。（1）求该函数的图象与坐标轴交点的坐标。（2）画出该函数的图象。5、一次函数y=2x-5的如象如图所示，你能求出直线y=2x-5与坐标轴的交点坐标吗？（2.5，0）（0，-5）同时你能求出直线y=2x-5与
坐标轴的交点坐标所围
成的三角形的面积？拓展提高1、已知直角坐标系中三点A（1，1），B（-1，3），C（3，-1）。这三点在同一直线上吗？请说明理由。 2、在同一条道路上，甲每时走3km，出发0.15时后，乙以每时4.5km的速度追甲。设乙行走的时间为t时。
（1）写出甲、乙两人所走的路程s与时间t的关系式；
（2）在同一直角坐标系中画出它们的图象；
（3）求出两条直线的交点坐标，并说明它的实际意义。解（1）S甲=3（0.15+ t ），
即 S甲=0.45+3t
S乙=4.5t 0 0.2 0.4 0.6 0.8 1.0 t4321拓展提高（3）两条直线的交点坐标（0.3,1.35),它的实际意义是乙出发0.3h后，在1.35km处追上甲.再见