专题：相似三角形的常见模型（含答案）

中小学教育资源及组卷应用平台
专题 相似三角形的常见模型
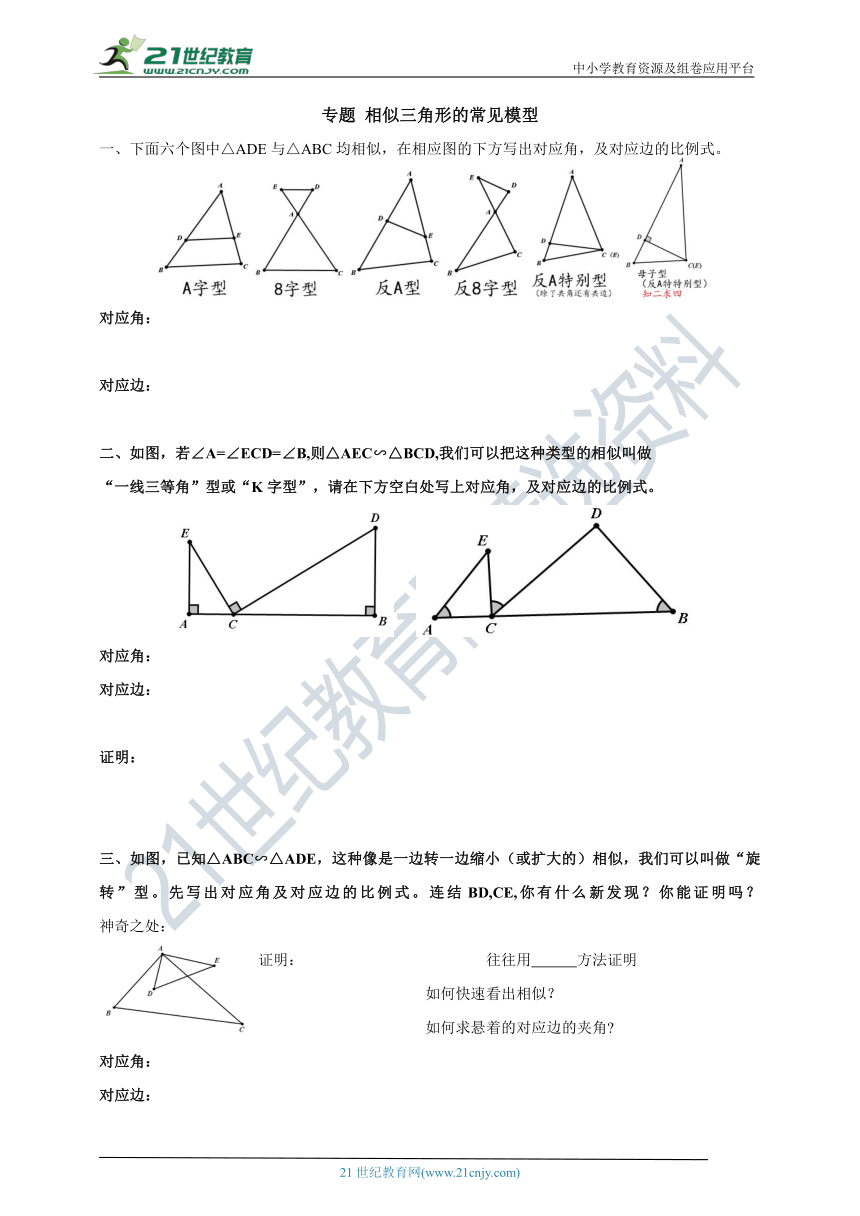
一、下面六个图中△ADE与△ABC均相似，在相应图的下方写出对应角，及对应边的比例式。
对应角：
对应边：
如图，若∠A=∠ECD=∠B,则△AEC∽△BCD,我们可以把这种类型的相似叫做
“一线三等角”型或“K字型”，请在下方空白处写上对应角，及对应边的比例式。
对应角：
对应边：
证明：
三、如图，已知△ABC∽△ADE，这种像是一边转一边缩小（或扩大的）相似，我们可以叫做“旋转”型。先写出对应角及对应边的比例式。连结BD,CE,你有什么新发现？你能证明吗？ 神奇之处：
证明： 往往用 方法证明
如何快速看出相似？
如何求悬着的对应边的夹角
对应角：
对应边：
练习:
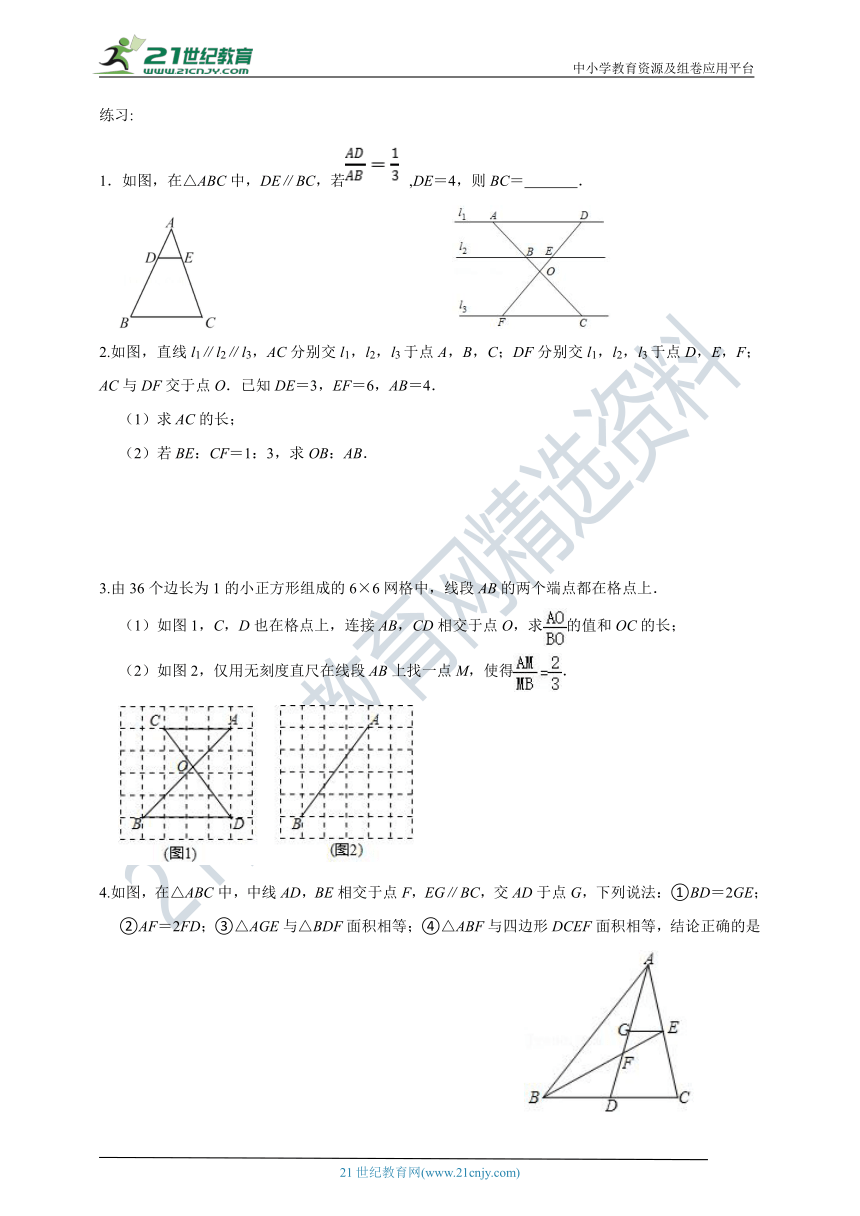
1．如图，在△ABC中，DE∥BC，若 ,DE＝4，则BC＝　 　．
2.如图，直线l1∥l2∥l3，AC分别交l1，l2，l3于点A，B，C；DF分别交l1，l2，l3于点D，E，F；AC与DF交于点O．已知DE＝3，EF＝6，AB＝4．
（1）求AC的长；
（2）若BE：CF＝1：3，求OB：AB．
3.由36个边长为1的小正方形组成的6×6网格中，线段AB的两个端点都在格点上．
（1）如图1，C，D也在格点上，连接AB，CD相交于点O，求的值和OC的长；
（2）如图2，仅用无刻度直尺在线段AB上找一点M，使得．
4.如图，在△ABC中，中线AD，BE相交于点F，EG∥BC，交AD于点G，下列说法：①BD＝2GE；②AF＝2FD；③△AGE与△BDF面积相等；④△ABF与四边形DCEF面积相等，结论正确的是
5.如图，图中相似三角形不一定成立的是（ ）
A.△CFD∽△AFB B.△CFA∽△DFB
C.△EAD∽△ECB D.△CAD∽△ACB
6.如图，已知△ABC中，AB＝，AC＝，BC＝6，点M为AB的中点，在线段AC上取点N，使△AMN与△ABC相似，求MN的长．
7.如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB于D．
（1）请写出图中所有的相似三角形：
（2）若AD＝2，DB＝8，则AC= ，BC= ，CD= ；
（3）若AC＝6，DB＝9，求AD= ，CD= ，BC= .
8.如图，点A，B，C，D为⊙O上的四个点，AC平分∠BAD，AC
交BD于点E，CE＝4，CD＝6，则AE的长为　 　．
9.(1)如图1，在△ABC中，D为AB上一点，∠ACD＝∠B．求证：AC2＝AD AB．
(2)如图2，在ABCD中，E为BC上一点，F为CD延长线上一点，∠BFE＝∠A．若BF＝4，BE＝3，求AD的长．
10.如图在平面直角坐标系xOy中，O为坐标原点，点A的坐标为（﹣1，2），点B在第一象限，且OB⊥OA，OB＝2OA，则B点的坐标为 ．
11.如图，已知△ABC和△ADE均为等边三角形，D在BC上，DE与AC相交于点F，AB＝8，BD＝2，则CF等于　 　．
12.△ABC和△ADE均是等腰直角三角形，其中∠ACB＝∠AED＝90°．如图1．开始时，DE∥AC，现在固定△ABC将△ADE绕着点A按顺时针方向旋转α（0＜α＜180°）；
（1）当△ADE中的DE边旋转到与△ABC的某条边平行时，旋转角α的度数是　 　；
（2）如图2，连接BD，CE，交于点P,求证：①△ABD∽△ACE；②∠BPC=45°
（3）若AB＝2AD，在△ADE的旋转过程中，当C，D，E三点在同一条直线上时，请画出图形．求∠DBC的度数．
略
略
练习：
12
2.（1）AC＝12；（2）．
3.（1）的值为，OC的长为；
（2）如图，点M即为所求作的点．
4. ①②④
5. D
6.MN的长为3或．
7.(1)相似的三角形有：△ACD和△ABC，△ACD和△CDB，△CDB和△ABC；
（2）CD＝4，AC＝2，BC＝4；
（3）AD＝3,CD＝3，BC＝6；
8. 5
9.（1）证明：∵∠ACD＝∠B，∠A＝∠A，
∴△ADC∽△ACB．∴＝．∴AC2＝AD AB．
（2）AD＝．
10. B（4，2）
11. 1.5
12.
（1）45°，90°
（2）∵△ABC和△ADE均是等腰直角三角形，其中∠ACB＝∠AED＝90°．
∴＝＝，∠BAC＝∠DAE＝45°，
∴∠BAC+∠DAC＝∠DAE+∠DAC，即∠BAD＝∠CAE，
∴△ABD∽△ACE；
（3）∠DBC为15°或75°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)