第五章 一次函数 章末复习------让函数的图像“说话” 课件(共11张PPT)
文档属性
| 名称 | 第五章 一次函数 章末复习------让函数的图像“说话” 课件(共11张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 246.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-20 22:29:13 | ||
图片预览


文档简介
(共11张PPT)
浙教版八上数学
第五章 一次函数 章末复习
让函数的图像“说话”
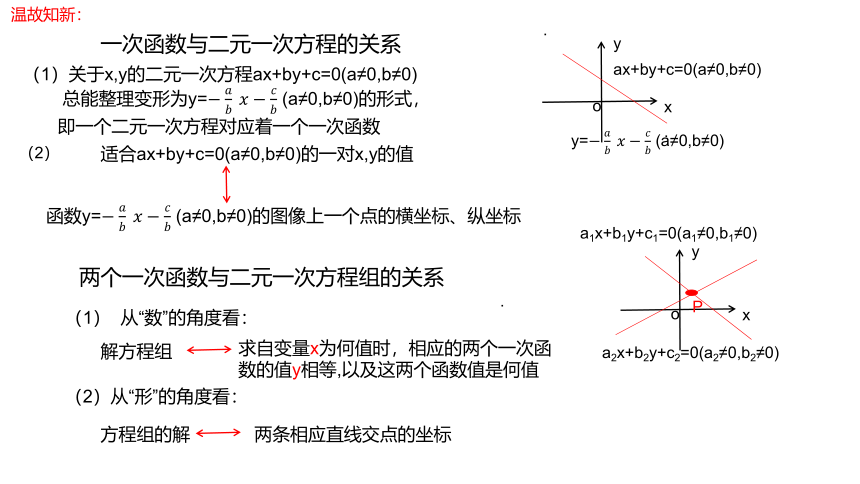
适合ax+by+c=0(a≠0,b≠0)的一对x,y的值
(2)
两个一次函数与二元一次方程组的关系
一次函数与二元一次方程的关系
(1) 从“数”的角度看:
(2)从“形”的角度看:
解方程组
求自变量x为何值时,相应的两个一次函数的值y相等,以及这两个函数值是何值
方程组的解
两条相应直线交点的坐标
温故知新:
x
y
o
ax+by+c=0(a≠0,b≠0)
y= (a≠0,b≠0)
.
函数y= (a≠0,b≠0)的图像上一个点的横坐标、纵坐标
.
x
y
o
a1x+b1y+c1=0(a1≠0,b1≠0)
a2x+b2y+c2=0(a2≠0,b2≠0)
P
(1)关于x,y的二元一次方程ax+by+c=0(a≠0,b≠0)
总能整理变形为y= (a≠0,b≠0)的形式,
即一个二元一次方程对应着一个一次函数
.
函数的图像会“说话”
1.在给定的函数中,把自变量 x 的一个值作为横坐标,对应的函数值 y 作为纵坐标,
在直角坐标系中描出相应的点,所有这些点的集合,叫做这个函数的图像.
函数图像直观、形象地表示两个变量之间的关系,实现了数形结合。
2.上升线表示因变量y随自变量x的增大而增大,
下降线表示因变量y随自变量x的增大而减小,
与x轴平行的直线表示因变量y没有随自变量x的变化而变化
3.运用运用函数的图象解题,关键要读懂函数图象的意义。
(1)与x轴平行的线段表示因变量y没有随自变量x的变化而变化------对应自变量x的取值范围
(2)要确定一次函数图象对应的表达式,只需知道函数图象上两个点的坐标即可。
(3)求两个函数图象的交点坐标,把这两个函数的表达式联立,建立方程组求解即可
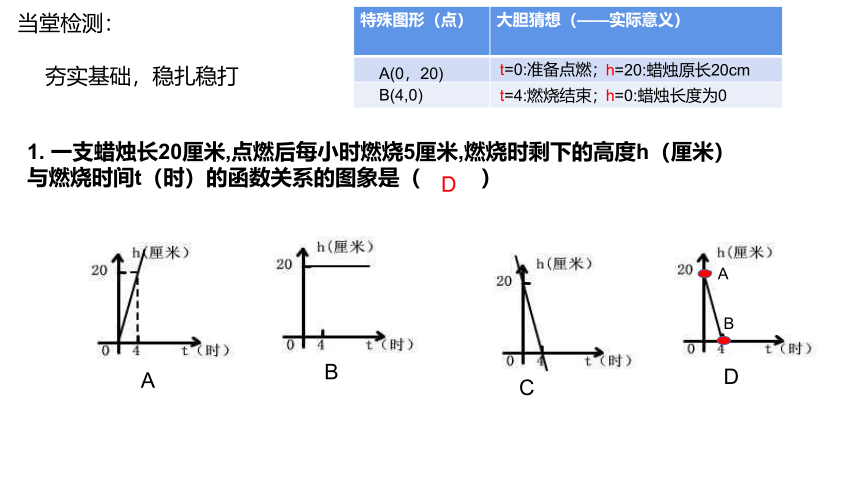
1. 一支蜡烛长20厘米,点燃后每小时燃烧5厘米,燃烧时剩下的高度h(厘米) 与燃烧时间t(时)的函数关系的图象是( )
A
C
B
D
A
B
D
特殊图形(点) 大胆猜想(——实际意义)
A(0,20)
t=0:准备点燃;
h=20:蜡烛原长20cm
B(4,0)
t=4:燃烧结束;
h=0:蜡烛长度为0
当堂检测:
夯实基础,稳扎稳打
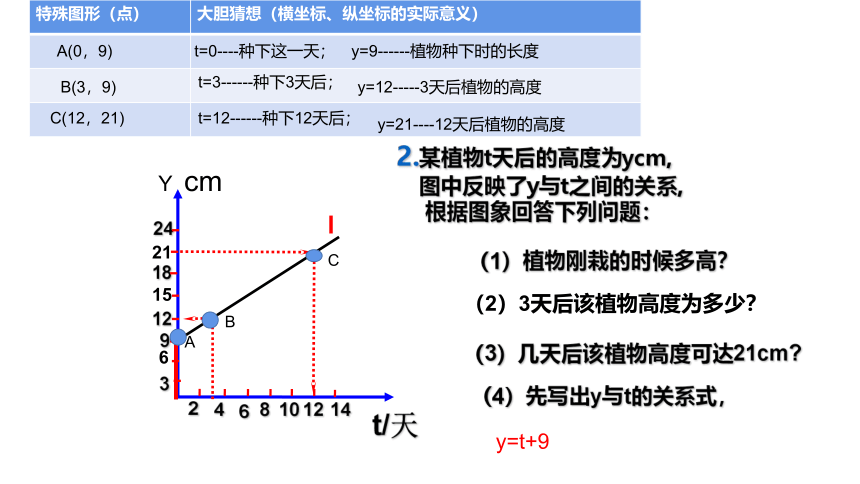
2.某植物t天后的高度为ycm,
图中反映了y与t之间的关系,
根据图象回答下列问题:
(1)植物刚栽的时候多高?
9
6
3
12
15
18
21
24
l
2
4
6
8
10
12
14
t/天
Y cm
(2)3天后该植物高度为多少?
(3)几天后该植物高度可达21cm
(4)先写出y与t的关系式,
A
B
C
特殊图形(点) 大胆猜想(横坐标、纵坐标的实际意义)
A(0,9)
t=0----种下这一天;
y=9------植物种下时的长度
B(3,9)
t=3------种下3天后;
y=12-----3天后植物的高度
C(12,21)
t=12------种下12天后;
y=21----12天后植物的高度
y=t+9
3. 近几年来,由于经济和社会发展迅速,用电矛盾越来越突出。为缓解用电紧张,某电力公司特制定了新的用电收费标准,每月用电量x(度)与应付电费y(元)的关系如图所示。
⑴根据图像所描述的信息,求当0≤x≤50和x>50时, y与x的函数关系式。
⑵根据以上分析:当每月用电量不超过50度时,收费标准是_______;当每月用电量超过50度时,收费标准是:______________________________
Y=0.5x (0≤x≤50)
Y=0.9x-20 (x>50)
不超过50度部分按0.5元/度计算,超过部分按0.9元/度计 算。
0.5元/度;
50
100
25
75
70
0
50
25
75
A
B
C
特殊图形(点)
大胆猜想(横坐标的实际意义,纵坐标的实际意义)
折点B(50,25)
当0≤x≤50时,收费标准是0.5元/度;
当x>50时,超过部分按0.9元/度计 算
特殊图形(点)
大胆猜想(实际意义)
小心求解
连续递推,豁然开朗
4. 某地长途汽车客运公司规定旅客可随身携带一定质量的行李,如果超过规定,则需要购买行李票,行李票费用y元与行李质量的关系如图:
旅客最多可免费携带多少千克行李?
(2)超过30千克后,每千克需付多少元?
(1)想一想紫红色那段图象表示什么意思?
A
B
C
D
行李票费用y=0元时,自变量x的取值范围
y=0.2x-6
当y=0时,0.2x-6=0,x=30
0.2元/千克
特殊图形(折点) 大胆猜想(横坐标的实际意义, 纵坐标的实际意义)
折点B(0,30)
当0≤x≤30时,不收行李费,
当x>30时,超过部分按0.2元/千克计 算
5.一辆轿车从甲城驶往乙城,同时一辆卡车从乙城驶往甲城,两车沿相同路线匀速行驶,轿车到达乙城停留一段时间后,按原路原速返回甲城;卡车到达甲城比轿车返回甲城早0.5小时,轿车比卡车每小时多行驶60千米,两车到达甲城后均停止行驶.两车之间的路程y(千米)与轿车行驶时间t(小时)的函数图象如图所示.请结合图象提供的信息解答下列问题:(1)请直接写出甲城和乙城之间的路程,并求出轿车和卡车的速度;
(2)求轿车在乙城停留的时间,并直接写出点D的坐标;
(3) 请直接写出轿车从乙城返回甲城过程中离甲城的路程s(千米)与轿车行驶时间t(小时) 之间的函数关系式.(不要求写出自变量的取值范围)
t(小时)
y(千米)
o
180
A
B
C
D
E
F
1
思维拓展,更上一层
特殊图形(点)
大胆猜想(横坐标、纵坐标实际意义)
小心求解(画线段图)
轿车:(x+60)km/h
甲城
乙城
卡车:x km/h
A(0,180)
横坐标t=0: 准备出发 ;
纵坐标s=180:甲城和乙城之间的距离
S甲乙两城=180(km)
B(1,0)
横坐标t=1: 两车相遇 ;
纵坐标s=0:两车之间的距离
x+(x+60)=180 ,x=60,
C(1.5,90)
横坐标t=1.5: 轿车到达乙城
纵坐标s=90:两车之间的距离
乙城
轿车
卡车
甲城
D(t2,y2)
横坐标t=t2:
轿车 --准备返回;
E(3,y3)
横坐标t=3: 卡车到达甲城 ;
轿车 --返回途中;
F(3.5,0)
横坐标t=3.5: 轿车到达甲城 ;
180÷120=1.5(小时)
180÷60=3(小时)
轿车停留时间:3+0.5-2×1.5=0.5(小时)
t(小时)
y(千米)
o
180
A
B
C
D
E
F
1
两车相遇
5.一辆轿车从甲城驶往乙城,同时一辆卡车从乙城驶往甲城,两车沿相同路线匀速行驶,轿车到达乙城停留一段时间后,按原路原速返回甲城;卡车到达甲城比轿车返回甲城早0.5小时,轿车比卡车每小时多行驶60千米,两车到达甲城后均停止行驶.两车之间的路程y(千米)与轿车行驶时间t(小时)的函数图象如图所示.请结合图象提供的信息解答下列问题:
(1)请直接写出甲城和乙城之间的路程,并求出轿车和卡车的速度;
(2)求轿车在乙城停留的时间,并直接写出点D的坐标;
(3) 请直接写出轿车从乙城返回甲城过程中离甲城的路程s(千米)与轿车行驶时间t(小时)之间的函数关系式.(不要求写出自变量的取值范围)
解:(1)甲城和乙城之间的路程为180千米,
设卡车的速度为x千米/时,
则轿车的速度为(x+60)千米/时,
由B(1,0)得,x+(x+60)=180 解得x=60,
∴x+60=120,
∴轿车和卡车的速度分别为120千米/时和60千米/时
(2)卡车到达甲城需180÷60=3(小时),
轿车从甲城到乙城需180÷120=1.5(小时),
3+0.5-1.5×2=0.5(小时),
∴轿车在乙城停留了0.5小时,点D的坐标为(2,120)
(3)s=180-120×(t-1.5-0.5)=-120t+420
特殊形(点)
大胆猜想(实际意义)
小心求解(情境模拟)
t(小时)
y(千米)
o
180
A
B
C
D
E
F
1
6.某公司快递员甲匀速骑车前往某小区送物件,出发几分钟后,快递员乙发现甲的手机落在公司,无法联系,于是乙匀速骑车去追赶甲.乙刚出发2分钟时,甲也发现自己手机落在公司,立刻按原路原速骑车回公司,2分钟后甲遇到乙,乙把手机给甲后立即原路原速返回公司,甲继续原路原速赶往某小区送物件,甲乙两人相距的路程y(米)与甲出发的时间x(分钟)之间的关系如图所示(乙给甲手机的时间忽略不计).则乙回到公司时,甲距公司的路程是 米.
解:由题意可得,
甲的速度为:4000÷(12﹣2﹣2)=500米/分,
乙的速度为:
=1000米/分
乙从与甲相遇到返回公司用的时间为4分钟,
则乙回到公司时,甲距公司的路程是:
500×(12﹣2)﹣500×2+500×4=6000(米),
A
B
C
D
E
倒过来思考:
点C的横坐标:12-2=10
点B的横坐标:10-2=8
浙教版八上数学
第五章 一次函数 章末复习
让函数的图像“说话”
适合ax+by+c=0(a≠0,b≠0)的一对x,y的值
(2)
两个一次函数与二元一次方程组的关系
一次函数与二元一次方程的关系
(1) 从“数”的角度看:
(2)从“形”的角度看:
解方程组
求自变量x为何值时,相应的两个一次函数的值y相等,以及这两个函数值是何值
方程组的解
两条相应直线交点的坐标
温故知新:
x
y
o
ax+by+c=0(a≠0,b≠0)
y= (a≠0,b≠0)
.
函数y= (a≠0,b≠0)的图像上一个点的横坐标、纵坐标
.
x
y
o
a1x+b1y+c1=0(a1≠0,b1≠0)
a2x+b2y+c2=0(a2≠0,b2≠0)
P
(1)关于x,y的二元一次方程ax+by+c=0(a≠0,b≠0)
总能整理变形为y= (a≠0,b≠0)的形式,
即一个二元一次方程对应着一个一次函数
.
函数的图像会“说话”
1.在给定的函数中,把自变量 x 的一个值作为横坐标,对应的函数值 y 作为纵坐标,
在直角坐标系中描出相应的点,所有这些点的集合,叫做这个函数的图像.
函数图像直观、形象地表示两个变量之间的关系,实现了数形结合。
2.上升线表示因变量y随自变量x的增大而增大,
下降线表示因变量y随自变量x的增大而减小,
与x轴平行的直线表示因变量y没有随自变量x的变化而变化
3.运用运用函数的图象解题,关键要读懂函数图象的意义。
(1)与x轴平行的线段表示因变量y没有随自变量x的变化而变化------对应自变量x的取值范围
(2)要确定一次函数图象对应的表达式,只需知道函数图象上两个点的坐标即可。
(3)求两个函数图象的交点坐标,把这两个函数的表达式联立,建立方程组求解即可
1. 一支蜡烛长20厘米,点燃后每小时燃烧5厘米,燃烧时剩下的高度h(厘米) 与燃烧时间t(时)的函数关系的图象是( )
A
C
B
D
A
B
D
特殊图形(点) 大胆猜想(——实际意义)
A(0,20)
t=0:准备点燃;
h=20:蜡烛原长20cm
B(4,0)
t=4:燃烧结束;
h=0:蜡烛长度为0
当堂检测:
夯实基础,稳扎稳打
2.某植物t天后的高度为ycm,
图中反映了y与t之间的关系,
根据图象回答下列问题:
(1)植物刚栽的时候多高?
9
6
3
12
15
18
21
24
l
2
4
6
8
10
12
14
t/天
Y cm
(2)3天后该植物高度为多少?
(3)几天后该植物高度可达21cm
(4)先写出y与t的关系式,
A
B
C
特殊图形(点) 大胆猜想(横坐标、纵坐标的实际意义)
A(0,9)
t=0----种下这一天;
y=9------植物种下时的长度
B(3,9)
t=3------种下3天后;
y=12-----3天后植物的高度
C(12,21)
t=12------种下12天后;
y=21----12天后植物的高度
y=t+9
3. 近几年来,由于经济和社会发展迅速,用电矛盾越来越突出。为缓解用电紧张,某电力公司特制定了新的用电收费标准,每月用电量x(度)与应付电费y(元)的关系如图所示。
⑴根据图像所描述的信息,求当0≤x≤50和x>50时, y与x的函数关系式。
⑵根据以上分析:当每月用电量不超过50度时,收费标准是_______;当每月用电量超过50度时,收费标准是:______________________________
Y=0.5x (0≤x≤50)
Y=0.9x-20 (x>50)
不超过50度部分按0.5元/度计算,超过部分按0.9元/度计 算。
0.5元/度;
50
100
25
75
70
0
50
25
75
A
B
C
特殊图形(点)
大胆猜想(横坐标的实际意义,纵坐标的实际意义)
折点B(50,25)
当0≤x≤50时,收费标准是0.5元/度;
当x>50时,超过部分按0.9元/度计 算
特殊图形(点)
大胆猜想(实际意义)
小心求解
连续递推,豁然开朗
4. 某地长途汽车客运公司规定旅客可随身携带一定质量的行李,如果超过规定,则需要购买行李票,行李票费用y元与行李质量的关系如图:
旅客最多可免费携带多少千克行李?
(2)超过30千克后,每千克需付多少元?
(1)想一想紫红色那段图象表示什么意思?
A
B
C
D
行李票费用y=0元时,自变量x的取值范围
y=0.2x-6
当y=0时,0.2x-6=0,x=30
0.2元/千克
特殊图形(折点) 大胆猜想(横坐标的实际意义, 纵坐标的实际意义)
折点B(0,30)
当0≤x≤30时,不收行李费,
当x>30时,超过部分按0.2元/千克计 算
5.一辆轿车从甲城驶往乙城,同时一辆卡车从乙城驶往甲城,两车沿相同路线匀速行驶,轿车到达乙城停留一段时间后,按原路原速返回甲城;卡车到达甲城比轿车返回甲城早0.5小时,轿车比卡车每小时多行驶60千米,两车到达甲城后均停止行驶.两车之间的路程y(千米)与轿车行驶时间t(小时)的函数图象如图所示.请结合图象提供的信息解答下列问题:(1)请直接写出甲城和乙城之间的路程,并求出轿车和卡车的速度;
(2)求轿车在乙城停留的时间,并直接写出点D的坐标;
(3) 请直接写出轿车从乙城返回甲城过程中离甲城的路程s(千米)与轿车行驶时间t(小时) 之间的函数关系式.(不要求写出自变量的取值范围)
t(小时)
y(千米)
o
180
A
B
C
D
E
F
1
思维拓展,更上一层
特殊图形(点)
大胆猜想(横坐标、纵坐标实际意义)
小心求解(画线段图)
轿车:(x+60)km/h
甲城
乙城
卡车:x km/h
A(0,180)
横坐标t=0: 准备出发 ;
纵坐标s=180:甲城和乙城之间的距离
S甲乙两城=180(km)
B(1,0)
横坐标t=1: 两车相遇 ;
纵坐标s=0:两车之间的距离
x+(x+60)=180 ,x=60,
C(1.5,90)
横坐标t=1.5: 轿车到达乙城
纵坐标s=90:两车之间的距离
乙城
轿车
卡车
甲城
D(t2,y2)
横坐标t=t2:
轿车 --准备返回;
E(3,y3)
横坐标t=3: 卡车到达甲城 ;
轿车 --返回途中;
F(3.5,0)
横坐标t=3.5: 轿车到达甲城 ;
180÷120=1.5(小时)
180÷60=3(小时)
轿车停留时间:3+0.5-2×1.5=0.5(小时)
t(小时)
y(千米)
o
180
A
B
C
D
E
F
1
两车相遇
5.一辆轿车从甲城驶往乙城,同时一辆卡车从乙城驶往甲城,两车沿相同路线匀速行驶,轿车到达乙城停留一段时间后,按原路原速返回甲城;卡车到达甲城比轿车返回甲城早0.5小时,轿车比卡车每小时多行驶60千米,两车到达甲城后均停止行驶.两车之间的路程y(千米)与轿车行驶时间t(小时)的函数图象如图所示.请结合图象提供的信息解答下列问题:
(1)请直接写出甲城和乙城之间的路程,并求出轿车和卡车的速度;
(2)求轿车在乙城停留的时间,并直接写出点D的坐标;
(3) 请直接写出轿车从乙城返回甲城过程中离甲城的路程s(千米)与轿车行驶时间t(小时)之间的函数关系式.(不要求写出自变量的取值范围)
解:(1)甲城和乙城之间的路程为180千米,
设卡车的速度为x千米/时,
则轿车的速度为(x+60)千米/时,
由B(1,0)得,x+(x+60)=180 解得x=60,
∴x+60=120,
∴轿车和卡车的速度分别为120千米/时和60千米/时
(2)卡车到达甲城需180÷60=3(小时),
轿车从甲城到乙城需180÷120=1.5(小时),
3+0.5-1.5×2=0.5(小时),
∴轿车在乙城停留了0.5小时,点D的坐标为(2,120)
(3)s=180-120×(t-1.5-0.5)=-120t+420
特殊形(点)
大胆猜想(实际意义)
小心求解(情境模拟)
t(小时)
y(千米)
o
180
A
B
C
D
E
F
1
6.某公司快递员甲匀速骑车前往某小区送物件,出发几分钟后,快递员乙发现甲的手机落在公司,无法联系,于是乙匀速骑车去追赶甲.乙刚出发2分钟时,甲也发现自己手机落在公司,立刻按原路原速骑车回公司,2分钟后甲遇到乙,乙把手机给甲后立即原路原速返回公司,甲继续原路原速赶往某小区送物件,甲乙两人相距的路程y(米)与甲出发的时间x(分钟)之间的关系如图所示(乙给甲手机的时间忽略不计).则乙回到公司时,甲距公司的路程是 米.
解:由题意可得,
甲的速度为:4000÷(12﹣2﹣2)=500米/分,
乙的速度为:
=1000米/分
乙从与甲相遇到返回公司用的时间为4分钟,
则乙回到公司时,甲距公司的路程是:
500×(12﹣2)﹣500×2+500×4=6000(米),
A
B
C
D
E
倒过来思考:
点C的横坐标:12-2=10
点B的横坐标:10-2=8
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
