第五章 一次函数 章末复习------眼里有数,心中有形 课件(共19张PPT)
文档属性
| 名称 | 第五章 一次函数 章末复习------眼里有数,心中有形 课件(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 633.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-20 22:27:28 | ||
图片预览


文档简介
(共19张PPT)
浙教版八上数学
第五章 一次函数 章末复习
眼里有形-------心中有数
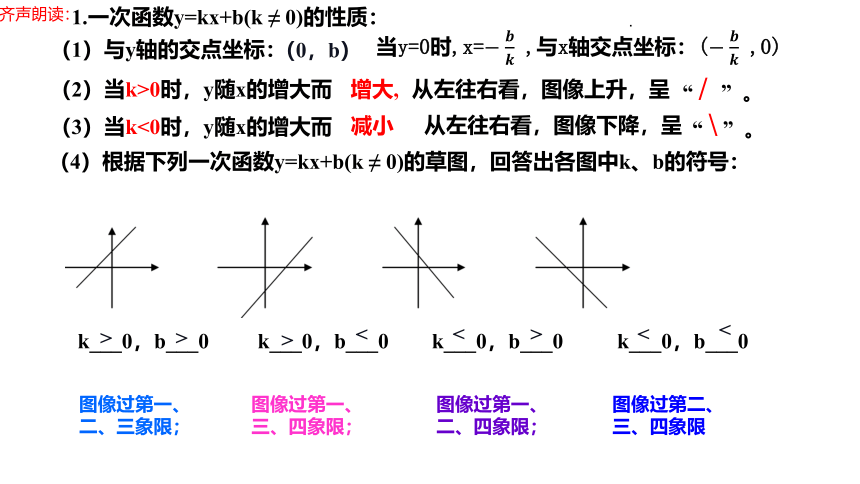
1.一次函数y=kx+b(k ≠ 0)的性质:
(1)与y轴的交点坐标:
(0,b)
(2)当k>0时,y随x的增大而
增大,
从左往右看,图像上升,呈
“ / ” 。
(3)当k<0时,y随x的增大而
减小
从左往右看,图像下降,呈
“ \ ” 。
(4)根据下列一次函数y=kx+b(k ≠ 0)的草图,回答出各图中k、b的符号:
k___0,b___0 k___0,b___0 k___0,b___0 k___0,b___0
>
>
>
<
<
>
<
<
图像过第一、
二、三象限;
图像过第一、
三、四象限;
图像过第一、
二、四象限;
图像过第二、三、四象限
齐声朗读:
当y=0时,x= ,与x轴交点坐标:( ,0)
.
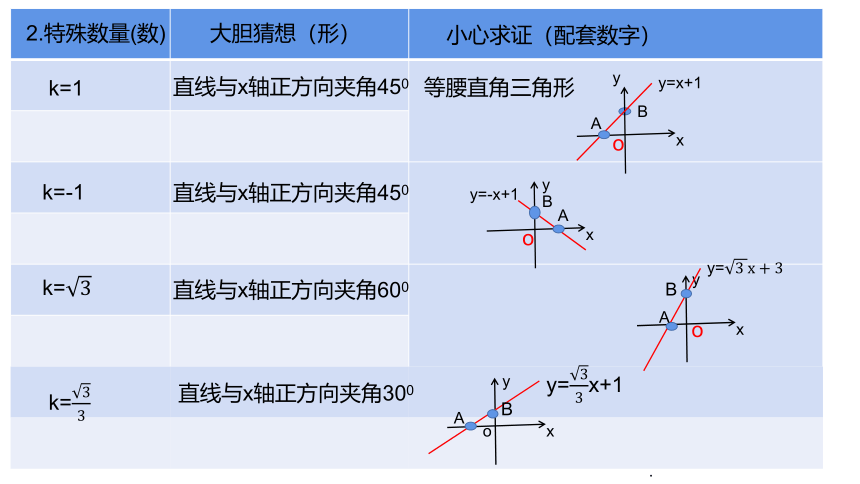
2.特殊数量(数)
大胆猜想(形)
小心求证(配套数字)
k=1
直线与x轴正方向夹角450
等腰直角三角形
B
x
y
o
A
y=x+1
x
y
o
A
y=-x+1
B
k=-1
直线与x轴正方向夹角450
k=
.
直线与x轴正方向夹角600
x
y
o
A
B
y=
k=
.
直线与x轴正方向夹角300
x
y
o
A
B
y=x+1
.
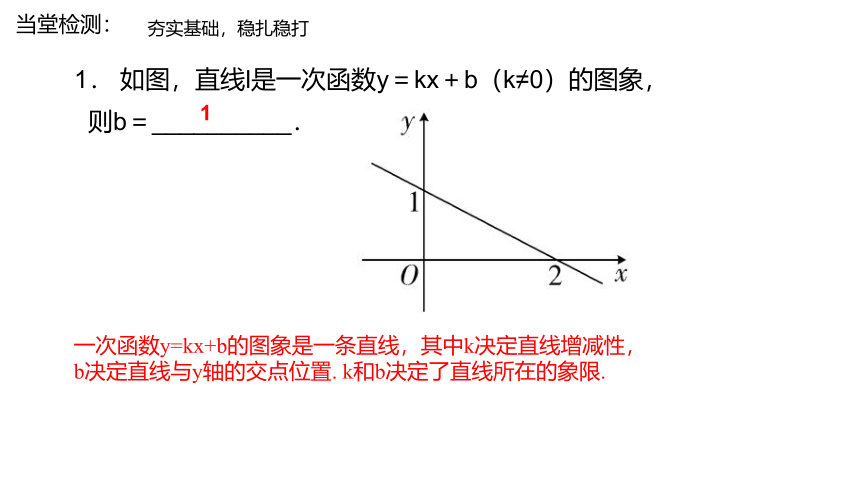
1. 如图,直线l是一次函数y=kx+b(k≠0)的图象,
则b=__________.
1
当堂检测:
夯实基础,稳扎稳打
一次函数y=kx+b的图象是一条直线,其中k决定直线增减性,
b决定直线与y轴的交点位置. k和b决定了直线所在的象限.
2 .已知一次函数 y =( m - 2 ) x -+ 1 .
.
( 1 ) m 为何值时,函数图象经过原点?
( 1 )∵函数图象经过原点,∴-+1=0 且 m - 2 ≠ 0 ,∴ m=-2
.
( 2 ) m 为何值时,函数图象经过( 0 ,- 3 )?
( 2 )将( 0 ,- 3 )代入解析式得,-+1=- 3,解得, m=±4 .
.
( 3 ) m 为何值时,函数图象平行于直线 y = 2 x ?
( 3 )∵函数图象平行于直线 y=2x ,∴ m-2=2 ,解得, m=4 .
( 4 ) m 为何值时,函数值 y 随 x 增大而减小?
( 4 ) ∵y 随 x 增大而减小,∴ m-2< 0 ,∴ m<2 .
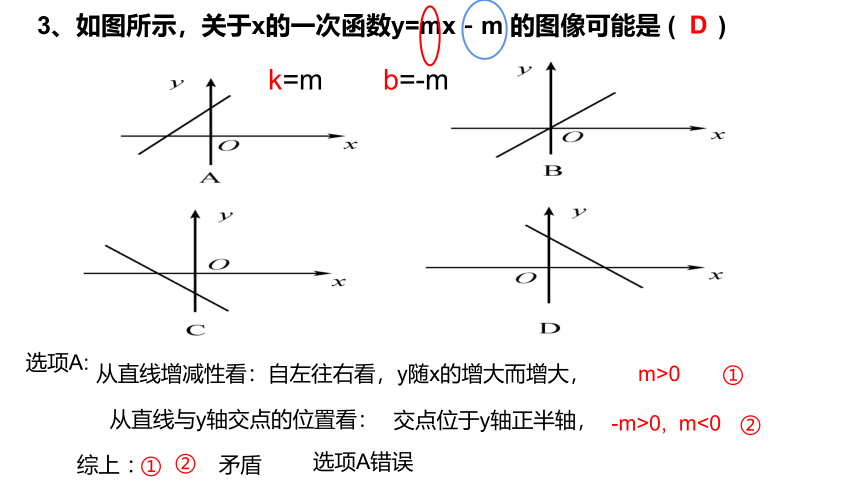
3、如图所示,关于x的一次函数y=mx-m 的图像可能是 ( )
D
k=m
b=-m
选项A:
从直线增减性看:
自左往右看,y随x的增大而增大,
m>0 ①
从直线与y轴交点的位置看:
交点位于y轴正半轴,
-m>0, m<0
②
②
①
综上 : 矛盾
选项A错误
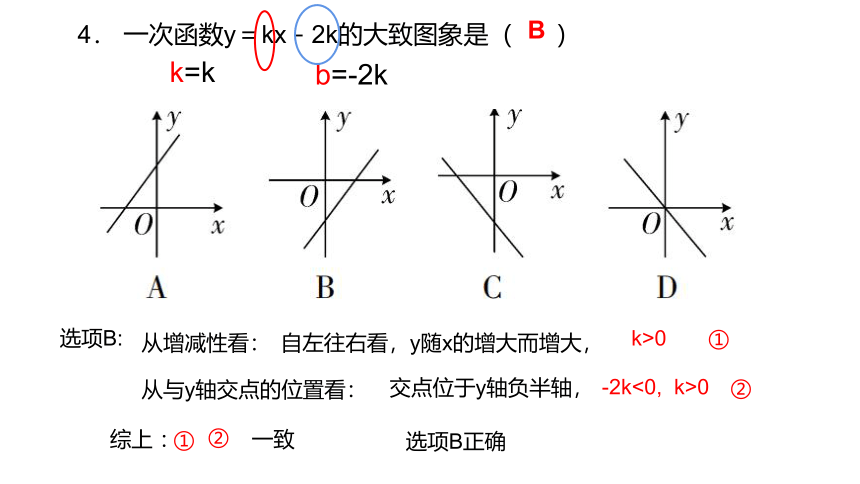
4. 一次函数y=kx-2k的大致图象是( )
B
选项B:
k=k
b=-2k
从增减性看:
自左往右看,y随x的增大而增大,
k>0 ①
从与y轴交点的位置看:
交点位于y轴负半轴,
-2k<0, k>0
②
②
①
综上 : 一致
选项B正确
5. 若一次函数y=kx+5在-1≤x≤4范围内有最大值17,求k的值。.
连续递推,豁然开朗
综上:k的值3或-12
注意到 b=5,是定值,
直线y=kx+5是一条过定点 (0,5)的直线
A
x
y
o
5
x
y
o
5
k不确定,分类讨论:
当k>0时,y随x的增大而增大,
-1
4
-1
4
17
当x=4时,y最大值=17
4k+5=17, k=3
当k<0时,y随x的增大而减小
当x= -1 时,y最大值=17
-k+5=17, k=12
B
y随x的增大而减小
∵ -2<-1,
∴
.
注意到:,k= <0
.
6. 已知,函数 的图象经过点M(-2 , ),点N(-1 , ) ,则 ( )
A. B. C. D. 无法确定
.
-2
-1
x
y
o
M
N
A
B
C
D
C
注意到:k相等-------
两直线平行,
.
直线与y轴交于正半轴
b决定直线与y轴的交点位置
7. 已知,函数 与在同一坐标系中的大致图象是 ( )
.
8. 如图,在同一坐标系中,关于x的一次函数
y = x+ b与 y = b x+1的图象只可能是( )
x
y
o
x
y
o
x
y
o
x
y
o
(A)
(B)
(C)
(D)
C
注意到:k=1-------
等腰直角三角形
眼中有数,心中有形
9.已知一次函数y=kx+b,y随着x的增大而减小,且kb<0,则在直角坐标系内它的大致图象是( )
(A) (B) (C) (D)
A
10.如图,一次函数y=kx+b的图象与正比例函数y=2x的图象平行且经过点A(1,﹣2),求k与b的值。
解:∵直线y=kx+b与直线y=2x平行
∴直线为y =2x - 4
∴k= 2
又直线过点A(1,-2)
∴-2=2×1+b
∴b= -4
11.若一次函数 y=kx+b 的图象经过第一、二、四象限,
则一次函数 y=bx-k 的图象是( )
由一次函数 y=kx+b 的图象经过第一、二、四象限,可知 k<0,b>0,因此一次函数 y=bx-k 中一次项系数大于 0,常数项大于 0,即一次函数 y=bx-k 的图象经过第一、二、三象限.故选 B.
B
12.一次函数 y=kx+b 与 y=kbx,它们在同一直角坐标系内的图象可能为( )
A项:从一次函数y=kx+b的图象看:k<0,b>0,∴kb<0,
从正比例函数y=kbx的图象看:kb<0,,两者一致,故A正确,
C项:从一次函数y=kx+b的图象看:k>0,b<0,∴kb<0,
从正比例函数y=kbx的图象看:kb>0, 两者矛盾,故C错误.
A
13.两直线的位置关系
若直线l1和l2的解析式为y=k1X+b1和y=k2X+b2,它们的位置关系可由其系数确定:
k1 ≠k2
<
>
l1和l2相交( l1和l2有且只有一个交点)
k1 =k2
<
>
l1和l2平行( l1和l2没有交点)
b1 ≠b2
k1 =k2
<
>
l1和l2重合
b1 =b2
13、如图,在平面直角坐标系中,直线L: 分别交两坐标轴于A、B两点,
M是线段AB上一个动点,设M的横坐标为x, △OMB的面积为S。
(1)写出S与x的函数关系式;
(2)若△OMB的面积为3,求点M的坐标;
(3)当△OMB是以OB为底的等腰三角形时,求它的面积.
思维拓展,更上一层
C
∴S△OMB=
解:(1)过点M做MC⊥OB于点C
∵点M在直线L上且横坐标为x, ∴MC=
∵点B为直线L与x轴的交点
∴B(4,0)
∴OB=4
(2)若△OMB的面积为3,求点M的坐标;
解:将S=3代入解析式
得:x=1
将x=1代入解析式
得:
∴点M的坐标为
(3)当△OMB是以OB为底的等腰三角形时,求它的面积.
∵△OMB是以OB为底的等腰三角形
∴OC=CB
C
解:过点M做MC⊥OB于点C
∴ M横坐标为2
将x=2代入解析式
得:y=1
即 MC=1
∴S△OMB=
浙教版八上数学
第五章 一次函数 章末复习
眼里有形-------心中有数
1.一次函数y=kx+b(k ≠ 0)的性质:
(1)与y轴的交点坐标:
(0,b)
(2)当k>0时,y随x的增大而
增大,
从左往右看,图像上升,呈
“ / ” 。
(3)当k<0时,y随x的增大而
减小
从左往右看,图像下降,呈
“ \ ” 。
(4)根据下列一次函数y=kx+b(k ≠ 0)的草图,回答出各图中k、b的符号:
k___0,b___0 k___0,b___0 k___0,b___0 k___0,b___0
>
>
>
<
<
>
<
<
图像过第一、
二、三象限;
图像过第一、
三、四象限;
图像过第一、
二、四象限;
图像过第二、三、四象限
齐声朗读:
当y=0时,x= ,与x轴交点坐标:( ,0)
.
2.特殊数量(数)
大胆猜想(形)
小心求证(配套数字)
k=1
直线与x轴正方向夹角450
等腰直角三角形
B
x
y
o
A
y=x+1
x
y
o
A
y=-x+1
B
k=-1
直线与x轴正方向夹角450
k=
.
直线与x轴正方向夹角600
x
y
o
A
B
y=
k=
.
直线与x轴正方向夹角300
x
y
o
A
B
y=x+1
.
1. 如图,直线l是一次函数y=kx+b(k≠0)的图象,
则b=__________.
1
当堂检测:
夯实基础,稳扎稳打
一次函数y=kx+b的图象是一条直线,其中k决定直线增减性,
b决定直线与y轴的交点位置. k和b决定了直线所在的象限.
2 .已知一次函数 y =( m - 2 ) x -+ 1 .
.
( 1 ) m 为何值时,函数图象经过原点?
( 1 )∵函数图象经过原点,∴-+1=0 且 m - 2 ≠ 0 ,∴ m=-2
.
( 2 ) m 为何值时,函数图象经过( 0 ,- 3 )?
( 2 )将( 0 ,- 3 )代入解析式得,-+1=- 3,解得, m=±4 .
.
( 3 ) m 为何值时,函数图象平行于直线 y = 2 x ?
( 3 )∵函数图象平行于直线 y=2x ,∴ m-2=2 ,解得, m=4 .
( 4 ) m 为何值时,函数值 y 随 x 增大而减小?
( 4 ) ∵y 随 x 增大而减小,∴ m-2< 0 ,∴ m<2 .
3、如图所示,关于x的一次函数y=mx-m 的图像可能是 ( )
D
k=m
b=-m
选项A:
从直线增减性看:
自左往右看,y随x的增大而增大,
m>0 ①
从直线与y轴交点的位置看:
交点位于y轴正半轴,
-m>0, m<0
②
②
①
综上 : 矛盾
选项A错误
4. 一次函数y=kx-2k的大致图象是( )
B
选项B:
k=k
b=-2k
从增减性看:
自左往右看,y随x的增大而增大,
k>0 ①
从与y轴交点的位置看:
交点位于y轴负半轴,
-2k<0, k>0
②
②
①
综上 : 一致
选项B正确
5. 若一次函数y=kx+5在-1≤x≤4范围内有最大值17,求k的值。.
连续递推,豁然开朗
综上:k的值3或-12
注意到 b=5,是定值,
直线y=kx+5是一条过定点 (0,5)的直线
A
x
y
o
5
x
y
o
5
k不确定,分类讨论:
当k>0时,y随x的增大而增大,
-1
4
-1
4
17
当x=4时,y最大值=17
4k+5=17, k=3
当k<0时,y随x的增大而减小
当x= -1 时,y最大值=17
-k+5=17, k=12
B
y随x的增大而减小
∵ -2<-1,
∴
.
注意到:,k= <0
.
6. 已知,函数 的图象经过点M(-2 , ),点N(-1 , ) ,则 ( )
A. B. C. D. 无法确定
.
-2
-1
x
y
o
M
N
A
B
C
D
C
注意到:k相等-------
两直线平行,
.
直线与y轴交于正半轴
b决定直线与y轴的交点位置
7. 已知,函数 与在同一坐标系中的大致图象是 ( )
.
8. 如图,在同一坐标系中,关于x的一次函数
y = x+ b与 y = b x+1的图象只可能是( )
x
y
o
x
y
o
x
y
o
x
y
o
(A)
(B)
(C)
(D)
C
注意到:k=1-------
等腰直角三角形
眼中有数,心中有形
9.已知一次函数y=kx+b,y随着x的增大而减小,且kb<0,则在直角坐标系内它的大致图象是( )
(A) (B) (C) (D)
A
10.如图,一次函数y=kx+b的图象与正比例函数y=2x的图象平行且经过点A(1,﹣2),求k与b的值。
解:∵直线y=kx+b与直线y=2x平行
∴直线为y =2x - 4
∴k= 2
又直线过点A(1,-2)
∴-2=2×1+b
∴b= -4
11.若一次函数 y=kx+b 的图象经过第一、二、四象限,
则一次函数 y=bx-k 的图象是( )
由一次函数 y=kx+b 的图象经过第一、二、四象限,可知 k<0,b>0,因此一次函数 y=bx-k 中一次项系数大于 0,常数项大于 0,即一次函数 y=bx-k 的图象经过第一、二、三象限.故选 B.
B
12.一次函数 y=kx+b 与 y=kbx,它们在同一直角坐标系内的图象可能为( )
A项:从一次函数y=kx+b的图象看:k<0,b>0,∴kb<0,
从正比例函数y=kbx的图象看:kb<0,,两者一致,故A正确,
C项:从一次函数y=kx+b的图象看:k>0,b<0,∴kb<0,
从正比例函数y=kbx的图象看:kb>0, 两者矛盾,故C错误.
A
13.两直线的位置关系
若直线l1和l2的解析式为y=k1X+b1和y=k2X+b2,它们的位置关系可由其系数确定:
k1 ≠k2
<
>
l1和l2相交( l1和l2有且只有一个交点)
k1 =k2
<
>
l1和l2平行( l1和l2没有交点)
b1 ≠b2
k1 =k2
<
>
l1和l2重合
b1 =b2
13、如图,在平面直角坐标系中,直线L: 分别交两坐标轴于A、B两点,
M是线段AB上一个动点,设M的横坐标为x, △OMB的面积为S。
(1)写出S与x的函数关系式;
(2)若△OMB的面积为3,求点M的坐标;
(3)当△OMB是以OB为底的等腰三角形时,求它的面积.
思维拓展,更上一层
C
∴S△OMB=
解:(1)过点M做MC⊥OB于点C
∵点M在直线L上且横坐标为x, ∴MC=
∵点B为直线L与x轴的交点
∴B(4,0)
∴OB=4
(2)若△OMB的面积为3,求点M的坐标;
解:将S=3代入解析式
得:x=1
将x=1代入解析式
得:
∴点M的坐标为
(3)当△OMB是以OB为底的等腰三角形时,求它的面积.
∵△OMB是以OB为底的等腰三角形
∴OC=CB
C
解:过点M做MC⊥OB于点C
∴ M横坐标为2
将x=2代入解析式
得:y=1
即 MC=1
∴S△OMB=
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
