初中数学浙教版九年级上册 专题训练:圆动点问题(含答案)
文档属性
| 名称 | 初中数学浙教版九年级上册 专题训练:圆动点问题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 435.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-20 18:03:29 | ||
图片预览




文档简介
登录二一教育在线组卷平台 助您教考全无忧
专题训练:圆动点问题
一、单选题
1.如图,在矩形中,,,为矩形内一点,,连接,则的最小值为( )
A.8 B. C.10 D.
2.在Rt△ABC中,∠C=90°,AC=10,BC=12,点D为线段BC上一动点.以CD为⊙O直径,作AD交⊙O于点E,连BE,则BE的最小值为( )
A.6 B.8 C.10 D.12
3.如图,AB是半圆O的直径,点C在半圆O上,OA=10,BC=16,D是弧AC上一个动点,连接BD,过点C作CM⊥BD,连接AM,在点D移动的过程中,AM的最小值为( )
A. B. C. D.
4.如图,正比例函数y=2x与反比例函数的图象交于A、B两点,点P在以为圆心,1为半径的⊙C上运动,点Q是AP的中点,则OQ长的最大值为( )
A.2 B. C. D.
5.已知的直径,与的弦垂直,垂足为,且,则直径上的点(包含端点)与点的距离为整数的点有( )
A.1个 B.3个 C.6个 D.7个
6.如图,在中,,点O是的三等分点,半圆O与相切,M,N分别是与半圆弧上的动点,则的最小值和最大值之和是( )
A.8 B.10 C.12 D.14
7.如图,点A的坐标是( 2,0),点C是以OA为直径的⊙B上的一动点,点A关于点C的对称点为点P. 当点C在⊙ B上运动时,所有这样的点P组成的图形与直线y=kx-3(k>0)有且只有一个公共点,则k的值是()
A. B. C. D.
8.如图,在平面直角坐标系中,直线 分别与x轴、y轴相交于点A、B,点E、F分别是正方形 的边 、 上的动点,且 ,过原点O作 ,垂足为H,连接 、 ,则 面积的最大值为()
A. B.12 C. D.
9.如图, 是 的直径, , 是半径 上的一动点, 交 于点 ,在半径 上取点 ,使得 , 交 于点 ,点 位于 两侧,连结 交 于点 .点 从点 出发沿 向终点 运动,在整个运动过程中, 与 的面积和的变化情况是( )
A.一直减小 B.一直不变
C.先变大后变小 D.先变小后变大
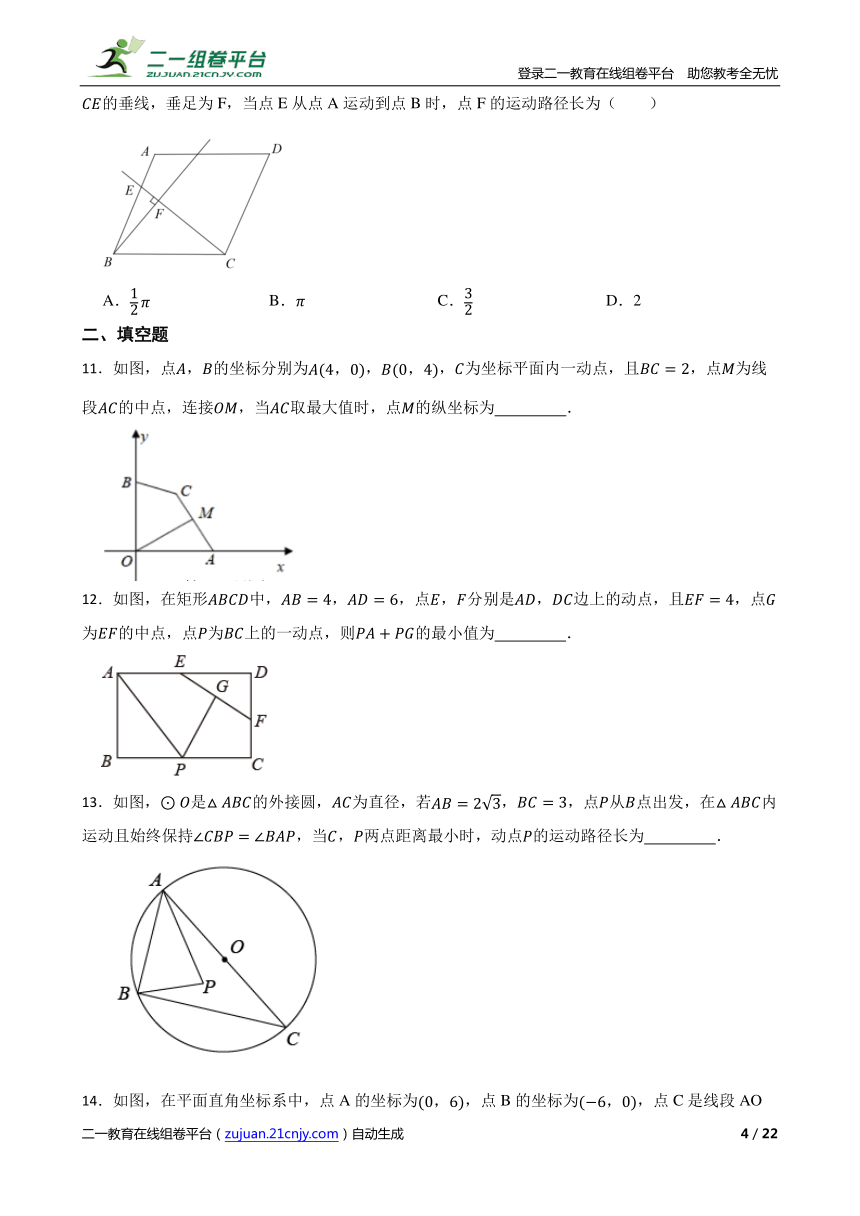
10.在平行四边形中,,,,点E是边上的动点,过点B作直线的垂线,垂足为F,当点E从点A运动到点B时,点F的运动路径长为( )
A. B. C. D.2
二、填空题
11.如图,点,的坐标分别为,,为坐标平面内一动点,且,点为线段的中点,连接,当取最大值时,点的纵坐标为 .
12.如图,在矩形中,,,点,分别是,边上的动点,且,点为的中点,点为上的一动点,则的最小值为 .
13.如图,是的外接圆,为直径,若,,点从点出发,在内运动且始终保持,当,两点距离最小时,动点的运动路径长为 .
14.如图,在平面直角坐标系中,点A的坐标为,点B的坐标为,点C是线段AO上的一个动点,连接BC,于点D,以OD为一边,作正方形ODEF,其中点E与点B在直线OD两侧,当点C从点A运动到点O过程中,点E经过的路径长为 .
15.如图,在中,,将绕点顺时针旋转90°得到,为线段上的动点,以为圆心、为半径作⊙,当⊙与的边相切时,⊙的半径的长为 .
16.如图,、,以为直径作,射线交于、两点,为弧的中点,为的中点.当射线绕点旋转时,的最小值为 .
17.如图,直线l与圆O相交于A、B两点,AC是圆O的弦,OC∥AB,半径OC的长为10,弦AB的长为12,动点P从点A出发以每秒1个单位的速度沿射线AB方向运动.当△APC是直角三角形时,动点P运动的时间t为 秒.
18.图,在⊙O中,AC,BD是直径,∠BOC=60°,点P是劣弧AB上任意一点(不与A、B重合),过点P作AC垂线,交AC、BD所在直线于点E,F,过点P作BD垂线,交BD、AC所在直线于点G、H,下列选项中,正确的是 .
①;②∠GPE=60°;③PG+PE最大值为;④当△PEH≌△CBA时,.
19.如图,在直角坐标系中,的圆心A的坐标为(1,0),半径为1,点P为直线上的动点,过点P作的切线,切点为Q,则切线长PQ的最小值是 .
20.如图,在矩形中,,,点E、F分别是边、上的动点,且,点G是的中点,、,则四边形面积的最小值为 .
三、解答题
21.如图,在直角坐标系中,直线 与 轴交于 点,与 轴交于 点,以 为直径作圆 ,过 作圆 的切线交 轴于点 .
(1)求 点的坐标;
(2)设点 为 延长线上一点, , 为线段 上的一个动点(异于 , ),过 点作 轴的平行线交 于 ,交 的延长线于 ,试判断 的值是否为定值,如果是,则求出这个值;如果不是,请说明理由.
22.在平面直角坐标系中,已知点A(2,0),点B(0, ).点O(0,0).△AOB绕着点O顺时针旋转,得到△A'OB',点A、B旋转后的对应点为A'、B',记旋转角为α.
(Ⅰ)如图1,若α=30°,求点B'的坐标;
(Ⅱ)如图2,若0°<α<90°,设直线AA'和直线BB'交于点P,求证:AA'⊥BB';
(Ⅲ)在(Ⅱ)中的条件下,若0°<α<360°,点C(﹣2,0).求线段CP长度的取值范围.(直接写出结果即可)
23.如图,在平面直角坐标系中,点A的坐标为(3,0),点B的坐标为(﹣3,0).过点B的直线绕点B逆时针方向旋转,过程中与y轴交于点C.过点A作AD⊥BC于点D,求在点C坐标由(0, )到(0,3 )的过程中点D运动的路径长.
24.对于平面内的⊙C和⊙C外一点Q,给出如下定义:若过点Q的直线与⊙C存在公共点,记为点A,B,设 ,则称点A(或点B)是⊙C的“K相关依附点”,特别地,当点A和点B重合时,规定AQ=BQ, (或 ).
已知在平面直角坐标系xOy中,Q(-1,0),C(1,0),⊙C的半径为r.
(1)如图1,当 时,
①若A1(0,1)是⊙C的“k相关依附点”,求k的值.
②A2(1+ ,0)是否为⊙C的“2相关依附点”.
(2)若⊙C上存在“k相关依附点”点M,
①当r=1,直线QM与⊙C相切时,求k的值.
②当 时,求r的取值范围.
(3)若存在r的值使得直线 与⊙C有公共点,且公共点时⊙C的“ 相关依附点”,直接写出b的取值范围.
四、综合题
25.在平面直角坐标系中,已知点对于点给出如下定义:将点向右或向左平移个单位长度,再向上或向下平移个单位长度,得到点,点关于点的对称点为,称点为点的“对应点”.
(1)如图,点点在线段的延长线上,若点点为点的“对应点”.
①在图中画出点;
②连接交线段于点求证:
(2)的半径为1,是上一点,点在线段上,且,若为外一点,点为点的“对应点”,连接当点在上运动时直接写出长的最大值与最小值的差(用含的式子表示)
26.如图,四边形ABCD中, ,∠ABC=90°,∠C=30°,AD=3, ,DH⊥BC于点H.将△PQM与该四边形按如图方式放在同一平面内,使点P与A重合,点B在PM上,其中∠Q=90°,∠QPM=30°, .
(1)求证:△PQM≌△CHD;
(2)△PQM从图1的位置出发,先沿着BC方向向右平移(图2),当点P到达点D后立刻绕点D逆时针旋转(图3),当边PM旋转50°时停止.
①边PQ从平移开始,到绕点D旋转结束,求边PQ扫过的面积;
②如图2,点K在BH上,且 .若△PQM右移的速度为每秒1个单位长,绕点D旋转的速度为每秒5°,求点K在△PQM区域(含边界)内的时长;
③如图3.在△PQM旋转过程中,设PQ,PM分别交BC于点E,F,若BE=d,直接写出CF的长(用含d的式子表示).
27.在△ ABC中,∠BAC=90° ,AB=AC= ,D为 BC的中点,E,F分别为AC, AD 上任意一点,连接EF,将线段EF绕点E顺时针旋转 90°得到线段EG,连接FG, AG.
(1)如图1,点 E 与点 C 重合,且 GF 的延长线过点 B ,若点 P 为 FG 的中点,连接 PD,求 PD的长;
(2)如图 2,EF 的延长线交 AB 于点M,点N在 AC上, ∠AGN=∠AEG 且GN=MF,求证:AM+AF= AE
(3)如图3,F为线段 AD上一动点,E为 AC的中点,连接BE,H为直线BC上一动点,连接 EH,将△ BEH沿EH翻折至△ABC所在平面内,得到△ B'EH',连接 B'G,直接写出线段 B'G的长度的最小值
28.在平面直角坐标系中,的半径为1,对于和直线给出如下定义:若的一条边关于直线的对称线段是的弦,则称是的关于直线的“关联三角形”,直线是“关联轴”.
(1)如图1,若是的关于直线的“关联三角形”,请画出与的“关联轴”(至少画两条);
(2)若中,点坐标为,点坐标为,点在直线的图像上,存在“关联轴”使是的关联三角形,求点横坐标的取值范围;
(3)已知,将点向上平移2个单位得到点,以为圆心为半径画圆,,为上的两点,且(点在点右侧),若与的关联轴至少有两条,直接写出的最小值和最大值,以及最大时的长.
答案解析部分
1.【答案】A
2.【答案】B
3.【答案】D
4.【答案】D
5.【答案】C
6.【答案】C
7.【答案】D
8.【答案】D
9.【答案】B
10.【答案】B
11.【答案】
12.【答案】8
13.【答案】
14.【答案】
15.【答案】或
16.【答案】
17.【答案】16或20
18.【答案】①②④
19.【答案】
20.【答案】38
21.【答案】(1)∵BC是圆的切线,
∴BC⊥AB,
∵直线AB的解析式为,
∴直线BC的解析式为y=2x+4,令y=0,
∴2x+4=0,∴x=-2,
∴C(-2,0);
(2)PM+PN的值是定值,定值为20。将x=0代入直线,得到y=4,
∴B(4,0),再将y=0代入直线,得到x=8,
∴A(8,0),由(1)可知:C(-2,0),∵CDBC,
∴D(-4,-4),∵A(8,0),
∴直线AD的解析式为,
∵点P再线段BC上,设P(m,2m+4)(-2∵PM//x轴,
∴M(-4m,2m+4),N(6m+20,2m+4),
∴PM+PN=-4m-m+(6m+20-m)=20,即:PM+PN的值是定值,定值为20.
22.【答案】解:(Ⅰ)如图1,设A'B'与x轴交于点H,
∵OA=2,OB=2 ,∠AOB=90°,
∴AB=4,
∴∠ABO=∠B'=30°,
∵∠BOB'=α=30°,
∴BO∥A'B',
∵OB'=OB=2 ,
∴OH= OB'= ,B'H= =3,
∴点B'的坐标为( ,3);
(Ⅱ)∵∠BOB'=∠AOA'=α,OB=OB',OA=OA',
∴∠OBB'=∠OA'A= (180°﹣α),
∵∠BOA'=90°+α,四边形OBPA'的内角和为360°,
∴∠BPA'=360°﹣(180°﹣α)﹣(90°+α)=90°,
∴AA'⊥BB';
(Ⅲ)如图,作AB的中点M(1, ),连接MP,
∵∠APB=90°,
∴点P的轨迹为以点M为圆心,以MP= AB=2为半径的圆,
∵C(﹣2,0),M(1, ),
∴CM= ,
∴当点P在CM延长线上时,线段CP长度最大,最大值为2 +2;
当点P在CM上时,线段CP长度最小,最小值为2 -2;
线段CP长度的取值范围:2 -2≤CP≤2 +2.
23.【答案】解:∵点A的坐标为(3,0),点B的坐标为(﹣3,0),
∴OA=OB=3,
∵AD⊥BC,
∴∠ADB=90°,
∴点D在以O为圆心,OA为半径的圆上,
如图,当点C'(0, )时,连接BC'交⊙O于点D',
∵tan∠D'BO= = ,
∴∠D'BO=30°,
∵BO=D'O,
∴∠BOD'=120°,
∵tan∠CBO= ,
∴∠CBO=60°,
∵BO=DO,
∴∠BOD=60°,
∴∠DOD'=60°,
∵点C坐标由(0, )到(0,3 ),
∴点D的运动的路径长= .
24.【答案】(1)①如图1中,连接 、 .
由题意: , △ 是直角三角形, ,即 , 是 的切线, .
② 在 上, , 是 的“2相关依附点”.
故答案为: ,是;
(2)①如图2,当 时,不妨设直线 与 相切的切点 在 轴上方(切点 在 轴下方时同理),连接 ,则 .
, , , , , ,此时 ;
②如图3中,若直线 与 不相切,设直线 与 的另一个交点为 (不妨设 ,点 , 在 轴下方时同理),作 于点 ,则 , , , , 当 时, ,此时 ,假设 经过点 ,此时 , 点 早 外, 的取值范围是 .
(3)如图4中,由(2)可知:当 时, .
当 时, 经过点 或 ,当直线 经过点 时, ,当直线 经过点 时, , 满足条件的 的取值范围为 .
25.【答案】(1)解:①点Q如下图所示.
∵点,
∴点向右平移1个单位长度,再向上平移1个单位长度,得到点,
∴,
∵点关于点的对称点为,,
∴点的横坐标为:,纵坐标为:,
∴点,在坐标系内找出该点即可;
②证明:如图延长ON至点,连接AQ,
∵,
∴,
在与中,
,
∴,
∴,
∵,,,
∴,,,
∴,
∴,
∴;
(2)解:长的最大值与最小值的差为.
26.【答案】(1)证明:∵ ,
∴
则在四边形 中
故四边形 为矩形
,
在 中,
∴ ,
∵
∴ ;
(2)解:①过点Q作 于S
由(1)得:
在 中,
∴
平移扫过面积:
旋转扫过面积:
故边PQ扫过的面积:
②运动分两个阶段:平移和旋转
平移阶段:
旋转阶段:
由线段长度得:
取刚开始旋转状态,以PM为直径作圆,则H为圆心,延长DK与圆相交于点G,连接GH,GM,过点G作 于T
设 ,则
在 中:
设 ,则 , ,
, ,
∵DM为直径
∴
在 中 :
在 中:
在 中:
∴ ,
PQ转过的角度:
s
总时间:
③
27.【答案】(1)解:如图,连接CP,
∵∠ABC=90°,AB=AC=2,
∴BC=4,
∵点P为FG的中点,线段EF绕点E顺时针旋转 90°得到线段EG,
∴△FEG为等腰直角三角形,EP⊥FG,
∵D为BC的中点,
∴PD=BC=×4=2;
(2)证明:如图,过点E作EH⊥AD的延长线于点H,
∴∠FEG=∠HEF=90°,
∴∠HEF+∠FEN=∠FEN+∠AEG,
∴∠HEF=∠AEG,
∵D为BC中点,∠ABC=90°,AB=AC=2,
∴∠HAE=∠H=45°,
∴AE=HE,
又∵FE=GE,
∴△FEH≌△GEA(SAS),
∴HF=AG,∠H=∠GAE,
∵HE∥BA,∠AGN=∠AEG
∴∠H=∠MAF=∠GAN,∠HEF=∠AMF=∠AEG=∠AGN,
又∵GN=MF,
∴△ANG≌△AFM(AAS),
∴AM=AG,
∴AM=HF,
∴AM+AF=HF+AF=AH=AE,
即AM+AF=AE;
(3)解: -
28.【答案】(1)解:如图1,作BM⊥x轴,垂足为M,根据题意AB=AE=EF=BF=,且∠EFO=∠BFM=45°,
∴∠EFB=90°,
∴四边形ABFE是正方形,
∴边AE,BF的中点所在直线就是与的一条“关联轴”;
∵的半径为1,
∴EH=GH=FG=EF==,且∠EFG=90°,
∴四边形EFGH是正方形,
∵∠EFG+∠EFB=180°,
∴B、F、G三点共线,
∴直线EF是与的一条“关联轴”.
(2)解:如图2,根据A(2,3),B(4,1),C(4,1),计算AB=,故AB不能落在圆的内部;
过点A作AN⊥y轴,垂足为N,则AN=2,等于圆的直径,存在“关联轴”使是的关联三角形,
此时;
作点B关于x轴的对称点P,此时BP=2,等于圆的直径,存在“关联轴”使是的关联三角形,此时,综上所述,点C横坐标的范围是.
(3)解:OC的最小值为;OC最大,根据勾股定理,AC=4.
二一教育在线组卷平台(zujuan.21cnjy.com)自动生成 1 / 1
专题训练:圆动点问题
一、单选题
1.如图,在矩形中,,,为矩形内一点,,连接,则的最小值为( )
A.8 B. C.10 D.
2.在Rt△ABC中,∠C=90°,AC=10,BC=12,点D为线段BC上一动点.以CD为⊙O直径,作AD交⊙O于点E,连BE,则BE的最小值为( )
A.6 B.8 C.10 D.12
3.如图,AB是半圆O的直径,点C在半圆O上,OA=10,BC=16,D是弧AC上一个动点,连接BD,过点C作CM⊥BD,连接AM,在点D移动的过程中,AM的最小值为( )
A. B. C. D.
4.如图,正比例函数y=2x与反比例函数的图象交于A、B两点,点P在以为圆心,1为半径的⊙C上运动,点Q是AP的中点,则OQ长的最大值为( )
A.2 B. C. D.
5.已知的直径,与的弦垂直,垂足为,且,则直径上的点(包含端点)与点的距离为整数的点有( )
A.1个 B.3个 C.6个 D.7个
6.如图,在中,,点O是的三等分点,半圆O与相切,M,N分别是与半圆弧上的动点,则的最小值和最大值之和是( )
A.8 B.10 C.12 D.14
7.如图,点A的坐标是( 2,0),点C是以OA为直径的⊙B上的一动点,点A关于点C的对称点为点P. 当点C在⊙ B上运动时,所有这样的点P组成的图形与直线y=kx-3(k>0)有且只有一个公共点,则k的值是()
A. B. C. D.
8.如图,在平面直角坐标系中,直线 分别与x轴、y轴相交于点A、B,点E、F分别是正方形 的边 、 上的动点,且 ,过原点O作 ,垂足为H,连接 、 ,则 面积的最大值为()
A. B.12 C. D.
9.如图, 是 的直径, , 是半径 上的一动点, 交 于点 ,在半径 上取点 ,使得 , 交 于点 ,点 位于 两侧,连结 交 于点 .点 从点 出发沿 向终点 运动,在整个运动过程中, 与 的面积和的变化情况是( )
A.一直减小 B.一直不变
C.先变大后变小 D.先变小后变大
10.在平行四边形中,,,,点E是边上的动点,过点B作直线的垂线,垂足为F,当点E从点A运动到点B时,点F的运动路径长为( )
A. B. C. D.2
二、填空题
11.如图,点,的坐标分别为,,为坐标平面内一动点,且,点为线段的中点,连接,当取最大值时,点的纵坐标为 .
12.如图,在矩形中,,,点,分别是,边上的动点,且,点为的中点,点为上的一动点,则的最小值为 .
13.如图,是的外接圆,为直径,若,,点从点出发,在内运动且始终保持,当,两点距离最小时,动点的运动路径长为 .
14.如图,在平面直角坐标系中,点A的坐标为,点B的坐标为,点C是线段AO上的一个动点,连接BC,于点D,以OD为一边,作正方形ODEF,其中点E与点B在直线OD两侧,当点C从点A运动到点O过程中,点E经过的路径长为 .
15.如图,在中,,将绕点顺时针旋转90°得到,为线段上的动点,以为圆心、为半径作⊙,当⊙与的边相切时,⊙的半径的长为 .
16.如图,、,以为直径作,射线交于、两点,为弧的中点,为的中点.当射线绕点旋转时,的最小值为 .
17.如图,直线l与圆O相交于A、B两点,AC是圆O的弦,OC∥AB,半径OC的长为10,弦AB的长为12,动点P从点A出发以每秒1个单位的速度沿射线AB方向运动.当△APC是直角三角形时,动点P运动的时间t为 秒.
18.图,在⊙O中,AC,BD是直径,∠BOC=60°,点P是劣弧AB上任意一点(不与A、B重合),过点P作AC垂线,交AC、BD所在直线于点E,F,过点P作BD垂线,交BD、AC所在直线于点G、H,下列选项中,正确的是 .
①;②∠GPE=60°;③PG+PE最大值为;④当△PEH≌△CBA时,.
19.如图,在直角坐标系中,的圆心A的坐标为(1,0),半径为1,点P为直线上的动点,过点P作的切线,切点为Q,则切线长PQ的最小值是 .
20.如图,在矩形中,,,点E、F分别是边、上的动点,且,点G是的中点,、,则四边形面积的最小值为 .
三、解答题
21.如图,在直角坐标系中,直线 与 轴交于 点,与 轴交于 点,以 为直径作圆 ,过 作圆 的切线交 轴于点 .
(1)求 点的坐标;
(2)设点 为 延长线上一点, , 为线段 上的一个动点(异于 , ),过 点作 轴的平行线交 于 ,交 的延长线于 ,试判断 的值是否为定值,如果是,则求出这个值;如果不是,请说明理由.
22.在平面直角坐标系中,已知点A(2,0),点B(0, ).点O(0,0).△AOB绕着点O顺时针旋转,得到△A'OB',点A、B旋转后的对应点为A'、B',记旋转角为α.
(Ⅰ)如图1,若α=30°,求点B'的坐标;
(Ⅱ)如图2,若0°<α<90°,设直线AA'和直线BB'交于点P,求证:AA'⊥BB';
(Ⅲ)在(Ⅱ)中的条件下,若0°<α<360°,点C(﹣2,0).求线段CP长度的取值范围.(直接写出结果即可)
23.如图,在平面直角坐标系中,点A的坐标为(3,0),点B的坐标为(﹣3,0).过点B的直线绕点B逆时针方向旋转,过程中与y轴交于点C.过点A作AD⊥BC于点D,求在点C坐标由(0, )到(0,3 )的过程中点D运动的路径长.
24.对于平面内的⊙C和⊙C外一点Q,给出如下定义:若过点Q的直线与⊙C存在公共点,记为点A,B,设 ,则称点A(或点B)是⊙C的“K相关依附点”,特别地,当点A和点B重合时,规定AQ=BQ, (或 ).
已知在平面直角坐标系xOy中,Q(-1,0),C(1,0),⊙C的半径为r.
(1)如图1,当 时,
①若A1(0,1)是⊙C的“k相关依附点”,求k的值.
②A2(1+ ,0)是否为⊙C的“2相关依附点”.
(2)若⊙C上存在“k相关依附点”点M,
①当r=1,直线QM与⊙C相切时,求k的值.
②当 时,求r的取值范围.
(3)若存在r的值使得直线 与⊙C有公共点,且公共点时⊙C的“ 相关依附点”,直接写出b的取值范围.
四、综合题
25.在平面直角坐标系中,已知点对于点给出如下定义:将点向右或向左平移个单位长度,再向上或向下平移个单位长度,得到点,点关于点的对称点为,称点为点的“对应点”.
(1)如图,点点在线段的延长线上,若点点为点的“对应点”.
①在图中画出点;
②连接交线段于点求证:
(2)的半径为1,是上一点,点在线段上,且,若为外一点,点为点的“对应点”,连接当点在上运动时直接写出长的最大值与最小值的差(用含的式子表示)
26.如图,四边形ABCD中, ,∠ABC=90°,∠C=30°,AD=3, ,DH⊥BC于点H.将△PQM与该四边形按如图方式放在同一平面内,使点P与A重合,点B在PM上,其中∠Q=90°,∠QPM=30°, .
(1)求证:△PQM≌△CHD;
(2)△PQM从图1的位置出发,先沿着BC方向向右平移(图2),当点P到达点D后立刻绕点D逆时针旋转(图3),当边PM旋转50°时停止.
①边PQ从平移开始,到绕点D旋转结束,求边PQ扫过的面积;
②如图2,点K在BH上,且 .若△PQM右移的速度为每秒1个单位长,绕点D旋转的速度为每秒5°,求点K在△PQM区域(含边界)内的时长;
③如图3.在△PQM旋转过程中,设PQ,PM分别交BC于点E,F,若BE=d,直接写出CF的长(用含d的式子表示).
27.在△ ABC中,∠BAC=90° ,AB=AC= ,D为 BC的中点,E,F分别为AC, AD 上任意一点,连接EF,将线段EF绕点E顺时针旋转 90°得到线段EG,连接FG, AG.
(1)如图1,点 E 与点 C 重合,且 GF 的延长线过点 B ,若点 P 为 FG 的中点,连接 PD,求 PD的长;
(2)如图 2,EF 的延长线交 AB 于点M,点N在 AC上, ∠AGN=∠AEG 且GN=MF,求证:AM+AF= AE
(3)如图3,F为线段 AD上一动点,E为 AC的中点,连接BE,H为直线BC上一动点,连接 EH,将△ BEH沿EH翻折至△ABC所在平面内,得到△ B'EH',连接 B'G,直接写出线段 B'G的长度的最小值
28.在平面直角坐标系中,的半径为1,对于和直线给出如下定义:若的一条边关于直线的对称线段是的弦,则称是的关于直线的“关联三角形”,直线是“关联轴”.
(1)如图1,若是的关于直线的“关联三角形”,请画出与的“关联轴”(至少画两条);
(2)若中,点坐标为,点坐标为,点在直线的图像上,存在“关联轴”使是的关联三角形,求点横坐标的取值范围;
(3)已知,将点向上平移2个单位得到点,以为圆心为半径画圆,,为上的两点,且(点在点右侧),若与的关联轴至少有两条,直接写出的最小值和最大值,以及最大时的长.
答案解析部分
1.【答案】A
2.【答案】B
3.【答案】D
4.【答案】D
5.【答案】C
6.【答案】C
7.【答案】D
8.【答案】D
9.【答案】B
10.【答案】B
11.【答案】
12.【答案】8
13.【答案】
14.【答案】
15.【答案】或
16.【答案】
17.【答案】16或20
18.【答案】①②④
19.【答案】
20.【答案】38
21.【答案】(1)∵BC是圆的切线,
∴BC⊥AB,
∵直线AB的解析式为,
∴直线BC的解析式为y=2x+4,令y=0,
∴2x+4=0,∴x=-2,
∴C(-2,0);
(2)PM+PN的值是定值,定值为20。将x=0代入直线,得到y=4,
∴B(4,0),再将y=0代入直线,得到x=8,
∴A(8,0),由(1)可知:C(-2,0),∵CDBC,
∴D(-4,-4),∵A(8,0),
∴直线AD的解析式为,
∵点P再线段BC上,设P(m,2m+4)(-2
∴M(-4m,2m+4),N(6m+20,2m+4),
∴PM+PN=-4m-m+(6m+20-m)=20,即:PM+PN的值是定值,定值为20.
22.【答案】解:(Ⅰ)如图1,设A'B'与x轴交于点H,
∵OA=2,OB=2 ,∠AOB=90°,
∴AB=4,
∴∠ABO=∠B'=30°,
∵∠BOB'=α=30°,
∴BO∥A'B',
∵OB'=OB=2 ,
∴OH= OB'= ,B'H= =3,
∴点B'的坐标为( ,3);
(Ⅱ)∵∠BOB'=∠AOA'=α,OB=OB',OA=OA',
∴∠OBB'=∠OA'A= (180°﹣α),
∵∠BOA'=90°+α,四边形OBPA'的内角和为360°,
∴∠BPA'=360°﹣(180°﹣α)﹣(90°+α)=90°,
∴AA'⊥BB';
(Ⅲ)如图,作AB的中点M(1, ),连接MP,
∵∠APB=90°,
∴点P的轨迹为以点M为圆心,以MP= AB=2为半径的圆,
∵C(﹣2,0),M(1, ),
∴CM= ,
∴当点P在CM延长线上时,线段CP长度最大,最大值为2 +2;
当点P在CM上时,线段CP长度最小,最小值为2 -2;
线段CP长度的取值范围:2 -2≤CP≤2 +2.
23.【答案】解:∵点A的坐标为(3,0),点B的坐标为(﹣3,0),
∴OA=OB=3,
∵AD⊥BC,
∴∠ADB=90°,
∴点D在以O为圆心,OA为半径的圆上,
如图,当点C'(0, )时,连接BC'交⊙O于点D',
∵tan∠D'BO= = ,
∴∠D'BO=30°,
∵BO=D'O,
∴∠BOD'=120°,
∵tan∠CBO= ,
∴∠CBO=60°,
∵BO=DO,
∴∠BOD=60°,
∴∠DOD'=60°,
∵点C坐标由(0, )到(0,3 ),
∴点D的运动的路径长= .
24.【答案】(1)①如图1中,连接 、 .
由题意: , △ 是直角三角形, ,即 , 是 的切线, .
② 在 上, , 是 的“2相关依附点”.
故答案为: ,是;
(2)①如图2,当 时,不妨设直线 与 相切的切点 在 轴上方(切点 在 轴下方时同理),连接 ,则 .
, , , , , ,此时 ;
②如图3中,若直线 与 不相切,设直线 与 的另一个交点为 (不妨设 ,点 , 在 轴下方时同理),作 于点 ,则 , , , , 当 时, ,此时 ,假设 经过点 ,此时 , 点 早 外, 的取值范围是 .
(3)如图4中,由(2)可知:当 时, .
当 时, 经过点 或 ,当直线 经过点 时, ,当直线 经过点 时, , 满足条件的 的取值范围为 .
25.【答案】(1)解:①点Q如下图所示.
∵点,
∴点向右平移1个单位长度,再向上平移1个单位长度,得到点,
∴,
∵点关于点的对称点为,,
∴点的横坐标为:,纵坐标为:,
∴点,在坐标系内找出该点即可;
②证明:如图延长ON至点,连接AQ,
∵,
∴,
在与中,
,
∴,
∴,
∵,,,
∴,,,
∴,
∴,
∴;
(2)解:长的最大值与最小值的差为.
26.【答案】(1)证明:∵ ,
∴
则在四边形 中
故四边形 为矩形
,
在 中,
∴ ,
∵
∴ ;
(2)解:①过点Q作 于S
由(1)得:
在 中,
∴
平移扫过面积:
旋转扫过面积:
故边PQ扫过的面积:
②运动分两个阶段:平移和旋转
平移阶段:
旋转阶段:
由线段长度得:
取刚开始旋转状态,以PM为直径作圆,则H为圆心,延长DK与圆相交于点G,连接GH,GM,过点G作 于T
设 ,则
在 中:
设 ,则 , ,
, ,
∵DM为直径
∴
在 中 :
在 中:
在 中:
∴ ,
PQ转过的角度:
s
总时间:
③
27.【答案】(1)解:如图,连接CP,
∵∠ABC=90°,AB=AC=2,
∴BC=4,
∵点P为FG的中点,线段EF绕点E顺时针旋转 90°得到线段EG,
∴△FEG为等腰直角三角形,EP⊥FG,
∵D为BC的中点,
∴PD=BC=×4=2;
(2)证明:如图,过点E作EH⊥AD的延长线于点H,
∴∠FEG=∠HEF=90°,
∴∠HEF+∠FEN=∠FEN+∠AEG,
∴∠HEF=∠AEG,
∵D为BC中点,∠ABC=90°,AB=AC=2,
∴∠HAE=∠H=45°,
∴AE=HE,
又∵FE=GE,
∴△FEH≌△GEA(SAS),
∴HF=AG,∠H=∠GAE,
∵HE∥BA,∠AGN=∠AEG
∴∠H=∠MAF=∠GAN,∠HEF=∠AMF=∠AEG=∠AGN,
又∵GN=MF,
∴△ANG≌△AFM(AAS),
∴AM=AG,
∴AM=HF,
∴AM+AF=HF+AF=AH=AE,
即AM+AF=AE;
(3)解: -
28.【答案】(1)解:如图1,作BM⊥x轴,垂足为M,根据题意AB=AE=EF=BF=,且∠EFO=∠BFM=45°,
∴∠EFB=90°,
∴四边形ABFE是正方形,
∴边AE,BF的中点所在直线就是与的一条“关联轴”;
∵的半径为1,
∴EH=GH=FG=EF==,且∠EFG=90°,
∴四边形EFGH是正方形,
∵∠EFG+∠EFB=180°,
∴B、F、G三点共线,
∴直线EF是与的一条“关联轴”.
(2)解:如图2,根据A(2,3),B(4,1),C(4,1),计算AB=,故AB不能落在圆的内部;
过点A作AN⊥y轴,垂足为N,则AN=2,等于圆的直径,存在“关联轴”使是的关联三角形,
此时;
作点B关于x轴的对称点P,此时BP=2,等于圆的直径,存在“关联轴”使是的关联三角形,此时,综上所述,点C横坐标的范围是.
(3)解:OC的最小值为;OC最大,根据勾股定理,AC=4.
二一教育在线组卷平台(zujuan.21cnjy.com)自动生成 1 / 1
同课章节目录
