浙教版数学九下第二章 直线与圆的位置关系 精题精练(含答案)
文档属性
| 名称 | 浙教版数学九下第二章 直线与圆的位置关系 精题精练(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 215.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-20 19:33:43 | ||
图片预览



文档简介
登录二一教育在线组卷平台 助您教考全无忧
浙教版数学九下第二单元精题精练
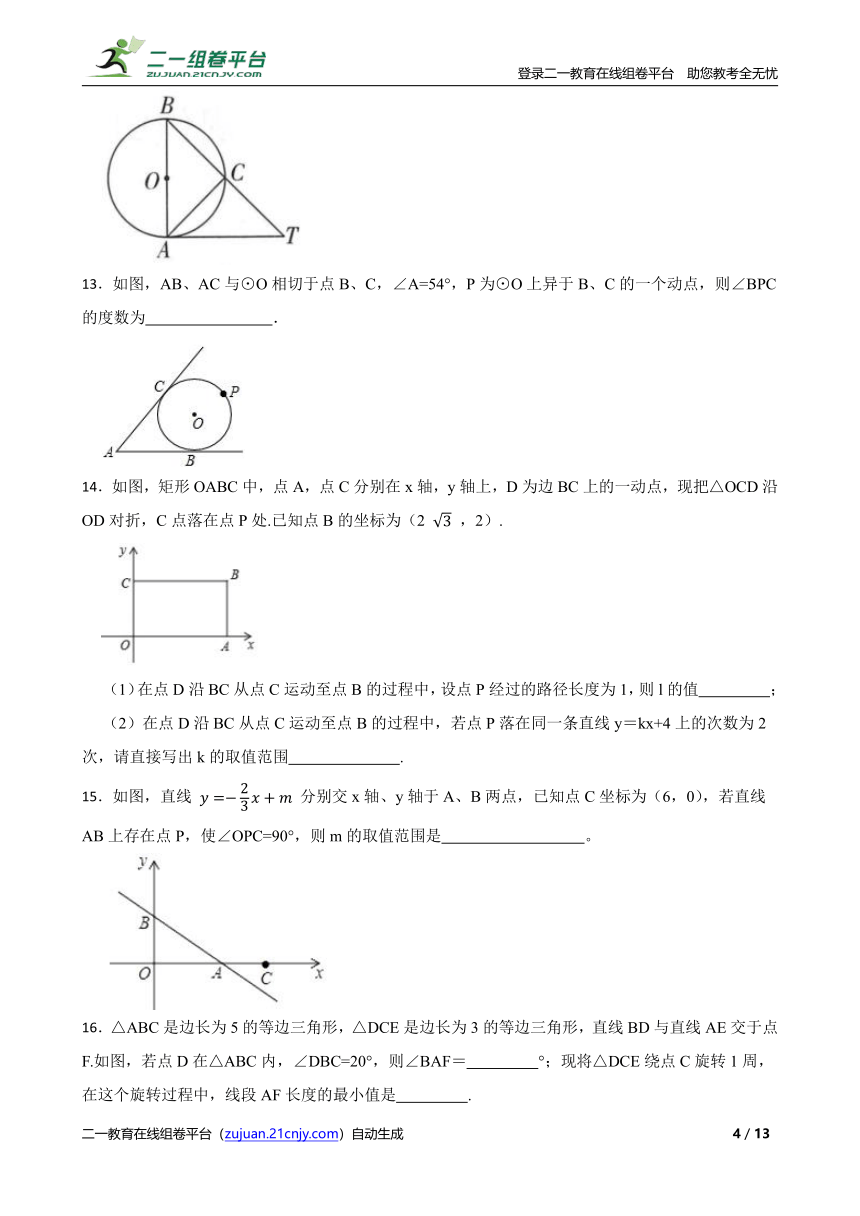
一、单选题(共10题;共40分)
1.如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E交PA,PB于C,D,若⊙O的半径为r,△PCD的周长为3r,连接OA,OP,则的值是( )
A. B. C. D.
2.如图所示,AB是⊙O的直径,AM、BN是⊙O的两条切线,D、C分别在AM、BN上,DC切⊙O于点E,连接OD、OC、BE、AE,BE与OC相交于点P,AE与OD相交于点Q,已知AD=4,BC=9,以下结论:
①⊙O的半径为 ②OD∥BE ③PB= ④tan∠CEP=
其中正确结论有( )
A.1个 B.2个 C.3个 D.4个
3.如图,AB是⊙O的直径,AC是⊙O的切线,BC与⊙O相交于D,连接AD、OD(AC≠AB),则能够判断图中∠B的余角(不再添加任何辅助线)的有( )
A.1个 B.2个 C.3个 D.4个
4.如图,PA,PB分别与⊙O相切于A,B两点,若∠C=65°,则∠P的度数为( )
A.65° B.130° C.50° D.100°
5.如图,⊙M与x轴相切于原点,平行于y轴的直线交圆于P、Q两点,P在Q点的下方,若P点的坐标是(2,1),则圆心M的坐标是( )
A.(0,3) B.(0,2) C.(0,) D.(0,)
6.如图,在中,,,,点O是AB的三等分点,半圆O与AC相切,M,N分别是BC与半圆弧上的动点,则MN的最小值和最大值之和是( )
A.5 B.6 C.7 D.8
7.如图, 是等腰三角形, ,以斜边AB上的点O为圆心的圆分别与AC、BC相切于点D、E,与AB分别相交于点G、H,且DG的延长线与CB的延长线交于点F,分析下列四个结论:① ;② ;③ .其中正确的结论个数有( )
A.1个 B.2个 C.3个 D.0个
8.如图,在直角边分别为3和4的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,以此类推,依此类推,图10中有10个直角三角形的内切圆,它们的面积分别记为S1,S2,S3,…,S10,则S1+S2+S3+…+S10=( )
A.4π B.3π C.2π D.π
9.如图所示,在平面直角坐标系中,⊙O的半径为1,点P在经过点A(﹣3,0),B(0,4)的直线上,PQ切⊙O于点Q,则切线长PQ的最小值为( )
A. B.2.4 C. D.3
10.如图,⊙O的半径为2,点O到直线l的距离为3,点P是直线l上的一个动点,PQ切⊙O于点Q,则PQ的最小值为( )
A. B. C.3 D.5
二、填空题(共6题;共30分)
11.如图,在△ABC中,∠C=90°,AB=10, ,经过点C且与边AB相切的动圆与CA、CB分别交于点D、E,则线段DE长度的最小值是 .
12.在下图中,是的直径,要使得直线是的切线,需要添加的一个条件是 .(写一个条件即可)
13.如图,AB、AC与⊙O相切于点B、C,∠A=54°,P为⊙O上异于B、C的一个动点,则∠BPC的度数为 .
14.如图,矩形OABC中,点A,点C分别在x轴,y轴上,D为边BC上的一动点,现把△OCD沿OD对折,C点落在点P处.已知点B的坐标为(2 ,2).
(1)在点D沿BC从点C运动至点B的过程中,设点P经过的路径长度为1,则l的值 ;
(2)在点D沿BC从点C运动至点B的过程中,若点P落在同一条直线y=kx+4上的次数为2次,请直接写出k的取值范围 .
15.如图,直线 分别交x轴、y轴于A、B两点,已知点C坐标为(6,0),若直线AB上存在点P,使∠OPC=90°,则m的取值范围是 。
16.△ABC是边长为5的等边三角形,△DCE是边长为3的等边三角形,直线BD与直线AE交于点F.如图,若点D在△ABC内,∠DBC=20°,则∠BAF= °;现将△DCE绕点C旋转1周,在这个旋转过程中,线段AF长度的最小值是 .
三、解答题(共8题;共80分)
17.已知:如图,在 中, ,以 为直径的 交 于点 ,过点 作 于点 .求证: 是 的切线.
18.如图,⊙O是以数轴原点O为圆心,半径为1的圆,∠AOB=45°,点P在数轴上运动,过点P且与OB平行的直线与⊙O有公共点,求OP的取值范围.
19.如图,AB是⊙O的切线,B为切点,圆心O在AC上,∠A=30°,D为的中点.
(1)求证:AB=BC.
(2)试判断四边形BOCD的形状,并说明理由.
20.如图,在△ABC中,∠ACB=90°,E为BC上一点,以CE为直径作⊙O,AB与⊙O相切于点D,连接CD,若BE=OE=2.
(1)求证:∠A=2∠DCB;
(2)求图中阴影部分的面积(结果保留和根号).
21.如图,在△ABC中,∠ABC=90°,以AB为直径的⊙O与AC边交于点D,过点D的直线交BC边于点E,∠BDE=∠A.
(1)判断直线DE与⊙O的位置关系,并说明理由.
(2)若⊙O的半径R=5,tanA=,求线段CD的长.
22.如图,AB,CD是⊙O的直径,点E在AB延长线上,FE⊥AB,BE=EF=2,FE的延长线交CD延长线于点G,DG=GE=3,连接FD.
(1)求⊙O的半径;
(2)求证:DF是⊙O的切线.
23.如图所示, 中,∠BAC=90°,∠C=30°,BC=2,⊙O是△ABC的外接圆,D是CB延长线上一点,且BD=1,连接DA,点P是射线DA上的动点。
(1)求证DA是⊙O的切线;
(2)DP的长度为多少时,∠BPC的度数最大,最大度数是多少?请说明理由。
(3)点P运动的过程中,(PB+PC)的值能否达到最小,若能,求出这个最小值,若不能,说明理由.
24.在 中,弦 与直径 相交于点P, .
(1)如图①,若 ,求 和 的大小;
(2)如图②,若 ,过点D作 的切线,与 的延长线相交于点E,求 的大小.
答案解析部分
1.【答案】D
2.【答案】C
3.【答案】C
4.【答案】C
5.【答案】C
6.【答案】B
7.【答案】C
8.【答案】D
9.【答案】C
10.【答案】B
11.【答案】4.8
12.【答案】∠ABT=∠ATB=45°(答案不唯一)
13.【答案】63°或117°
14.【答案】(1)
(2)
15.【答案】
16.【答案】80;
17.【答案】解:连接OD.
∵OD=OB,∴∠B=∠ODB.
∵AB=AC,∴∠B=∠C,∴∠C=∠ODB,∴OD∥AC,∴∠ODE=∠DEC;
∵DE⊥AC,∴∠DEC=90°,∴∠ODE=90°,即DE⊥OD,∴DE是⊙O的切线.
18.【答案】解:如图,平移过P点的直线到P′,使其与⊙O相切,设切点为Q,连接OQ,
由切线的性质,得∠OQP′=90°,
∵OB∥P′Q,
∴∠OP′Q=∠AOB=45°,
∴△OQP′为等腰直角三角形,
在Rt△OQP′中,OQ=1,
OP′= =
∴当过点P且与OB平行的直线与⊙O有公共点时,0<OP≤
当点P在x轴负半轴即点P向左侧移动时,结果相同.
故答案为:0<OP≤
19.【答案】解:(1)∵AB是⊙O的切线,∴∠OBA=90°,∠AOB=90°﹣30°=60°.∵OB=OC,∴∠OBC=∠OCB,∠OCB=30°=∠A,∴AB=BC.(2)四边形BOCD为菱形,理由如下:连接OD交BC于点M,∵D是的中点,∴OD垂直平分BC.在Rt△OMC中,∵∠OCM=30°,∴OC=2OM=OD∴OM=MD,∴四边形BOCD为菱形.
20.【答案】(1)证明:连接OD.
∵AB与⊙O相切于点D,
∴ OD⊥AB,
∴∠B+∠DOB=90°.
∵∠ACB=90°,
∴∠A+∠B=90°,
∴∠A=∠DOB.
∵OC=OD,
∴∠DOB=2∠DCB.
∴∠A=2∠DCB.
(2)解:在Rt△ODB中,
∵OD=OE,OE=BE,
∴sin∠B=,
∴∠B=30°,∠DOB=60°.
∵BD=OB·sin60°=,
∴,SDOB=,S扇形ODE=.
∴S阴影=SDOB-S扇形ODE=.
21.【答案】解:(1)直线DE与⊙O相切.
理由如下:连接OD.
∵OA=OD
∴∠ODA=∠A
又∵∠BDE=∠A
∴∠ODA=∠BDE
∵AB是⊙O直径
∴∠ADB=90°
即∠ODA+∠ODB=90°
∴∠BDE+∠ODB=90°
∴∠ODE=90°
∴OD⊥DE
∴DE与⊙O相切;
(2)∵R=5,
∴AB=10,
在Rt△ABC中
∵tanA==
∴BC=AB tanA=10×=,
∴AC===,
∵∠BDC=∠ABC=90°,∠BCD=∠ACB
∴△BCD∽△ACB
∴
∴CD===.
22.【答案】(1)解:设⊙0半径为R,则OD=OB=R,
在Rt△OEG中,∠OEG=90°,由勾股定理得:OG2=OE2+EG2,
∴(R+3)2=(R+2)2+32,
R=2,
即⊙O半径是2.
(2)证明:∵OB=OD=2,
∴OG=2+3=5,GF=2+3=5=OG,
∵在△FDG和△OEG中
∴△FDG≌△OEG(SAS),
∴∠FDG=∠OEG=90°,
∴∠ODF=90°,
∴OD⊥DF,
∵OD为半径,
∴DF是⊙O的切线.
23.【答案】(1)证明:连接AO,易知:△ABO是等边三角形,AB=BD=1;∴∠ADC=∠DAC=∠ABO=30°,而∠AOD=60°;∴∠DAO=90°
∴DA是⊙o的切线;
(2)解:当点P运动到A处时,即DP=DA=时,∠BPC的度数达到最大,最大值为90°.理由如下:
若点P不在A处时,不妨设点P在DA的延长线上,连接BP,与⊙o交于一点,记为点E,连接CE,
∴∠BPC<∠BEC=∠BAC=90°;
(3)解:作点C关于射线DA的对称点C′,则BP+PC=BP+PC′,当点C′,P,B三点共线时,(PB+PC)的值达到最小,最小为BC.
过点作DC的垂线,垂足记为点H,连接DC′;
在Rt△DCP中,∠PDC=30°;
∴△DCC′为等边三角形,
∴H为DC的中点,
∴BH=DH-DB=CD-DB=-1=;
∴C′H=DH=;
由勾股定理求出:BC′=;
∴(PB+PC)的最小值为;
24.【答案】(1)解: 是 的一个外角, , ,
.
在 中, ,
.
为 的直径,
.
在 中, ,
又 ,
.
(2)如下图所示,连接OD,
,
.
.
在 中,由同弧所对的圆周角等于圆心角的一半可知:
,
∴ ,
是 的切线,
.即 ,
,
.
故答案为: .
二一教育在线组卷平台(zujuan.21cnjy.com)自动生成 1 / 1
浙教版数学九下第二单元精题精练
一、单选题(共10题;共40分)
1.如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E交PA,PB于C,D,若⊙O的半径为r,△PCD的周长为3r,连接OA,OP,则的值是( )
A. B. C. D.
2.如图所示,AB是⊙O的直径,AM、BN是⊙O的两条切线,D、C分别在AM、BN上,DC切⊙O于点E,连接OD、OC、BE、AE,BE与OC相交于点P,AE与OD相交于点Q,已知AD=4,BC=9,以下结论:
①⊙O的半径为 ②OD∥BE ③PB= ④tan∠CEP=
其中正确结论有( )
A.1个 B.2个 C.3个 D.4个
3.如图,AB是⊙O的直径,AC是⊙O的切线,BC与⊙O相交于D,连接AD、OD(AC≠AB),则能够判断图中∠B的余角(不再添加任何辅助线)的有( )
A.1个 B.2个 C.3个 D.4个
4.如图,PA,PB分别与⊙O相切于A,B两点,若∠C=65°,则∠P的度数为( )
A.65° B.130° C.50° D.100°
5.如图,⊙M与x轴相切于原点,平行于y轴的直线交圆于P、Q两点,P在Q点的下方,若P点的坐标是(2,1),则圆心M的坐标是( )
A.(0,3) B.(0,2) C.(0,) D.(0,)
6.如图,在中,,,,点O是AB的三等分点,半圆O与AC相切,M,N分别是BC与半圆弧上的动点,则MN的最小值和最大值之和是( )
A.5 B.6 C.7 D.8
7.如图, 是等腰三角形, ,以斜边AB上的点O为圆心的圆分别与AC、BC相切于点D、E,与AB分别相交于点G、H,且DG的延长线与CB的延长线交于点F,分析下列四个结论:① ;② ;③ .其中正确的结论个数有( )
A.1个 B.2个 C.3个 D.0个
8.如图,在直角边分别为3和4的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,以此类推,依此类推,图10中有10个直角三角形的内切圆,它们的面积分别记为S1,S2,S3,…,S10,则S1+S2+S3+…+S10=( )
A.4π B.3π C.2π D.π
9.如图所示,在平面直角坐标系中,⊙O的半径为1,点P在经过点A(﹣3,0),B(0,4)的直线上,PQ切⊙O于点Q,则切线长PQ的最小值为( )
A. B.2.4 C. D.3
10.如图,⊙O的半径为2,点O到直线l的距离为3,点P是直线l上的一个动点,PQ切⊙O于点Q,则PQ的最小值为( )
A. B. C.3 D.5
二、填空题(共6题;共30分)
11.如图,在△ABC中,∠C=90°,AB=10, ,经过点C且与边AB相切的动圆与CA、CB分别交于点D、E,则线段DE长度的最小值是 .
12.在下图中,是的直径,要使得直线是的切线,需要添加的一个条件是 .(写一个条件即可)
13.如图,AB、AC与⊙O相切于点B、C,∠A=54°,P为⊙O上异于B、C的一个动点,则∠BPC的度数为 .
14.如图,矩形OABC中,点A,点C分别在x轴,y轴上,D为边BC上的一动点,现把△OCD沿OD对折,C点落在点P处.已知点B的坐标为(2 ,2).
(1)在点D沿BC从点C运动至点B的过程中,设点P经过的路径长度为1,则l的值 ;
(2)在点D沿BC从点C运动至点B的过程中,若点P落在同一条直线y=kx+4上的次数为2次,请直接写出k的取值范围 .
15.如图,直线 分别交x轴、y轴于A、B两点,已知点C坐标为(6,0),若直线AB上存在点P,使∠OPC=90°,则m的取值范围是 。
16.△ABC是边长为5的等边三角形,△DCE是边长为3的等边三角形,直线BD与直线AE交于点F.如图,若点D在△ABC内,∠DBC=20°,则∠BAF= °;现将△DCE绕点C旋转1周,在这个旋转过程中,线段AF长度的最小值是 .
三、解答题(共8题;共80分)
17.已知:如图,在 中, ,以 为直径的 交 于点 ,过点 作 于点 .求证: 是 的切线.
18.如图,⊙O是以数轴原点O为圆心,半径为1的圆,∠AOB=45°,点P在数轴上运动,过点P且与OB平行的直线与⊙O有公共点,求OP的取值范围.
19.如图,AB是⊙O的切线,B为切点,圆心O在AC上,∠A=30°,D为的中点.
(1)求证:AB=BC.
(2)试判断四边形BOCD的形状,并说明理由.
20.如图,在△ABC中,∠ACB=90°,E为BC上一点,以CE为直径作⊙O,AB与⊙O相切于点D,连接CD,若BE=OE=2.
(1)求证:∠A=2∠DCB;
(2)求图中阴影部分的面积(结果保留和根号).
21.如图,在△ABC中,∠ABC=90°,以AB为直径的⊙O与AC边交于点D,过点D的直线交BC边于点E,∠BDE=∠A.
(1)判断直线DE与⊙O的位置关系,并说明理由.
(2)若⊙O的半径R=5,tanA=,求线段CD的长.
22.如图,AB,CD是⊙O的直径,点E在AB延长线上,FE⊥AB,BE=EF=2,FE的延长线交CD延长线于点G,DG=GE=3,连接FD.
(1)求⊙O的半径;
(2)求证:DF是⊙O的切线.
23.如图所示, 中,∠BAC=90°,∠C=30°,BC=2,⊙O是△ABC的外接圆,D是CB延长线上一点,且BD=1,连接DA,点P是射线DA上的动点。
(1)求证DA是⊙O的切线;
(2)DP的长度为多少时,∠BPC的度数最大,最大度数是多少?请说明理由。
(3)点P运动的过程中,(PB+PC)的值能否达到最小,若能,求出这个最小值,若不能,说明理由.
24.在 中,弦 与直径 相交于点P, .
(1)如图①,若 ,求 和 的大小;
(2)如图②,若 ,过点D作 的切线,与 的延长线相交于点E,求 的大小.
答案解析部分
1.【答案】D
2.【答案】C
3.【答案】C
4.【答案】C
5.【答案】C
6.【答案】B
7.【答案】C
8.【答案】D
9.【答案】C
10.【答案】B
11.【答案】4.8
12.【答案】∠ABT=∠ATB=45°(答案不唯一)
13.【答案】63°或117°
14.【答案】(1)
(2)
15.【答案】
16.【答案】80;
17.【答案】解:连接OD.
∵OD=OB,∴∠B=∠ODB.
∵AB=AC,∴∠B=∠C,∴∠C=∠ODB,∴OD∥AC,∴∠ODE=∠DEC;
∵DE⊥AC,∴∠DEC=90°,∴∠ODE=90°,即DE⊥OD,∴DE是⊙O的切线.
18.【答案】解:如图,平移过P点的直线到P′,使其与⊙O相切,设切点为Q,连接OQ,
由切线的性质,得∠OQP′=90°,
∵OB∥P′Q,
∴∠OP′Q=∠AOB=45°,
∴△OQP′为等腰直角三角形,
在Rt△OQP′中,OQ=1,
OP′= =
∴当过点P且与OB平行的直线与⊙O有公共点时,0<OP≤
当点P在x轴负半轴即点P向左侧移动时,结果相同.
故答案为:0<OP≤
19.【答案】解:(1)∵AB是⊙O的切线,∴∠OBA=90°,∠AOB=90°﹣30°=60°.∵OB=OC,∴∠OBC=∠OCB,∠OCB=30°=∠A,∴AB=BC.(2)四边形BOCD为菱形,理由如下:连接OD交BC于点M,∵D是的中点,∴OD垂直平分BC.在Rt△OMC中,∵∠OCM=30°,∴OC=2OM=OD∴OM=MD,∴四边形BOCD为菱形.
20.【答案】(1)证明:连接OD.
∵AB与⊙O相切于点D,
∴ OD⊥AB,
∴∠B+∠DOB=90°.
∵∠ACB=90°,
∴∠A+∠B=90°,
∴∠A=∠DOB.
∵OC=OD,
∴∠DOB=2∠DCB.
∴∠A=2∠DCB.
(2)解:在Rt△ODB中,
∵OD=OE,OE=BE,
∴sin∠B=,
∴∠B=30°,∠DOB=60°.
∵BD=OB·sin60°=,
∴,SDOB=,S扇形ODE=.
∴S阴影=SDOB-S扇形ODE=.
21.【答案】解:(1)直线DE与⊙O相切.
理由如下:连接OD.
∵OA=OD
∴∠ODA=∠A
又∵∠BDE=∠A
∴∠ODA=∠BDE
∵AB是⊙O直径
∴∠ADB=90°
即∠ODA+∠ODB=90°
∴∠BDE+∠ODB=90°
∴∠ODE=90°
∴OD⊥DE
∴DE与⊙O相切;
(2)∵R=5,
∴AB=10,
在Rt△ABC中
∵tanA==
∴BC=AB tanA=10×=,
∴AC===,
∵∠BDC=∠ABC=90°,∠BCD=∠ACB
∴△BCD∽△ACB
∴
∴CD===.
22.【答案】(1)解:设⊙0半径为R,则OD=OB=R,
在Rt△OEG中,∠OEG=90°,由勾股定理得:OG2=OE2+EG2,
∴(R+3)2=(R+2)2+32,
R=2,
即⊙O半径是2.
(2)证明:∵OB=OD=2,
∴OG=2+3=5,GF=2+3=5=OG,
∵在△FDG和△OEG中
∴△FDG≌△OEG(SAS),
∴∠FDG=∠OEG=90°,
∴∠ODF=90°,
∴OD⊥DF,
∵OD为半径,
∴DF是⊙O的切线.
23.【答案】(1)证明:连接AO,易知:△ABO是等边三角形,AB=BD=1;∴∠ADC=∠DAC=∠ABO=30°,而∠AOD=60°;∴∠DAO=90°
∴DA是⊙o的切线;
(2)解:当点P运动到A处时,即DP=DA=时,∠BPC的度数达到最大,最大值为90°.理由如下:
若点P不在A处时,不妨设点P在DA的延长线上,连接BP,与⊙o交于一点,记为点E,连接CE,
∴∠BPC<∠BEC=∠BAC=90°;
(3)解:作点C关于射线DA的对称点C′,则BP+PC=BP+PC′,当点C′,P,B三点共线时,(PB+PC)的值达到最小,最小为BC.
过点作DC的垂线,垂足记为点H,连接DC′;
在Rt△DCP中,∠PDC=30°;
∴△DCC′为等边三角形,
∴H为DC的中点,
∴BH=DH-DB=CD-DB=-1=;
∴C′H=DH=;
由勾股定理求出:BC′=;
∴(PB+PC)的最小值为;
24.【答案】(1)解: 是 的一个外角, , ,
.
在 中, ,
.
为 的直径,
.
在 中, ,
又 ,
.
(2)如下图所示,连接OD,
,
.
.
在 中,由同弧所对的圆周角等于圆心角的一半可知:
,
∴ ,
是 的切线,
.即 ,
,
.
故答案为: .
二一教育在线组卷平台(zujuan.21cnjy.com)自动生成 1 / 1
