第五章 一次函数 章末复习----数学是清楚的 课件(共14张PPT)
文档属性
| 名称 | 第五章 一次函数 章末复习----数学是清楚的 课件(共14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 231.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-20 00:00:00 | ||
图片预览



文档简介
(共14张PPT)
浙教版八上数学
第五章 一次函数 章末复习
数学是清楚的--------知识来龙去脉是清楚的
几何直观 + 代数推理-------完美融合
1.函数 y=5x-3,k=5 >0 , y随x的增大而 ,
2.函数y=-3x+2,k=-3<0 , y随x的增大而 .
3.直线y=3x-5与直线y=3x+7的位置关系 .
4.直线y=2x-6与直线y=-x-6的位置关系 .
增大
减小
平行
相交
温故知新:
齐声朗读:
与y轴的交点是(0,-3)
与y轴的交点是(0,2)
直线 y=5x-3, b=-3
直线 y=-3x+2, b=2
5.一次函数的图像y=kx+b 与y轴的交点是( ),与x轴的交点是( , ).特别地,当b=0时,正比例函数y=kx与x轴, y轴的交点
都是( )即:正比例函数的图像是一条 的直线.
0, b
.
0,0
过原点
6. 满足函数关系式y=kx+b的x,y所对应的点(x,y)都在一次函数 y=kx+b的图象上;
反过来,一次函数y=kx+b的图象上的点(x,y)都满足关系式 y=kx+b.
即一次函数的表达式与图象是 的 .
一一对应
7、b值对一次函数图像位置的影响
当b>0时,点(0,b)位于 , ;
当b<0时,点(0,b)位于 , ;
当b=0 时,点(0,0)是 ,即正比例函数y=kx的图像是一定经过原点的一条直线.
y轴正半轴
在x轴的上方
y轴负半轴
在x轴的下方
原点
新课讲解
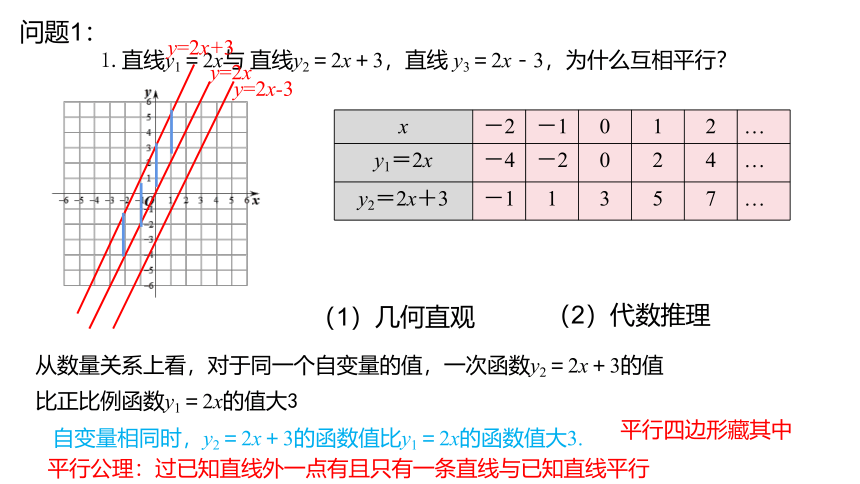
1.直线y1=2x与 直线y2=2x+3,直线 y3=2x-3,为什么互相平行?
x -2 -1 0 1 2 …
y1=2x -4 -2 0 2 4 …
y2=2x+3 -1 1 3 5 7 …
从数量关系上看,对于同一个自变量的值,一次函数y2=2x+3的值
比正比例函数y1=2x的值大3
自变量相同时,y2=2x+3的函数值比y1=2x的函数值大3.
问题1:
y=2x+3
y=2x
y=2x-3
(1)几何直观
(2)代数推理
平行公理:过已知直线外一点有且只有一条直线与已知直线平行
平行四边形藏其中
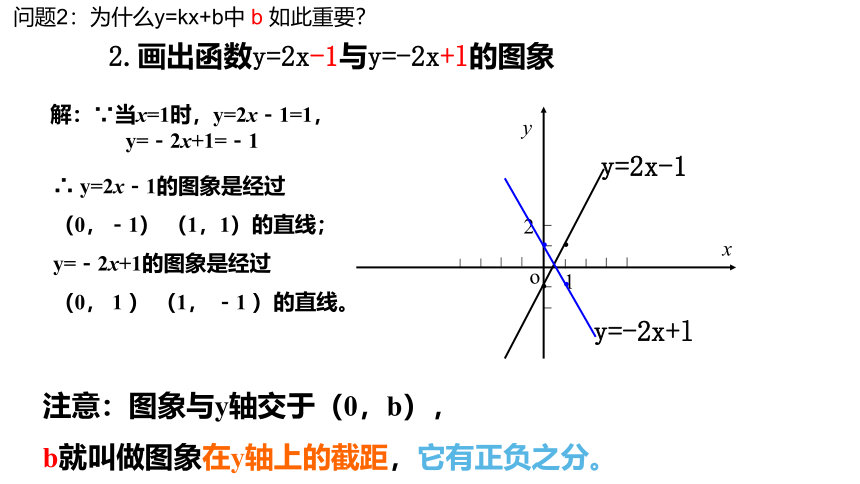
2.画出函数y=2x-1与y=-2x+l的图象
y
x
o
2
1
解:∵当x=1时,y=2x-1=1, y=-2x+1=-1
∴ y=2x-1的图象是经过
(0,-1) (1,1)的直线;
y=-2x+1的图象是经过
(0, 1 ) (1, -1 )的直线。
·
·
·
·
y=2x-1
y=-2x+l
注意:图象与y轴交于(0,b),
b就叫做图象在y轴上的截距,它有正负之分。
问题2:为什么y=kx+b中 b 如此重要?
新课讲解
y
1
2
3
4
-4
-3
-2
-1
x
1
2
3
4
-4
-3
-2
-1
O
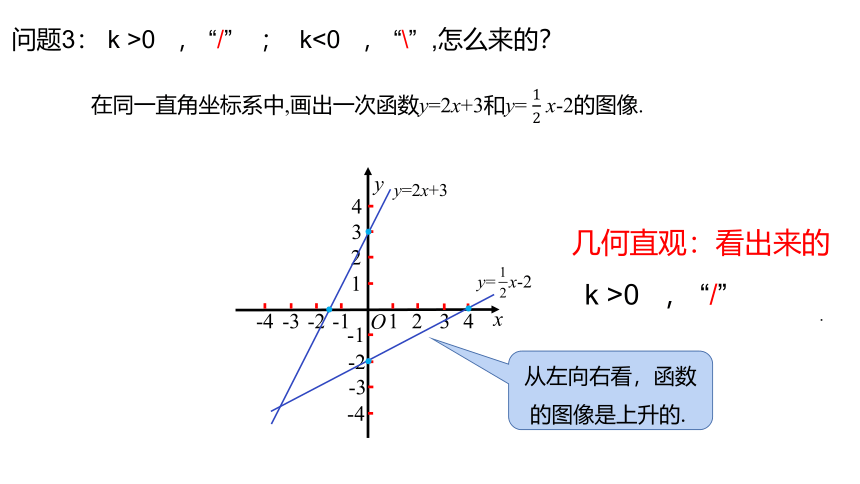
从左向右看,函数的图像是上升的.
y=2x+3
y= x-2
问题3: k >0 , “/” ; k<0 , “\” ,怎么来的?
在同一直角坐标系中,画出一次函数y=2x+3和y= x-2的图像.
.
k >0 , “/”
几何直观:看出来的
新课讲解
y
1
2
3
4
-4
-3
-2
-1
x
1
2
3
4
-4
-3
-2
-1
O
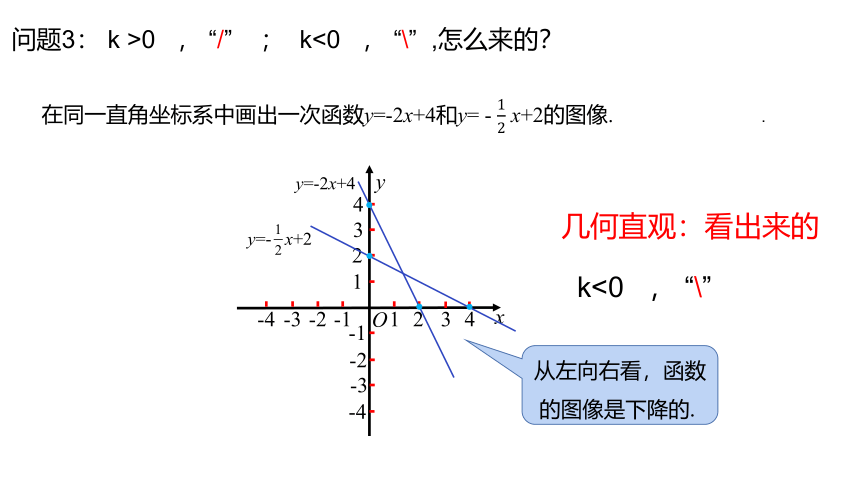
从左向右看,函数的图像是下降的.
y=-2x+4
y=- x+2
问题3: k >0 , “/” ; k<0 , “\” ,怎么来的?
在同一直角坐标系中画出一次函数y=-2x+4和y= - x+2的图像.
.
k<0 , “\”
几何直观:看出来的
对于一次函数y=kx+b(k,b为常数,且k≠0):
当k>0时,直线左低右高,y 的值随x 的值的增大而增大;
当k<0时,直线左高右低,y 的值随x 的值的增大而减小.
问题3: k >0 , “/” ; k<0 , “\” ,怎么来的?
k>0时,
数学语言:y随x的值的增大而增大;
符号语言:对于M(x1,y1),N(x2,y2)
当x1>x2时,y1>y2
当x1k<0时,
数学语言:y随x的值的增大而减小;
符号语言:对于M(x1,y1),N(x2,y2)
当x1>x2时,y1当x1y2.
文字语言:当k>0时,y随x的值的增大而增大;
符号语言:当k>0时,对于M(x1,y1),N(x2,y2),当x1>x2时,y1>y2
代数推理:
证明:当k>0时,对于M(x1,y1),N(x2,y2),
y1=kx1+b, y2=kx2+b
y1 > y2 , 点M在点N上方,y随x的值的增大而增大;
y1 - y2=(kx1+b) - (kx2+b)
=kx1+b - kx2 - b=k(x1 - x2)
当x1>x2时, x1 - x2>0,
k>0时,k(x1 - x2)>0
解:把y=kx+b向右平移 m(m>0)个单位,
x
y
0
问题4:
“左加右减”怎么来的?
一次函数y=kx+b向左m(m≥0)个单位长度后,得到的一次函数为y=k(x+m)+b;一次函数y=kx+b向右m(m≥0)个单位长度后得到的一次函数为y=k(x-m)+b.
平移后k不变,
设平移后的一次函数关系式为y=kx+
b
在原函数y=kx+b上取点A(0,b)
平移后对应点为 (m,b)
A
代入y=kx+ 得
b
b=km+
b
b
=-km+b
得平移后的一次函数关系式y=kx-km+b
得y=k(x-m)+b
A
A
规律总结:
简记为“左加右减,上加下减”
(左右平移只给x加减,
上下平移等号右边整体加减)
求证:无论m为何值时,函数 y = (m+1) x + 2m﹣6的图象都过某一定点.
解:由y = (m+1) x + 2m﹣6,得
y -x+6= (x+2)m.
令y -x+6=0 ,x+2=0.
解得 x=-2 ,y=-8.
所以,无论m为何值时,函数 y = (m+1) x + 2m﹣6的图象都过点(-2,-8).
问题5:特殊数量--------参数(字母系数)-----大胆猜想------特殊现象?
1. 已知点M(1,a)和点N(2,b)是一次函数y=-2x+1图像上的两点,则a与b的大小关系是( )
A. a >b B.a =b C. a<b D.以上都不对
A
新课讲解
方法一:
把x=1,2分别代入y=-2x+1,
得:a=-1,b=-3
∴ a>b
方法二:
∵y=-2x+1中k=-2<0
∴ y随x的增大而减小
又∵ 1<2
∴ a>b
当堂检测:
2.函数 y=kx-1的图象过定点 ;
3.若函数y=kx+b的图象过点(1 ,2),则k+b= .
(0,-1)
2
4.将直线y=-7x向左平移2个单位,可得到新的函数关系式为
y=-7x-14
5、把一次函数y=2x-1沿x轴向左平移1个单位,得到的直线解析式是
6.将直线y=-3x+1向右平移1个单位,可得到新的函数关系式为
7.把一次函数y=-2x+2沿x轴向右平移2个单位,得到的直线解析式是
y=2x+1
y=-3x+4
y=-2x+6
浙教版八上数学
第五章 一次函数 章末复习
数学是清楚的--------知识来龙去脉是清楚的
几何直观 + 代数推理-------完美融合
1.函数 y=5x-3,k=5 >0 , y随x的增大而 ,
2.函数y=-3x+2,k=-3<0 , y随x的增大而 .
3.直线y=3x-5与直线y=3x+7的位置关系 .
4.直线y=2x-6与直线y=-x-6的位置关系 .
增大
减小
平行
相交
温故知新:
齐声朗读:
与y轴的交点是(0,-3)
与y轴的交点是(0,2)
直线 y=5x-3, b=-3
直线 y=-3x+2, b=2
5.一次函数的图像y=kx+b 与y轴的交点是( ),与x轴的交点是( , ).特别地,当b=0时,正比例函数y=kx与x轴, y轴的交点
都是( )即:正比例函数的图像是一条 的直线.
0, b
.
0,0
过原点
6. 满足函数关系式y=kx+b的x,y所对应的点(x,y)都在一次函数 y=kx+b的图象上;
反过来,一次函数y=kx+b的图象上的点(x,y)都满足关系式 y=kx+b.
即一次函数的表达式与图象是 的 .
一一对应
7、b值对一次函数图像位置的影响
当b>0时,点(0,b)位于 , ;
当b<0时,点(0,b)位于 , ;
当b=0 时,点(0,0)是 ,即正比例函数y=kx的图像是一定经过原点的一条直线.
y轴正半轴
在x轴的上方
y轴负半轴
在x轴的下方
原点
新课讲解
1.直线y1=2x与 直线y2=2x+3,直线 y3=2x-3,为什么互相平行?
x -2 -1 0 1 2 …
y1=2x -4 -2 0 2 4 …
y2=2x+3 -1 1 3 5 7 …
从数量关系上看,对于同一个自变量的值,一次函数y2=2x+3的值
比正比例函数y1=2x的值大3
自变量相同时,y2=2x+3的函数值比y1=2x的函数值大3.
问题1:
y=2x+3
y=2x
y=2x-3
(1)几何直观
(2)代数推理
平行公理:过已知直线外一点有且只有一条直线与已知直线平行
平行四边形藏其中
2.画出函数y=2x-1与y=-2x+l的图象
y
x
o
2
1
解:∵当x=1时,y=2x-1=1, y=-2x+1=-1
∴ y=2x-1的图象是经过
(0,-1) (1,1)的直线;
y=-2x+1的图象是经过
(0, 1 ) (1, -1 )的直线。
·
·
·
·
y=2x-1
y=-2x+l
注意:图象与y轴交于(0,b),
b就叫做图象在y轴上的截距,它有正负之分。
问题2:为什么y=kx+b中 b 如此重要?
新课讲解
y
1
2
3
4
-4
-3
-2
-1
x
1
2
3
4
-4
-3
-2
-1
O
从左向右看,函数的图像是上升的.
y=2x+3
y= x-2
问题3: k >0 , “/” ; k<0 , “\” ,怎么来的?
在同一直角坐标系中,画出一次函数y=2x+3和y= x-2的图像.
.
k >0 , “/”
几何直观:看出来的
新课讲解
y
1
2
3
4
-4
-3
-2
-1
x
1
2
3
4
-4
-3
-2
-1
O
从左向右看,函数的图像是下降的.
y=-2x+4
y=- x+2
问题3: k >0 , “/” ; k<0 , “\” ,怎么来的?
在同一直角坐标系中画出一次函数y=-2x+4和y= - x+2的图像.
.
k<0 , “\”
几何直观:看出来的
对于一次函数y=kx+b(k,b为常数,且k≠0):
当k>0时,直线左低右高,y 的值随x 的值的增大而增大;
当k<0时,直线左高右低,y 的值随x 的值的增大而减小.
问题3: k >0 , “/” ; k<0 , “\” ,怎么来的?
k>0时,
数学语言:y随x的值的增大而增大;
符号语言:对于M(x1,y1),N(x2,y2)
当x1>x2时,y1>y2
当x1
数学语言:y随x的值的增大而减小;
符号语言:对于M(x1,y1),N(x2,y2)
当x1>x2时,y1
文字语言:当k>0时,y随x的值的增大而增大;
符号语言:当k>0时,对于M(x1,y1),N(x2,y2),当x1>x2时,y1>y2
代数推理:
证明:当k>0时,对于M(x1,y1),N(x2,y2),
y1=kx1+b, y2=kx2+b
y1 > y2 , 点M在点N上方,y随x的值的增大而增大;
y1 - y2=(kx1+b) - (kx2+b)
=kx1+b - kx2 - b=k(x1 - x2)
当x1>x2时, x1 - x2>0,
k>0时,k(x1 - x2)>0
解:把y=kx+b向右平移 m(m>0)个单位,
x
y
0
问题4:
“左加右减”怎么来的?
一次函数y=kx+b向左m(m≥0)个单位长度后,得到的一次函数为y=k(x+m)+b;一次函数y=kx+b向右m(m≥0)个单位长度后得到的一次函数为y=k(x-m)+b.
平移后k不变,
设平移后的一次函数关系式为y=kx+
b
在原函数y=kx+b上取点A(0,b)
平移后对应点为 (m,b)
A
代入y=kx+ 得
b
b=km+
b
b
=-km+b
得平移后的一次函数关系式y=kx-km+b
得y=k(x-m)+b
A
A
规律总结:
简记为“左加右减,上加下减”
(左右平移只给x加减,
上下平移等号右边整体加减)
求证:无论m为何值时,函数 y = (m+1) x + 2m﹣6的图象都过某一定点.
解:由y = (m+1) x + 2m﹣6,得
y -x+6= (x+2)m.
令y -x+6=0 ,x+2=0.
解得 x=-2 ,y=-8.
所以,无论m为何值时,函数 y = (m+1) x + 2m﹣6的图象都过点(-2,-8).
问题5:特殊数量--------参数(字母系数)-----大胆猜想------特殊现象?
1. 已知点M(1,a)和点N(2,b)是一次函数y=-2x+1图像上的两点,则a与b的大小关系是( )
A. a >b B.a =b C. a<b D.以上都不对
A
新课讲解
方法一:
把x=1,2分别代入y=-2x+1,
得:a=-1,b=-3
∴ a>b
方法二:
∵y=-2x+1中k=-2<0
∴ y随x的增大而减小
又∵ 1<2
∴ a>b
当堂检测:
2.函数 y=kx-1的图象过定点 ;
3.若函数y=kx+b的图象过点(1 ,2),则k+b= .
(0,-1)
2
4.将直线y=-7x向左平移2个单位,可得到新的函数关系式为
y=-7x-14
5、把一次函数y=2x-1沿x轴向左平移1个单位,得到的直线解析式是
6.将直线y=-3x+1向右平移1个单位,可得到新的函数关系式为
7.把一次函数y=-2x+2沿x轴向右平移2个单位,得到的直线解析式是
y=2x+1
y=-3x+4
y=-2x+6
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
