第三章圆的基本性质教案[上学期]
图片预览



文档简介
第8周第1课时上课时间10月16日(星期一)本学期累计教案28个
课题:3.1圆 (1)
教学目标:
1、经历形成圆的概念的过程,经历探索点与圆的位置关系得过程。
2、理解圆的概念,了解点与圆的位置关系;
3、会在简单条件下判断点与圆的位置关系。
教学重点:圆、弦和弧的概念,弧的表示法和点与圆的位置关系。
教学难点:点与圆的位置关系
教学过程:
一、创设情景,引入新课
1、在小学我们已经学过一些圆的知识,并且知道圆不仅在几何中占有极其重要的地位,而且在日常生活和生产实践中有着广泛的应用,你能举例说明我们周围那些物体是圆形的吗?
在学生回答的基础上,教师总结:实际生活中圆形物体的例子很多(出示一些投影图象)
2、提问:人们为什么把车轮做成圆形的?
在学生回答的基础上,教师指出:这是因为圆具有一些特殊的性质,在这一章里我们将系统研究:什么是圆?圆有哪些性质?
二、描述圆的发生过程,给出圆的定义和有关概念
1、如何用圆规画出一个圆?
2、要在操场上画一个半径为5米的大圆,如何画呢?
3、从实践中给出圆的定义
在同一平面内线段OP绕它的一个端点O旋转一周,另一个端点P所经过的封闭曲线叫做圆,定点O叫做圆心,定长 OP叫做半径。
以点0为圆心的圆记作⊙O,读作“圆O”
(利用几何画板动态演示)
4、圆的有关概念
1)连结圆上任意两点的线段叫做弦,如图BC.经过圆心的弦是直径,
图中的AB。直径等于半径的2倍.
(2)圆上任意两点间的部分叫做圆弧,简称弧.弧用符号“⌒”表示.
小于半圆的弧叫做劣弧,如图中以B、C为端点的劣弧记做“⌒BC”;
大于半圆的弧叫做优弧,优弧要用三个字母表示,如图中的.
(3)半径相等的两个圆能够完全重合,我们把半径相等的两个圆叫做
等圆.例如,图中的⊙O1和⊙O2是等圆.
圆心相同,半径不相等的圆叫做同心圆。(学生画同心圆)
5、完成课本第58页的做一做
三、点和圆的位置关系
同学们看过奥运会的射击比赛吗?射击的靶子是由许多圆组成的,射击的成绩是由击中靶子不同位置所决定的;右图是一位运动员射击10发子弹在靶上留下的痕迹。你知道这个运动员的成绩吗?请同学们算一算。(击中最里面的圆的成绩为10环,依次为9、8、…、1环)
这一现象体现了平面上的点与圆的位置关系,如何判断点与圆的位置关系呢?我们知道圆上的所有点到圆心的距离都等于半径,若点在圆上,那么这个点到圆心的距离等于半径,若点在圆外,那么这个点到圆心的距离大于半径,若点在圆内,那么这个点到圆心的距离小于半径。
如图,设⊙O的半径为r,A点在圆内,B点在圆上,C点在圆外,那
OA<r, OB=r, OC>r.反过来也成立,即
若点A在⊙O内
若点A在⊙O上
若点A在⊙O外
思考与练习
(1)课内练习第2题
(2)例题:例1 如图所示,在A地正北80m的B处有一幢民房,正西100m的C处有一变电设施,在BC的中点D处是一古建筑。因施工需要,必须在A处进行一次爆破。为使民房、变电设施、古建筑都不遭到破坏,问爆破影响面的半径应控制在什么范围内?
(3)如图,在A岛附近,半径约250km的范围内是一暗礁区,往北300km有一灯塔B,往西400km有一灯塔C。现有一渔船沿CB航行,问渔船会进入暗礁区吗?(课本第60页第6题)
四、课堂小结:
这节课学习了那些内容?
1、圆的定义和有关概念
2、点和圆的位置关系
五、作业
见作业本
第8周第2课时上课时间10月17日(星期二)本学期累计教案29个
课题:3.1圆(2)
教学目标:
知识目标:
1、通过问题的解决过程,使学生明确三角形的外接圆、三角形的外心、圆的内接三角形的概念,理解“不在同一直线上的三点确定一个圆”。
2、使学生能熟练掌握应用尺规“过不在同一直线上三点作圆”的方法。
3、向学生渗透转化、分类讨论等数学思想方法,为今后继续进一步学习数学打下基础。
能力目标:
1、通过学生自己动手作图,在动手参与的过程中探索、发现科学知识,进一步提高学生动手做的积极性。
2、提高学生应用数学知识解决生活中实际问题的能力。
情感目标:
1、增强学生的数学应用意识,提高学生学习数学的兴趣和积极性。
2、培养学生树立良好的创新意识、养成永无止境的科学探索精神。
教学重点:过不在一直线上的三点作圆的方法
教学难点:如何确定圆的思维过程
教学过程:
一:创设情境、提出问题
投影片出示问题:(破镜重圆)
现有一块打碎的圆形玻璃镜子残片,想重新去玻璃店配一块同样大小的圆形玻璃镜子,请问怎样去配制呢?
思考:如何解决这一实际问题?下面我们共同探寻解决这一问题的办法
二、实践活动,探究新知
探究①:过一个已知点A能否作圆?如果能,可以作几个? (让学生动手去完成)
学生讨论并发现:过点A所作圆的圆心在哪儿(圆心不定)?半径多大(半径不定)?可以作几个这样的圆(无数个)?
探究②:过已知两点A、B能否作圆?如果能,可以作几个? 圆心在哪里?(学生动手去完成)
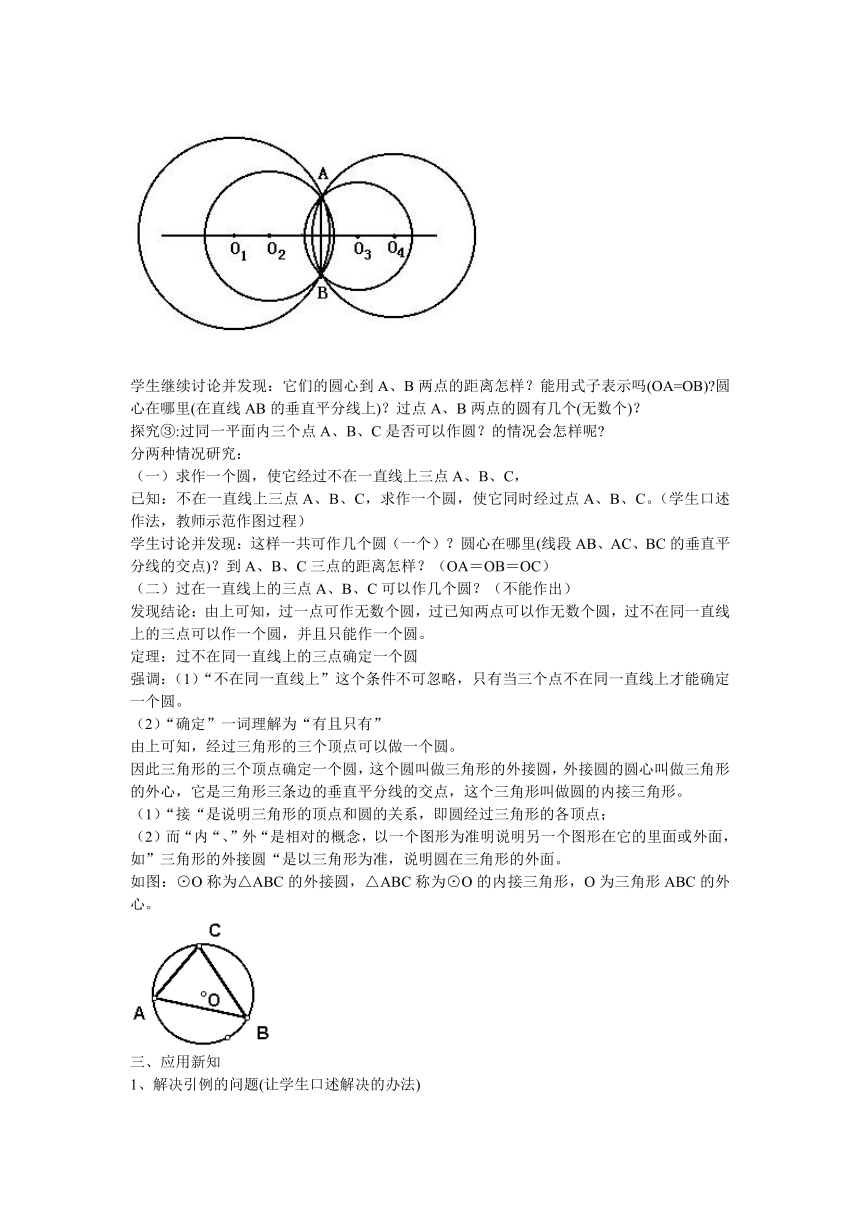
学生继续讨论并发现:它们的圆心到A、B两点的距离怎样?能用式子表示吗(OA=OB) 圆心在哪里(在直线AB的垂直平分线上)?过点A、B两点的圆有几个(无数个)?
探究③:过同一平面内三个点A、B、C是否可以作圆?的情况会怎样呢
分两种情况研究:
(一)求作一个圆,使它经过不在一直线上三点A、B、C,
已知:不在一直线上三点A、B、C,求作一个圆,使它同时经过点A、B、C。(学生口述作法,教师示范作图过程)
学生讨论并发现:这样一共可作几个圆(一个)?圆心在哪里(线段AB、AC、BC的垂直平分线的交点)?到A、B、C三点的距离怎样?(OA=OB=OC)
(二)过在一直线上的三点A、B、C可以作几个圆?(不能作出)
发现结论:由上可知,过一点可作无数个圆,过已知两点可以作无数个圆,过不在同一直线上的三点可以作一个圆,并且只能作一个圆。
定理:过不在同一直线上的三点确定一个圆
强调:(1)“不在同一直线上”这个条件不可忽略,只有当三个点不在同一直线上才能确定一个圆。
(2)“确定”一词理解为“有且只有”
由上可知,经过三角形的三个顶点可以做一个圆。
因此三角形的三个顶点确定一个圆,这个圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,它是三角形三条边的垂直平分线的交点,这个三角形叫做圆的内接三角形。
(1)“接“是说明三角形的顶点和圆的关系,即圆经过三角形的各顶点;
(2)而“内“、”外“是相对的概念,以一个图形为准明说明另一个图形在它的里面或外面,如”三角形的外接圆“是以三角形为准,说明圆在三角形的外面。
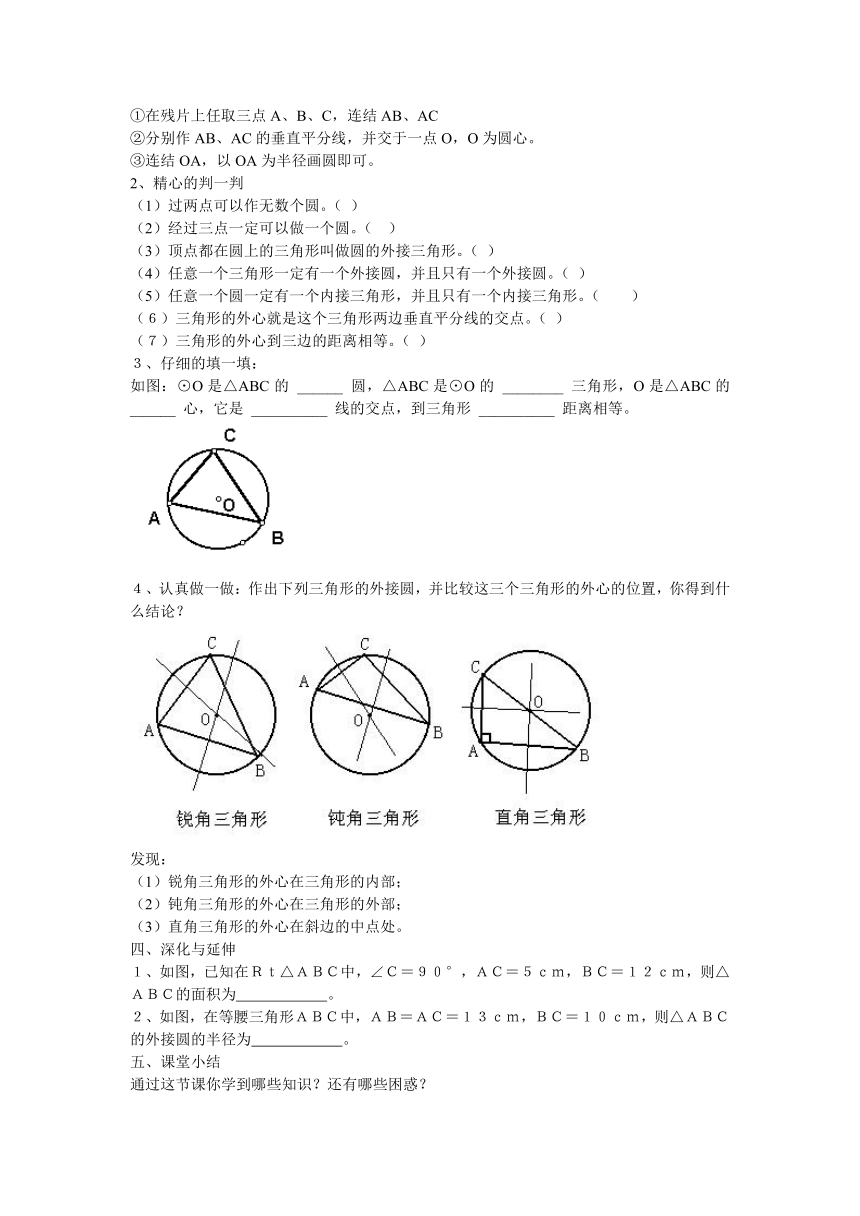
如图:⊙O称为△ABC的外接圆,△ABC称为⊙O的内接三角形,O为三角形ABC的外心。
三、应用新知
1、解决引例的问题(让学生口述解决的办法)
①在残片上任取三点A、B、C,连结AB、AC
②分别作AB、AC的垂直平分线,并交于一点O,O为圆心。
③连结OA,以OA为半径画圆即可。
2、精心的判一判
(1)过两点可以作无数个圆。( )
(2)经过三点一定可以做一个圆。( )
(3)顶点都在圆上的三角形叫做圆的外接三角形。( )
(4)任意一个三角形一定有一个外接圆,并且只有一个外接圆。( )
(5)任意一个圆一定有一个内接三角形,并且只有一个内接三角形。( )
(6)三角形的外心就是这个三角形两边垂直平分线的交点。( )
(7)三角形的外心到三边的距离相等。( )
3、仔细的填一填:
如图:⊙O是△ABC的 ______ 圆,△ABC是⊙O的 ________ 三角形,O是△ABC的 ______ 心,它是 __________ 线的交点,到三角形 __________ 距离相等。
4、认真做一做:作出下列三角形的外接圆,并比较这三个三角形的外心的位置,你得到什么结论?
发现:
(1)锐角三角形的外心在三角形的内部;
(2)钝角三角形的外心在三角形的外部;
(3)直角三角形的外心在斜边的中点处。
四、深化与延伸
1、如图,已知在Rt△ABC中,∠C=90°,AC=5cm,BC=12cm,则△ABC的面积为 。
2、如图,在等腰三角形ABC中,AB=AC=13cm,BC=10cm,则△ABC的外接圆的半径为 。
五、课堂小结
通过这节课你学到哪些知识?还有哪些困惑?
六、作业:
1、作业本
2、动手做一做
(1) 怎样找出一个圆形纸片的圆心?(请你想出尽可能多的方法)
(2)过四个点能否作一个圆
第8周第3课时上课时间10月18日(星期三)本学期累计教案30个
课题:3.2圆的轴对称性(1)
教学目标
1.使学生理解圆的轴对称性.
2.掌握垂径定理.
3.学会运用垂径定理解决有关弦、弧、弦心距以及半径之间的证明和计算问题.
教学重点
垂径定理是圆的轴对称性的重要体现,是今后解决有关计算、证明和作图问题的重要依据,它有着广泛的应用,因此,本节课的教学重点是:垂径定理及其应用.
教学难点
垂径定理的推导利用了圆的轴对称性,它是一种运动变换,这种证明方法学生不常用到,与严格的逻辑推理比较,在证明的表述上学生会发生困难,因此垂径定理的推导是本节课的难点.
教学关键
理解圆的轴对称性.
教学环节的设计
这节课我通过七个环节来完成本节课的教学目标,它们是:
复习提问,创设情境;引入新课,揭示课题;讲解新课,探求新知;应用新知,体验成功;
目标训练,及时反馈;总结回顾,反思内化;布置作业,巩固新知.
一、复习提问,创设情境
1.教师演示:将一等腰三角形沿着底边上的高对折,启发学生共同回忆等腰三角形是轴对称图形,同时复习轴对称图形的概念;
2.提出问题:如果以这个等腰三角形的顶点为圆心,腰长为半径作圆,得到的圆是否是轴对称图形呢?(教师用教具演示,学生自己操作)
二、引入新课,揭示课题
1.在第一个环节的基础上,引导学生归纳得出结论:
圆是轴对称图形,每一条直径所在的直线都是对称轴.
强调:
(1)对称轴是直线,不能说每一条直径都是它的对称轴;
(2)圆的对称轴有无数条.
判断:任意一条直径都是圆的对称轴( )
设计意图:让学生更好的理解圆的轴对称轴新性,为下一环节探究新知作好准备.
三、讲解新课,探求新知
先按课本进行合作学习
1.任意作一个圆和这个圆的任意一条直径CD;
2.作一条和直径CD的垂线的弦,AB与CD相交于点E.
提出问题:把圆沿着直径CD所在的直线对折,你发现哪些点、线段、圆弧重合?
在学生探索的基础上,得出结论:(先介绍弧相等的概念)
①EA=EB;② AC=BC,AD=BD.
理由如下:∵∠OEA=∠OEB=Rt∠,根据圆的轴轴对称性,可得射线EA与EB重合,
∴点A与点B重合,弧AC和弧BC重合,弧AD和弧BD重合.
∴ EA=EB, AC=BC,AD=BD.
思考:你能利用等腰三角形的性质,说明OA平分CD吗?(课内练习1)
注:老教材这个内容放在圆心角、圆周角之后,垂径定理完全可以不用圆的轴对称性来证,可用等腰三角形的性质来证明,现在只能证前面一个(略).
然后把此结论归纳成命题的形式:
垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧.
垂径定理的几何语言
∵CD为直径,CD⊥AB(OC⊥AB)
∴ EA=EB, AC=BC,AD=BD.
四、应用新知,体验成功
例1 已知AB,如图,用直尺和圆规求作这条弧的中点.(先介绍弧中点概念)
作法:
⒈连结AB.
⒉作AB的垂直平分线 CD, 交弧AB于点E.
点E就是所求弧AB的中点.
变式一: 求弧AB的四等分点.
思路:先将弧AB平分,再用同样方法将弧AE、弧BE平分.
(图略)
有一位同学这样画,错在哪里?
1.作AB的垂直平分线CD
2.作AT、BT的垂直平分线EF、GH(图略)
教师强调:等分弧时一定要作弧所对的弦的垂直平分线.
变式二:你能确定弧AB的圆心吗?
方法:只要在圆弧上任意取三点,得到三条弦,画其中两条弦的垂直平分线,交点即为圆弧的圆心.
例2 一条排水管的截面如图所示.排水管的半径OB=10,水面宽AB=16,求截面圆心O到水面的距离OC .
思路:
先作出圆心O到水面的距离OC,即画 OC⊥AB,∴AC=BC=8,
在Rt△OCB中,
∴圆心O到水面的距离OC为6.
例3 已知:如图,线段AB与⊙O交于C、D两点,且OA=OB .求证:AC=BD .
思路:
作OM⊥AB,垂足为M, ∴CM=DM
∵OA=OB , ∴AM=BM , ∴AC=BD.
概念:圆心到圆的一条弦的距离叫做弦心距.
小结:
1.画弦心距是圆中常见的辅助线;
2.半径(r)、半弦、弦心距(d)组成的直角三角形是研究与圆有关问题的主要思路,它们之间的关系:弦长.
注:弦长、半径、弦心距三个量中已知两个,就可以求出第三个.
五、目标训练,及时反馈
1.已知⊙0的半径为13,一条弦的AB的弦心距为5,则这条弦的弦长等于 .
答案:24
2.如图,AB是⊙0的中直径,CD为弦,CD⊥AB于E,则下列结论中不一定成立的是( )
A.∠COE=∠DOE B.CE=DE C.OE=BE D.BD=BC
答案:C
3.过⊙O内一点M的最长弦长为10cm,最短弦长为8cm,那么OM长为( )
A.3 B.6cm C. cm D.9cm
答案:A
注:圆内过定点M的弦中,最长的弦是过定点M的直径,最短的弦是过定点M与OM垂直的弦,此结论最好让学生记住,课本作业题也有类似的题目.
4.如图,⊙O的直径为10,弦AB长为8,M是弦AB上的动点,则OM的长的取值范围是( )
A.3≤OM≤5 B.4≤OM≤5 C.3答案:A
5. 已知⊙O的半径为10,弦AB∥CD,AB=12,CD=16,则AB和CD的距离为 .
答案:2或24
注:要分两种情况讨论:(1)弦AB、CD在圆心O的两侧;(2)弦AB、CD在圆心O的同侧.
6.如图,已知AB、AC为弦,OM⊥AB于点M, ON⊥AC于点N ,BC=4,求MN的长.
思路:由垂径定理可得M、N分别是AB、AC的中点,
所以MN=BC=2.
六、总结回顾,反思内化
师生共同总结:
1.本节课主要内容:(1)圆的轴对称性;(2)垂径定理.
2.垂径定理的应用:(1)作图;(2)计算和证明.
3.解题的主要方法:
(1)画弦心距是圆中常见的辅助线;
(2)半径(r)、半弦、弦心距(d)组成的直角三角形是研究与圆有关问题的主要思路,它们之间的关系:弦长.
七、布置作业, 巩固新知
P75作业题1~6,第7题选做.
第8周第4课时上课时间10月19日(星期四)本学期累计教案31个
课题:3.2圆的轴对称性(2)
教学目标
1.使学生掌握垂径定理及其推论,并会用垂径定理及其推论解决有关证明、计算和作图问题;
2.使学生了解垂径定理及其推论在实际中的应用,培养学生把实际问题转化为数学问题的能力和计算能力,结合应用问题向学生进行爱国主义教育.
教学重点和难点
垂径定理的两个推论是重点;由定理推出推论1是难点.
教学过程设计
一、从学生原有的认知结构提出问题
1.画图叙述垂径定理,并说出定理的题设和结论.(由学生叙述)
2.结合图形7-35,教师引导学生写出垂径定理的下述形式:
题设 结论
线CD平分弦AB
指出:垂径定理是由两个条件推出三个结论,即由①②推出③④⑤.
提问:如果把题设和结论中的5条适当互换,情况又会怎样呢 引出垂径定理推论的课题
. 二、运用逆向思维方法探讨垂径定理的推论
1.引导学生观察图形,选①③为题设,可得:
由于一个圆的任意两条直径总是互相平分的,但是它们不一定是互相垂直的,所以要使上面的题设能够推出上面的结论,还必须加上“弦AB不是直径”这一条件.
这个命题是否为真命题,需要证明,结合图形请同学叙述已知、求证,教师在黑板上写出.
已知:如图7-36,在⊙O中,直径CD与弦AB(不是直径)相交于E,且E是AB的中点.
求证:CD⊥AB,.
分析:要证明CD⊥AB,即证OE⊥AB,而E是AB的中点,即证OE为AB的中垂线.由等腰三角形的性质可证之.利用垂径定理可知AC=BC,AD=BD.
证明:连结OA,OB,则OA=OB,△AOB为等腰三角形.
因为E是AB中点,所以OE⊥AB,即CD⊥AB,
又因为CD是直径,所以
2. 若选①④为题设,可得:
以上命题用投影打出,引导学生自己证出?
3.根据上面具体的分析,在感性认识的基础上,引导学生用文字叙述其中最常用的二个命题,教师板书出垂径定理的推论1.
推论1 (1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;
(2) 平分弦所对的一条弧的直径,垂直平分弦并且平分弦所对的另一条弧.
三、应用举例,变式练习
例1 平分已知.
引导学生画图,写已知、求作.
已知: (图7-38),求作:的中点.
分析:弦的垂直平分线经过圆心,并且平分弦所对的两条弧.因此,连结AB,作弦AB的垂直平分线,它一定平分.
作法:(由学生口述,教师板书,师生共同作图)
练习1 四等分已知.
引导学生在平分的基础上,进一步平分AM和BM,即可四等分AB.
作图后,提问:四等分弦AB是否可四等分,为什么 如图7-39所示.
在学生回答的基础上,强调:这种作法是错误的,虽然在等分时作法是对的,但是在等分和时是错误的,因为AT,BT不是和所对的弦.因此AT,BT的垂直平分线不能平分和,请同学们务必注意.
练习2 按图7-40,填空:在⊙O中
(1)若MN⊥AB,MN为直径;则 , , ;
(2)若AC=BC,MN为直径;AB不是直径,则 , , ;
(3)若MN⊥AB,AC=BC,则 , , ;
(4)若=,MN为直径,则 , , .
此练习的目的是为了帮助学生掌握垂径定理及推论1的条件和结论.
例2 1300多年前,我国隋代建造的赵州石拱桥(图7-41)的桥拱是圆弧形,它的跨度(弧
所对的弦的长)为37.4米,拱高(弧的中点到弧的距离,也叫弓形高)为7.2米,求桥拱的半径.(精确到0.1米)
首先可借此题向学生介绍“赵州桥”,对学生进行爱国主义教育,同
时也可激发学生学习数学的兴趣.
关于赵州桥的说明:
赵州桥又名“安济桥”,位于河北省赵县城南交河上,是我国现存的著名古代大石拱桥、
?隋开皇大业年间(590~608)由李春创建.桥单孔,全长50.82米,桥面宽约10米,跨径约
为37米,弧形平缓,拱圈为28条并列的石条组成,上设四个小拱,既减轻重量,节省材料,
又便于排洪,且增美观?在世界桥梁史上,其设计与工艺之新为石拱桥的卓越典范,跨度之
大在当时亦属首创,反映了我国古代劳动人民的智慧与才能.
分析:(1)首先说明跨度、拱高等概念,然后引导学生设法把实际问题转化为数学问题
,并画出几何图形(图7-42),且一边画图一边解释:桥拱是圆弧形,以O为圆心,R为半径画
出一段圆弧表示桥拱,弦AB表示桥的跨度,即AB=37.4米,的中点C到线段AB的距离为7
.2米.
这样我们就可以根据实际问题,参照上图写出数学问题的已知和求解.
(2)实际问题已转化为数学问题,下面讨论如何解决这个问题.
启发学生观察图形、发现:对于,如果经过圆心O作弦AB的垂线OD,D为垂足,并延长交于点C,那么根据垂径定理可知,OD平分弦,OC平分弧,即C点为AB的中点,CD就是
拱高,这样做出的图形符合题意.
根据勾股定理,在Rt△AOD中就可求出半径R. 解题过程,参考课本. 对于此题,学生往往是过的中点C先作出弓形高CD,即过C作CD⊥AB,垂足为D,如果是这样的话,可引导学生根据垂径定理,首先证明直线CD经过圆心O,仍然可利用勾股定理,求出半径R.
说明:此题的解题思路是,经过圆心作弦的垂线,说明它平分弦且平分弦所对的弧?也
可以经过弧的中点作弦的垂线,说明它平分弦且经过圆心.解决这类问题时,只要抓住弦长
、弦心距、弓形高及半径之间的关系,已知其中的两个量,可以求出其它两个未知量,这种
思考方法今后要经常用到.
例3 已知;如图7-43,⊙O半径为6厘米,弦AB与半径OA的夹角为30°.
求:弦AB的长.
分析:已知圆的半径和半径与弦的夹角.要求弦长,只要利用圆的半径、弦长、圆心到
弦的距离之间的关系即可.过圆心O作AB的垂线段OD,解Rt△AOD,求出AD即可求得AB.
解:作OD⊥AB于D,则AD=DB,
在Rt△AOD中,因为∠DAO=30°
练习3 如图7-44(厘米)
在直径为650毫米的圆柱形油槽内装入一些油后,截面如图所示.若油面宽AB=600毫米,求油的最大深度.
通过此练习题,进一步培养学生把实际问题转化为数学问题的能力.再一次明确弦长a、弦心距d、半径r及弓形高h之间的关系.(图7-45)
四、师生共同小结
问:这节课我们学习了哪些主要内容
在学生回答的基础上,用投影出示垂径定理及其推论的基本图形,如图7-46.
指出:若垂径定理或推论中的某一个成立,则
(1) △CAB,△OAB,△DAB都是等腰三角形,弦AB是它们公共的底边,直径CD是它
们的顶角平分线和底边的垂直平分线.
(2) △ACD和△BCD是全等的直角三角形,直径CD是它们公共的斜边,AE,BE分别是斜边
(2)上的高,AO,BO分别是斜边上的中线?在这两个三角形中可以运用直角三角形的一系列性质.
(3
通过应用题的学习,培养把实际问题抽象成数学问题的意识,从而提高转化能力和计算能力.
六、布置作业:见作业本
第8周第5-6课时上课时间10月20日(星期五)本学期累计教案33个
课题:3.1——3.2 练习课(见实验检测六)
第9周第1课时上课时间10月23日(星期一)本学期累计教案34个
课题:3.3圆心角(1)
教学目标:1、经历探索圆的中心对称性和旋转不变性的过程,
2、理解圆心角的概念,并掌握“在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦相等”的定理(圆心角定理)。
3、体验利用旋转变换来研究圆的性质的思想方法。
教学重点:圆心角定理
教学难点:根据圆的旋转不变性推出圆心角定理,需用到图形的旋转变换。
教学内容设计
(一)圆的对称性和旋转不变性
学生动手画圆,对折、观察得出:圆是轴对称图形和中心对称图形;圆的旋转不变性.
引出圆心角和弦心距的概念:
圆心角定义:顶点在圆心的角叫圆心角.
弦心距定义:从圆心到弦的距离叫做弦心距.
(二)圆心角、弧、弦、弦心距之间的关系
应用电脑动画(实验)观察,在同圆等圆中,圆心角变化时,圆心角所对应的弧、弦、弦心距之间的关系,得出定理的内容.这样既培养学生观察、比较、分析和归纳知识的能力,又可以充分调动学生的学习的积极性.
定理:在同圆等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对弦的弦心距也相等.
(三)应用、巩固和反思 ( http: / / www.teachercn.com / Xxyw / Fs / " \t "_blank )
1、判断题,下列说法正确吗?为什么?
如图,因为∠AOB=∠COD,所以AB= CD, =.
2、例1、用直尺和圆规把⊙O四等分
(可以让学生先尝试自己找出作法,在学生尝试过程中,教师作适当的启发)
提问:如何把圆八等分
(四)深化提高,得出推论
先让学生观察右图,提问:圆周所对的圆心角有多大?(360°)请大家想象一下,当把顶点在圆心的圆周等分成360份后,相应的把整个圆分成多少份?(360份)这时,每一份圆心角即1°的圆心角就对着1°的弧,我们把这一份的弧叫做1°的弧。
提问:n°的圆心角所对的弧是几度?
推论:圆心角的度数等于它所对的弧的度数。
练习:(1)你还有什么方法把圆八等分?
(2)课本第70页课内练习1、2、3
(六)小结:学生自己归纳,老师指导.
知识:①圆的对称性和旋转不变性;②圆心角、弧、弦、弦心距之间关系,它反映出在圆中相等量的灵活转换.
能力和方法:①增加了证明角相等、线段相等以及弧相等的新方法;②实验、观察、发现新问题,探究和解决问题的能力.
(七)作业:
(1)课本第71页作业题 和作业本
(2)圆心角定理是在同圆和等圆这个大前提下,已知圆心角相等,得出其余的三组量相等,请同学们课后思考,在这个大前提下,把圆心角相等与结论中的任何一个交换位置,可以得到新命题,这三个是真命题吗?如何证明?
第9周第2课时上课时间10月24日(星期二)本学期累计教案35个
课题:3.3圆心角(2)
教学目标:
1. 经历探索圆心角定理的逆定理的过程;
2. 掌握”在同圆或等圆中,如果两个圆心角、两条弧、两条弦,两个圆心距中有一对量相等,那么它们所对应的其余各对量都相等”这个圆的性质;
3. 会运用关于圆心角,弧,弦,弦心距之间相互关系的定理解决简单的几何问题..
教学重点与难点:
教学重点: 关于圆心角,弧,弦,弦心距之间相互关系的性质
教学难点:例2(1)题,例3涉及四边形,圆等较多知识点,且思路不易形成,是本节的教学难点
教学过程:
1. 复习旧知,创设情景:
1. 圆具有哪些性质
2. 如图,已知:⊙O上有两点A、B,连结OA、OB,作∠AOB的角平分线交⊙O于点C,连结AC、BC.图中有哪些量是相等的
复习圆心角定理的内容.
3. 请写出圆心角定理的逆命题,并证明它们的正确性.
(1).逆命题 : 在同圆或等圆中,相等的弧所对的圆心角相等,所对的弦相等,所对的弦的弦心距相等。
(2) 逆命题 : 在同圆或等圆中,相等的弦所对的圆心角相等,所对的弧相等,弦的弦心距相等。
(3)逆命题 : 在同圆或等圆中,相等的弦心距对应弦相等,弦所对的圆心角相等,所对的弧相等。
结合图形说出已知和求证并给出简要的证明过程
由此引出新课.
2. 新课讲解
1、运用上面的结论来解决下面的问题:
已知:如图,AB、CD是⊙O的两条弦,OE、OF为AB、CD的弦心距,根据本节定理及推论填空:
(1)如果AB=CD,那么
_____________,________,____________。
(2)如果OE=OF,那么
_____________,________,____________。
(3)如果弧AB=弧CD 那么
______________,__________,____________。
(4)如果∠AOB=∠COD,那么
_________,________,_________。
2、上面的练习说明:
以下的四个量中只要有一个量相等,就可以得到
其余的量相等:
⑴∠AOB=∠COD⑵AB=CD
⑶OE=OF⑷弧AB=弧CD
3、一般地,圆有下面的性质
在同圆或等圆中,如果两个圆心角、两条弧、两条弦、两个弦心距中有一组量相等,那么它们所对应的其余的各组量都相等。
4.例题讲解:
例2:如图,等边三角形ABC内接于⊙O,连结OA,OB,OC.
⑴ ∠AOB 、∠COB、 ∠AOC分别为多少度?
⑵延长AO,分别交BC于点P,弧BC于点D,连结BD,CD.判断三角形OBD是哪一种特殊三角形?
⑶判断四边形BDCO是哪一种特殊四边形,并说明理由。
⑷若⊙O的半径为r,求等边ABC三角形的边长?
⑸若等边三角形ABC的边长r,求⊙O的半径为 多少?
当r = 时求圆的半径
第(1)小题要适当启发:由等边三角形ABC入手,得出∠AOB=∠BOC=∠COA=120°, 从而得出 ∠BOD=∠COD=60°。
例3:⑴如图,顺次连结⊙O的两条直径AC和BD的端点,所得的四边形是什么特殊四边形?
⑵如果要把直径为30cm的圆柱形原木锯成一根横截面为正方形的木材,并使截面尽可能地大,应怎样锯?最大横截面面积是多少?
如果这根原木长15m,问锯出地木材地体积为多少立方米(树皮等损耗略去不计)?
分析:教学中应抓好以下几个环节(1)怎样才能使截面尽可能大 应当使截面的各个顶点在圆上,这里用的是合情推理.(2)怎样能使截面成为一个内接于圆0的正方形 引导学生回顾第一问的解答,并问在什么条件矩形就成为正方形.
3. 巩固新知:
P73课内练习1,2
四.小结: 通过这节课的学习,你学到了什么知识?
1.圆的性质在同圆或等圆中,如果两个圆心角、两条弧、两条弦、两个弦心距中有一组量相等,那么它们所对应的其余的各组量都相等。
2.运用关于圆心角,弧,弦,弦心距之间相互关系的定理解决简单的几何问题
五.布置作业:见作业本和课课通3.3-2
第9周第3课时上课时间10月25日(星期三)本学期累计教案36个
课题:讲解作业本的错题和校对“课课通”部分题目
第9周第4课时上课时间10月26日(星期四)本学期累计教案37个
课题:3.4圆周角(1)
教学目标:1、理解圆周叫得概念
2、经历探索圆周角定理的过程
3、掌握圆周角定理和它的推论
4、会运用圆周角定理及其推论解决简单的几何问题
教学重点:圆周角定理
教学难点:圆周角定理的证明要分三种情况讨论,有一定难度。
教学设计:
1、 类比联想,引入新课
1、如图,已知∠AOB=80°,
求弧AB的度数;
②延长AO交⊙O于点C,连结CB,求∠ACB的度数。
2、提问:∠ACB是圆心角吗?(不是)
教师指出:我们把这样的角叫做圆周角,你能模仿圆心角的定义给出圆周角的定义吗?
板书:圆周角的定义:顶点在圆上,两边和圆相交的角叫做圆周角,
练习:(1)练习:判别下列各图形中的角是不是圆周角,并说明理由。
(2)、找出图中所有的圆周角
二、探索圆周角和圆心角的关系
我们学习了与圆有关的两种典型的角 –圆心角和圆周角,在同圆中同弧所对的圆周角和圆心角有什么关系呢?
问题1:请同学们任意画一个圆,并选中一段弧,画出这条弧所对的圆心角和圆周角。
问题2、同弧所对的圆心角和圆周角各有几个? (圆心角一个,圆周角无数个)
问题3、请你猜测同弧所对的圆周角和圆心角大小由什么关系?(∠BAC=∠BOC)
问题4、你能证明你的结论?
学生讨论并寻求证明思路,有困难时老师可以适当点拨。
分三类情况讨论、证明;
第一种情况:圆心在∠BAC的一边上:
∵OA=OC
∴∠BAC=∠C
∵∠BOC是△AOC的外角
∴∠BOC=∠C+∠BAC=2∠BAC
∴∠BAC=∠BOC
第二种情况:当圆心O在∠BAC的外部时
连结A0 并延长,交交⊙O于点D,利用(1)的结果,有∠BAD=∠BOD,
∠DAC=∠DOC,
∴∠BAD+∠DAC=(∠BOD+∠DOC)
即∠BAC=∠BOC
第三种情况:当圆心O在在∠BAC的内部时
连结A0 并延长,交交⊙O于点D,利用(1)的结果,有∠BAD=∠BOD,
∠DAC=∠DOC,
∴∠DAC-∠DAB= (∠DOC-∠DOB)
即∠BAC= ∠BOC
完成证明过程后,把命题改为定理 即
圆周角定理:同弧所对的圆周角等于圆心角的一半。
由于圆心角的度数等于它所对的弧的度数,因此:
(板书)推论1:圆周角的度数等于它所对的弧的度数的一半
通过定理得证明,要使学生明白,要不要分不同情况来证明,主要是看各种情况的证明方法是否相同,相同者不需分,不相同者必须对各种不同情况逐个加以证明,并且做到不重复,不遗漏。
3、 巩固应用
(一)1、已知一条弧所对的圆周角等于50°,则这条弧所对的圆心角为 度,这条弧的度数为 度。
2、已知一条弧的度数为40°,则这条弧所对的圆心角为 度,所对的圆周角为 度。
3、一条弧所对的圆心角的度数为96°,则这条弧的度数为 度,这条弧所对的圆周角
为 度。
小结:圆心角、圆周角、弧的度数关系
4、一条特殊的弧---半圆,它所对的圆周角等于 度。
5、如果一条弧所对的圆周角的度数为90°,那么这条弧所对的圆心角为 度。
由4、5两题得出:
推论2 半圆(直径)所对的圆周角是直角 90°的圆周角所对的弦是直径。
6、如图,已知∠AOB=100°,则∠ACB的度数为 度。
7、一条弦把圆周分成1:2两部分,则弦所对的圆周角的度数为 。(分两种情况)
(二)简单应用
例1:如图;四边形ABCD的四个顶点在⊙O上。
求证;∠B+∠D = 180°
分析:∠B和∠D所对的弧分别是什么? 这两条弧有什么关系?
学生探索 然后交流表达,教师板书示范。
练习:已知:OA、OB、OC都是⊙O的半径,∠AOB=2∠BOC
求证:∠ACB= 2 ∠BAC
证明:
四、课堂总结:这节课我们都学了哪些内容?
五、作业:
1、作业本
2、只给你一把三角尺,你能找出一个圆的圆心吗
(本教案是2006年10月26日在本校九年6班上的公开课教案)
第9周第5课时上课时间10月27日(星期五)本学期累计教案38个
课题:3.4圆周角(2)
教学目标:
1. 经历探索圆周角定理的另一个推论的过程.
2. 掌握圆周角定理的推论“在同圆或等圆中,同弧或等弧所对的圆周角相等,相等的圆周角所对的弧也相等”
3. 会运用上述圆周角定理的推论解决简单几何问题.
教学重点:圆周角定理的推论”在同圆或等圆中,同弧或等弧所对的圆周角相等,相等的圆周角所对的弧也相等”
教学难点:例3涉及圆内角与圆外角与圆周角的关系,思路较难形成,表述也有一定的困难
例4的辅助线的添法.
教学过程:
一、旧知回放:
1、圆周角定义: 顶点在圆上,并且两边都和圆相交的角叫圆周角.
特征:① 角的顶点在圆上.
② 角的两边都与圆相交.
2、圆心角与所对的弧的关系
3、圆周角与所对的弧的关系
4、同弧所对的圆心角与圆周角的关系
圆周角定理: 一条弧所对的圆周角等于它所对的圆心角的一半.
二. 课前测验
1.100 的弧所对的圆心角等于_______,所对的圆周角等于_______。
2、一弦分圆周角成两部分,其中一部分是另一部分的4倍,则这弦所对的圆周角度数为________________。
3、如图,在⊙O中,∠BAC=32 ,则∠BOC=________。
4、如图,⊙O中,∠ACB = 130 ,则∠AOB=______。
5、下列命题中是真命题的是( )
(A)顶点在圆周上的角叫做圆周角。
(B)60 的圆周角所对的弧的度数是30
(C)一弧所对的圆周角等于它所对的圆心角。
(D)120 的弧所对的圆周角是60
三, 问题讨论
如图1,在⊙O中,∠B,∠D,∠E的大小有什么关系 为什么
圆周角定理的推论1:同圆或等圆中,同弧或等弧所对的圆周角相等;
同圆或等圆中,相等的圆周角所对的弧也相等。
四.例题教学:
例2: 已知:如图,在△ABC中,AB=AC,
以AB为直径的圆交BC于D,交AC于E,
求证:⌒ ⌒
BD=DE
证明:连结AD.
∵AB是圆的直径,点D在圆上,
∴∠ADB=90°
∴AD⊥BC,
∵AB=AC,
∴AD平分顶角∠BAC,即∠BAD=∠CAD,
⌒ ⌒
∴BD=DE(同圆或等圆中,相等的圆周角所对弧相等)。
练习:如图,P是△ABC的外接圆上的一点∠APC=∠CPB=60°。
求证:△ABC是等边三角形
例3: 船在航行过程中,船长常常通过测定角度来确定是否会遇到暗礁。如图A,B表示灯塔,暗礁分布在经过A,B两点的一个圆形区域内,C表示一个危险临界点,∠ACB就是“危险角”,当船与两个灯塔的夹角大于“危险角”时,就有可能触礁。
问题:弓形所含的圆周角∠C=50°,问船在航行时怎样才能保证不进入暗礁区
(1)当船与两个灯塔的夹角∠α大于“危险角”时,船位于哪个区域?为什么?
(2)当船与两个灯塔的夹角∠α小于“危险角”时,船位于哪个区域?为什么?
五:练一练:
1.说出命题’圆的两条平行弦所夹的弧相等”的逆命题.原命题和逆命题都是真命题吗 请说明理由.
2.已知:四边形ABCD内接于圆,BD平分∠ABC,且AB∥CD.求证:AB=CD
六.想一想: 如图:AB是⊙O的直径,弦CD⊥AB于点E,G是⌒上任意一点,延长AG,与DC的延长线相交于点F,连接AD,GD,CG,找出图中所有
和∠ADC相等的角,并说明理由.
拓展练习:
1、已知BC为半圆O的直径,AB=AF,AC交BF于点M,过A点作AD⊥BC于D,交BF于E,则AE与BE的大小有什么关系?为什么?
七:小结: 1、本节课我们学习了哪些知识?
2、圆周角定理及其推论的用途你都知道了吗?
第10周第1课时上课时间10月30日(星期一)本学期累计教39个
课题:3.3圆心角和3.4圆周角练习课
一、填空题:
1.如图1,等边三角形ABC的三个顶点都在⊙O上,D是上任一点(不与A、C重合),则∠ADC的度数是________.毛
(1) (2) (3)
2.如图2,四边形ABCD的四个顶点都在⊙O上,且AD∥BC,对角线AC与BC相交于点E,那么图中有_________对相等的角。
3.已知,如图3,∠BAC的对角∠BAD=100°,则∠BOC=_______度.
4.如图4,A、B、C为⊙O上三点,若∠OAB=46°,则∠ACB=_______度.
(4) (5) (6)
5.如图5,AB是⊙O的直径, ,∠A=25°,则∠BOD的度数为________.
6.如图6,AB是半圆O的直径,AC=AD,OC=2,∠CAB= 30 °, 则点O 到CD 的距离OE=______.
二、选择题:
7.如图7,已知圆心角∠BOC=100°,则圆周角∠BAC的度数是( )
A.50° B.100° C.130° D.200°
(7) (8) (9) (10)
8.如图8,A、B、C、D四个点在同一个圆上,四边形ABCD 的对角线把四个内角分成的八个角中,相等的角有( )
A.2对 B.3对 C.4对 D.5对
9.如图9,D是的中点,则图中与∠ABD相等的角的个数是( )
A.4个 B.3个 C.2个 D.1个
10.如图10,∠AOB=100°,则∠A+∠B等于( )
A.100° B.80° C.50° D.40°
11.在半径为R的圆中有一条长度为R的弦,则该弦所对的圆周角的度数是( )
A.30° B.30°或150° C.60° D.60°或120°
12.如图,A、B、C三点都在⊙O上,点D是AB延长线上一点,∠AOC=140°, ∠CBD 的度数是( )
A.40° B.50° C.70° D.110°
三、解答题:
13.如图,⊙O的直径AB=8cm,∠CBD=30°,求弦DC的长.
14.如图,A、B、C、D四点都在⊙O上,AD是⊙O的直径,且AD=6cm,若∠ABC= ∠CAD,求弦AC的长.
15.如图,在⊙O中,AB是直径,CD是弦,AB⊥CD.
(1)P是上一点(不与C、D重合),试判断∠CPD与∠COB的大小关系, 并说明理由.
(2)点P′在劣弧CD上(不与C、D重合时),∠CP′D与∠COB有什么数量关系 请证明你的结论.
16.在足球比赛场上,甲、乙两名队员互相配合向对方球门MN进攻.当甲带球部到A点时,乙随后冲到B点,如图所示,此时甲是自己直接射门好,还是迅速将球回传给乙,让乙射门好呢 为什么 (不考虑其他因素)
17.钳工车间用圆钢做方形螺母,现要做边长为a的方形螺母, 问下料时至少要用直径多大的圆钢
答案:
1.120° 2.3 1 3.160° 4.44° 5.50° 6. 7.A 8.C 9.B 10.C 11.B 12.C
13.连接OC、OD,则OC=OD=4cm,∠COD=60°,故△COD是等边三角形,从而CD= 4cm.
14.连接DC,则∠ADC=∠ABC=∠CAD,故AC=CD.
∵AD是直径,∴∠ACD=90°, ∴AC2+CD2=AD2,即2AC2=36,AC2=18,AC=3.
15.(1)相等.理由如下:连接OD,∵AB⊥CD,AB是直径,
∴,∴∠COB= ∠DOB.
∵∠COD=2∠P,∴∠COB=∠P,即∠COB=∠CPD.
(2)∠CP′D+∠COB=180°.
理由如下:连接P′P,
则∠P′CD=∠P′PD,∠P′PC=∠P′DC.
∴∠P′CD+∠P′DC=∠P′PD+∠P′PC=∠CPD.
∴∠CP′D=180°-(∠P′CD+∠P′DC)=180°-∠CPD=180°-∠COB,
从而∠CP′D+∠COB=180°.
16.迅速回传乙,让乙射门较好,在不考虑其他因素的情况下, 如果两个点到球门的距离相差不大,要确定较好的射门位置,关键看这两个点各自对球门MN的张角的大小,当张角越大时,射中的机会就越大,如图所示,则∠A∠A, 从而B处对MN的张角较大,在B处射门射中的机会大些.
17.a.毛
第10周第2课时上课时间10月31日(星期二)本学期累计教40个
课题:3.5弧长及扇形的面积(1)
教学目标:1、 经历探索弧长计算公式的过程
2、掌握弧长计算公式,并会应用公式解决问题。
教学重点:圆的弧长计算公式
教学难点:例1图形较为复杂,牵涉的知识点较多,并需添加辅助线,思路不易形成。
教学设计:
一、复习(圆周长)
已知⊙O半径为R,⊙O的周长C是多少?C=2πR
这里π=3.14159…,这个无限不循环的小数叫做圆周率.
由于生产、生活实际中常遇到有关弧的长度计算,那么怎样求一段弧的长度呢?
提出新问题:已知⊙O半径为R,求n°圆心角所对弧长.
二、探究新问题、归纳结论
教师组织学生探讨(因为问题并不难,学生完全可以自己研究得到公式).
研究步骤:
(1)圆周长C=2πR;
(2)1°圆心角所对弧长= ;
(3)n°圆心角所对的弧长是1°圆心角所对的弧长的n倍;
(4)n°圆心角所对弧长= .
归纳结论:若设⊙O半径为R, n°圆心角所对弧长l,则
(弧长公式)
(三)理解公式、区分概念
教师引导学生理解:
(1)在应用弧长公式 进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;
(2)公式可以理解记忆(即按照上面推导过程记忆);
(3)区分弧、弧的度数、弧长三概念.度数相等的弧,弧长不一定相等,弧长相等的弧也不一定是等孤,而只有在同圆或等圆中,才可能是等弧.
(四)初步应用
例1、填空:
(1)半径为3cm,120°的圆心角所对的弧长是_______cm;
(2)已知圆心角为150°,所对的弧长为20π,则圆的半径为_______;
(3)已知半径为3,则弧长为π的弧所对的圆心角为_______.
例2、例1 一段圆弧的公路弯道,圆弧的半径是2km,一辆汽车以每小时60km的速度通过弯道,需20秒.求弯道所对的圆心角的度数。(精确到0.1度)
分析:(1)对照弧长公式,那些量是直接已知的,哪个量是要求的?
(2)要求弯道所对圆心角的度数,应先求出什么?
解(略)
例3、 如图,BM是⊙O的直径,四边形ABMN是矩形,D是⊙O上的点,DC⊥AN,与AN交于点C,已知AC=15,⊙O的半径为R=30,求的长。
分析:(1)要求的长,关键是求出所对的圆心角∠BOD的大小。
(2)如何求∠BOD的大小呢?
(3)利用已知条件并通过添加辅助线,构造出△DOB来帮助解决。
课堂练习:作业题第4题
五、总结
知识:圆周长、弧长公式;圆周率概念;
能力:探究问题的方法和能力,弧长公式的记忆方法;初步应用弧长公式解决问题.
六、作业 作业本
第10周第3课时上课时间11月1日(星期三)本学期累计教41个
课题:3.5弧长及扇形的面积(2)
教学目标:1、经历探索扇形面积计算公式的过程;
2、掌握扇形面积的计算公式,并会应用公式解决问题。
教学重点:扇形面积的计算公式。
教学难点:例4涉及弓形面积的计算和流量与流速关系等实际背景,较为复杂。
教学设计:
一、复习圆面积
已知⊙O半径为R,⊙O的面积S是多少?(S=πR2)
我们在求面积时往往只需要求出圆的一部分面积,如图中阴影图形的面积.为了更好研究这样的图形引出一个概念.
扇形:一条弧和经过这条弧的端点的两条半径所组成的图形叫做扇形.
提出新问题:已知⊙O半径为R,求圆心角n°的扇形的面积.
二、探究问题、归纳结论
1、探究问题
教师组织学生对比研究:
(1)圆面积S=πR2;
(2)圆心角为1°的扇形的面积= ;
(3)圆心角为n°的扇形的面积是圆心角为1°的扇形的面积n倍;
(4)圆心角为n°的扇形的面积= .
2、归纳结论:若设⊙O半径为R,圆心角为n°的扇形的面积S扇形,则
S扇形= (扇形面积公式)
(三)理解公式
教师引导学生理解:
(1)在应用扇形的面积公式S扇形= 进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;
(2)公式可以理解记忆(即按照上面推导过程记忆);
提出问题:扇形的面积公式与弧长公式有联系吗?(教师组织学生探讨)
S扇形= lR
想一想:这个公式与什么公式类似?(教师引导学生进行,或小组协作研究)
与三角形的面积公式类似,只要把扇形看成一个曲边三角形,把弧长l看作底,R看作高就行了.这样对比,帮助学生记忆公式.实际上,把扇形的弧分得越来越小,作经过各分点的半径,并顺次连结各分点,得到越来越多的小三角形,那么扇形的面积就是这些小三角形面积和的极限.要让学生在理解的基础上记住公式.
(四)应用
(一)练习:1、已知扇形的圆心角为120°,半径为2,则这个扇形的面积S扇=____.
2、已知扇形面积为 ,圆心角为120°,则这个扇形的半径R=____.
3、已知半径为2的扇形,面积为 ,则它的圆心角的度数=____.
4、已知半径为2cm的扇形,其弧长为 ,则这个扇形的面积,S扇=____.
5、已知半径为2的扇形,面积为 ,则这个扇形的弧长=____.
小结:由上面练习题可知:在弧长、圆心角、半径、扇形面积四个量中只要知道其中的两个量就可以求出另外的两个量,但必须要知道圆的半径。
(二)例题
例3、如图,有一把折扇和一把团扇。已知折扇的骨柄与团扇的直径一样长,折扇扇面的宽度是骨柄长的一半,折扇张开的角度为120 °,问哪一把扇子扇面的面积大?
分析:折扇扇面的面积没有直接的公式可用,应该咋办?(转化为两个扇形的面积之差来计算。
例4、我国著名的引水工程的主干线输水管的直径为2.5m,设计流量为12.73m3 /s.如果水管截面中水面面积如图所示,其中∠AOB=45°,那么水的流速因达到多少m/s.
分析:(1)水的流速与水的流量、截面中水面的面积有什么关系?
(2) 截面中水面的面积即圆的面积与空隙部分弓形面积之差。
(3)弓形面积为扇形AOB与三角形AOB的差。
(三)课堂练习:课本第86页第4题.
五、总结
1、知识:扇形及扇形面积公式S扇形= ,S扇形= lR.
2、方法能力:迁移能力,对比方法;计算能力的培养.
六、作业 见作业本
第10周第4课时上课时间11月2日(星期四)本学期累计教案42个
课题:3.6圆锥的侧面积和全面积
教学目标:1、经历圆锥的侧面积计算公式的探索过程;
2、掌握圆锥的侧面积计算公式,会利用公式进行计算,并会解决实际问题;
3、让学生观察将圆锥的曲面展开在一个平面上的图形。回顾圆锥及其侧面积展开图之间的关系。
教学重点:圆锥侧面积的计算及计算公式
教学难点:圆锥侧面积计算公式的推导过程需要较强的空间想象能力。
教学设计:
[幻灯展示生活中常遇的圆锥形物体,如:铅锤、粮堆、烟囱帽]
前面屏幕上展示的物体都是什么几何体?
在小学我们已学过圆锥,哪位同学能说出圆锥有哪些特征?
答:圆锥是由一个底面和一个侧面围成的,圆锥的底面是一个圆,侧面是一个曲面,从圆锥的顶点到底面圆的距离是圆锥的高。
[教师边演示模型,边启发提问]:
1. 给一圆锥,如何找到它的母线?圆锥的母线应具有什么性质?
2. 现在我把这圆锥的侧面沿它的一条母线剪开,展在一个平面上,
这个展开图是什么图形?
3.圆锥展示图——扇形的弧长l等于圆锥底面圆的什么?
4.扇形的半径其实是圆锥的什么线段?
[扇形的弧长是底面圆的周长,即 ,扇形的半径。就是圆锥的母线]
由于 ,圆锥半径已知则展开图扇形的弧长已知,圆锥母线已知则展开图
扇形的半径已知,因此展开图扇形的面积可求,而这个扇形的面积实质就是圆锥的侧面积,因此圆锥的侧面积也就可求.当然展开图扇形的圆心角也可求.
例1: 圆锥形的烟囱帽的底面直径是80cm,母线长50cm,
计算烟囱帽侧面积.(取3.14,结果保留2个有效数字)
分析:此题直接根据公式,注意最后的答案要根据预定的精确度,用科学记数法写成含两个有效数字的表示形式)
练习:
1.如果圆锥底面半径为4cm,它的侧面积为 ,那么圆锥的母线长为_________.
2.圆锥的底面半径为2 cm,高为cm,则这个圆锥表面积_____________
3一个扇形,半径为30cm,圆心角为120度,用它做成一个圆锥的侧面,那么这个
圆锥的底面半径为_________________
4.圆锥的侧面积是底面积的2倍,这个圆锥的侧面展开图扇形的圆心角是__________
例2、已知一个圆锥的轴截面△ABC是等边三角形,它的表面积为75cm2,求这个圆锥的底面半径和母线的长。
分析:求有关底面半径、母线长、高往往要在直角三角形中
利用勾股定理求得,但此题中只知道表面积所以考虑用方程的思想。
练习:课本作业题的1、2、3
小结:请同学们回顾一下,本堂课我们学了些什么知识?
作业:见作业本
第10周第5课时上课时间11月3日(星期五)本学期累计教案43个
课题:“3.5弧长及扇形的面积、3.6 圆锥的侧面积和全面积”练习
(见实验检测八)
第11周第1课时上课时间11月6日(星期一)本学期累计教案44个
课题:第三章圆的基本性质 复习之一
教学目标:1、通过复习使学生系统掌握本章内容;
2、灵活应用圆的基本性质进行证明和计算。
教学重点和难点:灵活运用垂径定理和逆定理进行证明和计算。
教学设计:
一、知识要点:用填空形式进行(课前发给学生)
1、圆的确定:(1)圆心和半径;(2) 的三点确定一个圆。
2、 点与圆的三种位置关系:
若在平面内的一点P到半径为R的圆心O的距离为d,,则点P 在圆外 ;则点P 在圆上 ;则点P 在圆内 。
3、圆是轴对称图形,它的对称轴是 ,有 条。
4、圆是中心对称图形,对称中心是 ,圆具有绕其圆心旋转的 性。
5、垂径定理:垂直于弦的直径 这条弦, 弦所对的两条弧。
逆定理:平分弦(不是弦)的直径 ;平分弦所对的弧的直径 。
6、圆心角、弧、弦、弦心距之间的关系:在同圆或等圆中,如果 、
、 、 中有一组量相等,那么它们所对应的其余各组量都相等。
二、典型例题解析
例1、(1)下列命题中正确的是( )
A、 圆周角等于圆心角的一半; B、相等的圆周角所对的弧相等;
C、等弧所对的圆周角相等; D、任意三点可以确定一个圆。
(2)⊙O的半径为10 cm ,弦AB∥CD,阿布=12cm ,CD =16cm,则AB和CD的距离为( )
A、2cm B、14cm C、2cm或14cm D、10cm 或20cm
(3)如图,⊙O的直径为10,弦AB=8,P是弦AB上的一个动点,那么OP的长的取值范围是 。
(4)如果AB为⊙O的直径,弦CD⊥AB,垂足为E,那么下面结论中错误的是( )
A、CE=DE B、 C、∠BAC=∠BAD D、AC>AD
例2、
A
B
C
D
O
E
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
A
B
C
D
O
E
⌒
⌒
⌒
⌒
⌒
⌒
⌒
O
A
B
C
⌒
⌒
B
C
O
∠AOB=∠COD
AB=CD
OE=OF
AB=CD
⌒
⌒
O
C
B
A
A
C
O
A
A
B
C
D
A
B
D
G
F
C
E
O
课题:3.1圆 (1)
教学目标:
1、经历形成圆的概念的过程,经历探索点与圆的位置关系得过程。
2、理解圆的概念,了解点与圆的位置关系;
3、会在简单条件下判断点与圆的位置关系。
教学重点:圆、弦和弧的概念,弧的表示法和点与圆的位置关系。
教学难点:点与圆的位置关系
教学过程:
一、创设情景,引入新课
1、在小学我们已经学过一些圆的知识,并且知道圆不仅在几何中占有极其重要的地位,而且在日常生活和生产实践中有着广泛的应用,你能举例说明我们周围那些物体是圆形的吗?
在学生回答的基础上,教师总结:实际生活中圆形物体的例子很多(出示一些投影图象)
2、提问:人们为什么把车轮做成圆形的?
在学生回答的基础上,教师指出:这是因为圆具有一些特殊的性质,在这一章里我们将系统研究:什么是圆?圆有哪些性质?
二、描述圆的发生过程,给出圆的定义和有关概念
1、如何用圆规画出一个圆?
2、要在操场上画一个半径为5米的大圆,如何画呢?
3、从实践中给出圆的定义
在同一平面内线段OP绕它的一个端点O旋转一周,另一个端点P所经过的封闭曲线叫做圆,定点O叫做圆心,定长 OP叫做半径。
以点0为圆心的圆记作⊙O,读作“圆O”
(利用几何画板动态演示)
4、圆的有关概念
1)连结圆上任意两点的线段叫做弦,如图BC.经过圆心的弦是直径,
图中的AB。直径等于半径的2倍.
(2)圆上任意两点间的部分叫做圆弧,简称弧.弧用符号“⌒”表示.
小于半圆的弧叫做劣弧,如图中以B、C为端点的劣弧记做“⌒BC”;
大于半圆的弧叫做优弧,优弧要用三个字母表示,如图中的.
(3)半径相等的两个圆能够完全重合,我们把半径相等的两个圆叫做
等圆.例如,图中的⊙O1和⊙O2是等圆.
圆心相同,半径不相等的圆叫做同心圆。(学生画同心圆)
5、完成课本第58页的做一做
三、点和圆的位置关系
同学们看过奥运会的射击比赛吗?射击的靶子是由许多圆组成的,射击的成绩是由击中靶子不同位置所决定的;右图是一位运动员射击10发子弹在靶上留下的痕迹。你知道这个运动员的成绩吗?请同学们算一算。(击中最里面的圆的成绩为10环,依次为9、8、…、1环)
这一现象体现了平面上的点与圆的位置关系,如何判断点与圆的位置关系呢?我们知道圆上的所有点到圆心的距离都等于半径,若点在圆上,那么这个点到圆心的距离等于半径,若点在圆外,那么这个点到圆心的距离大于半径,若点在圆内,那么这个点到圆心的距离小于半径。
如图,设⊙O的半径为r,A点在圆内,B点在圆上,C点在圆外,那
OA<r, OB=r, OC>r.反过来也成立,即
若点A在⊙O内
若点A在⊙O上
若点A在⊙O外
思考与练习
(1)课内练习第2题
(2)例题:例1 如图所示,在A地正北80m的B处有一幢民房,正西100m的C处有一变电设施,在BC的中点D处是一古建筑。因施工需要,必须在A处进行一次爆破。为使民房、变电设施、古建筑都不遭到破坏,问爆破影响面的半径应控制在什么范围内?
(3)如图,在A岛附近,半径约250km的范围内是一暗礁区,往北300km有一灯塔B,往西400km有一灯塔C。现有一渔船沿CB航行,问渔船会进入暗礁区吗?(课本第60页第6题)
四、课堂小结:
这节课学习了那些内容?
1、圆的定义和有关概念
2、点和圆的位置关系
五、作业
见作业本
第8周第2课时上课时间10月17日(星期二)本学期累计教案29个
课题:3.1圆(2)
教学目标:
知识目标:
1、通过问题的解决过程,使学生明确三角形的外接圆、三角形的外心、圆的内接三角形的概念,理解“不在同一直线上的三点确定一个圆”。
2、使学生能熟练掌握应用尺规“过不在同一直线上三点作圆”的方法。
3、向学生渗透转化、分类讨论等数学思想方法,为今后继续进一步学习数学打下基础。
能力目标:
1、通过学生自己动手作图,在动手参与的过程中探索、发现科学知识,进一步提高学生动手做的积极性。
2、提高学生应用数学知识解决生活中实际问题的能力。
情感目标:
1、增强学生的数学应用意识,提高学生学习数学的兴趣和积极性。
2、培养学生树立良好的创新意识、养成永无止境的科学探索精神。
教学重点:过不在一直线上的三点作圆的方法
教学难点:如何确定圆的思维过程
教学过程:
一:创设情境、提出问题
投影片出示问题:(破镜重圆)
现有一块打碎的圆形玻璃镜子残片,想重新去玻璃店配一块同样大小的圆形玻璃镜子,请问怎样去配制呢?
思考:如何解决这一实际问题?下面我们共同探寻解决这一问题的办法
二、实践活动,探究新知
探究①:过一个已知点A能否作圆?如果能,可以作几个? (让学生动手去完成)
学生讨论并发现:过点A所作圆的圆心在哪儿(圆心不定)?半径多大(半径不定)?可以作几个这样的圆(无数个)?
探究②:过已知两点A、B能否作圆?如果能,可以作几个? 圆心在哪里?(学生动手去完成)
学生继续讨论并发现:它们的圆心到A、B两点的距离怎样?能用式子表示吗(OA=OB) 圆心在哪里(在直线AB的垂直平分线上)?过点A、B两点的圆有几个(无数个)?
探究③:过同一平面内三个点A、B、C是否可以作圆?的情况会怎样呢
分两种情况研究:
(一)求作一个圆,使它经过不在一直线上三点A、B、C,
已知:不在一直线上三点A、B、C,求作一个圆,使它同时经过点A、B、C。(学生口述作法,教师示范作图过程)
学生讨论并发现:这样一共可作几个圆(一个)?圆心在哪里(线段AB、AC、BC的垂直平分线的交点)?到A、B、C三点的距离怎样?(OA=OB=OC)
(二)过在一直线上的三点A、B、C可以作几个圆?(不能作出)
发现结论:由上可知,过一点可作无数个圆,过已知两点可以作无数个圆,过不在同一直线上的三点可以作一个圆,并且只能作一个圆。
定理:过不在同一直线上的三点确定一个圆
强调:(1)“不在同一直线上”这个条件不可忽略,只有当三个点不在同一直线上才能确定一个圆。
(2)“确定”一词理解为“有且只有”
由上可知,经过三角形的三个顶点可以做一个圆。
因此三角形的三个顶点确定一个圆,这个圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,它是三角形三条边的垂直平分线的交点,这个三角形叫做圆的内接三角形。
(1)“接“是说明三角形的顶点和圆的关系,即圆经过三角形的各顶点;
(2)而“内“、”外“是相对的概念,以一个图形为准明说明另一个图形在它的里面或外面,如”三角形的外接圆“是以三角形为准,说明圆在三角形的外面。
如图:⊙O称为△ABC的外接圆,△ABC称为⊙O的内接三角形,O为三角形ABC的外心。
三、应用新知
1、解决引例的问题(让学生口述解决的办法)
①在残片上任取三点A、B、C,连结AB、AC
②分别作AB、AC的垂直平分线,并交于一点O,O为圆心。
③连结OA,以OA为半径画圆即可。
2、精心的判一判
(1)过两点可以作无数个圆。( )
(2)经过三点一定可以做一个圆。( )
(3)顶点都在圆上的三角形叫做圆的外接三角形。( )
(4)任意一个三角形一定有一个外接圆,并且只有一个外接圆。( )
(5)任意一个圆一定有一个内接三角形,并且只有一个内接三角形。( )
(6)三角形的外心就是这个三角形两边垂直平分线的交点。( )
(7)三角形的外心到三边的距离相等。( )
3、仔细的填一填:
如图:⊙O是△ABC的 ______ 圆,△ABC是⊙O的 ________ 三角形,O是△ABC的 ______ 心,它是 __________ 线的交点,到三角形 __________ 距离相等。
4、认真做一做:作出下列三角形的外接圆,并比较这三个三角形的外心的位置,你得到什么结论?
发现:
(1)锐角三角形的外心在三角形的内部;
(2)钝角三角形的外心在三角形的外部;
(3)直角三角形的外心在斜边的中点处。
四、深化与延伸
1、如图,已知在Rt△ABC中,∠C=90°,AC=5cm,BC=12cm,则△ABC的面积为 。
2、如图,在等腰三角形ABC中,AB=AC=13cm,BC=10cm,则△ABC的外接圆的半径为 。
五、课堂小结
通过这节课你学到哪些知识?还有哪些困惑?
六、作业:
1、作业本
2、动手做一做
(1) 怎样找出一个圆形纸片的圆心?(请你想出尽可能多的方法)
(2)过四个点能否作一个圆
第8周第3课时上课时间10月18日(星期三)本学期累计教案30个
课题:3.2圆的轴对称性(1)
教学目标
1.使学生理解圆的轴对称性.
2.掌握垂径定理.
3.学会运用垂径定理解决有关弦、弧、弦心距以及半径之间的证明和计算问题.
教学重点
垂径定理是圆的轴对称性的重要体现,是今后解决有关计算、证明和作图问题的重要依据,它有着广泛的应用,因此,本节课的教学重点是:垂径定理及其应用.
教学难点
垂径定理的推导利用了圆的轴对称性,它是一种运动变换,这种证明方法学生不常用到,与严格的逻辑推理比较,在证明的表述上学生会发生困难,因此垂径定理的推导是本节课的难点.
教学关键
理解圆的轴对称性.
教学环节的设计
这节课我通过七个环节来完成本节课的教学目标,它们是:
复习提问,创设情境;引入新课,揭示课题;讲解新课,探求新知;应用新知,体验成功;
目标训练,及时反馈;总结回顾,反思内化;布置作业,巩固新知.
一、复习提问,创设情境
1.教师演示:将一等腰三角形沿着底边上的高对折,启发学生共同回忆等腰三角形是轴对称图形,同时复习轴对称图形的概念;
2.提出问题:如果以这个等腰三角形的顶点为圆心,腰长为半径作圆,得到的圆是否是轴对称图形呢?(教师用教具演示,学生自己操作)
二、引入新课,揭示课题
1.在第一个环节的基础上,引导学生归纳得出结论:
圆是轴对称图形,每一条直径所在的直线都是对称轴.
强调:
(1)对称轴是直线,不能说每一条直径都是它的对称轴;
(2)圆的对称轴有无数条.
判断:任意一条直径都是圆的对称轴( )
设计意图:让学生更好的理解圆的轴对称轴新性,为下一环节探究新知作好准备.
三、讲解新课,探求新知
先按课本进行合作学习
1.任意作一个圆和这个圆的任意一条直径CD;
2.作一条和直径CD的垂线的弦,AB与CD相交于点E.
提出问题:把圆沿着直径CD所在的直线对折,你发现哪些点、线段、圆弧重合?
在学生探索的基础上,得出结论:(先介绍弧相等的概念)
①EA=EB;② AC=BC,AD=BD.
理由如下:∵∠OEA=∠OEB=Rt∠,根据圆的轴轴对称性,可得射线EA与EB重合,
∴点A与点B重合,弧AC和弧BC重合,弧AD和弧BD重合.
∴ EA=EB, AC=BC,AD=BD.
思考:你能利用等腰三角形的性质,说明OA平分CD吗?(课内练习1)
注:老教材这个内容放在圆心角、圆周角之后,垂径定理完全可以不用圆的轴对称性来证,可用等腰三角形的性质来证明,现在只能证前面一个(略).
然后把此结论归纳成命题的形式:
垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧.
垂径定理的几何语言
∵CD为直径,CD⊥AB(OC⊥AB)
∴ EA=EB, AC=BC,AD=BD.
四、应用新知,体验成功
例1 已知AB,如图,用直尺和圆规求作这条弧的中点.(先介绍弧中点概念)
作法:
⒈连结AB.
⒉作AB的垂直平分线 CD, 交弧AB于点E.
点E就是所求弧AB的中点.
变式一: 求弧AB的四等分点.
思路:先将弧AB平分,再用同样方法将弧AE、弧BE平分.
(图略)
有一位同学这样画,错在哪里?
1.作AB的垂直平分线CD
2.作AT、BT的垂直平分线EF、GH(图略)
教师强调:等分弧时一定要作弧所对的弦的垂直平分线.
变式二:你能确定弧AB的圆心吗?
方法:只要在圆弧上任意取三点,得到三条弦,画其中两条弦的垂直平分线,交点即为圆弧的圆心.
例2 一条排水管的截面如图所示.排水管的半径OB=10,水面宽AB=16,求截面圆心O到水面的距离OC .
思路:
先作出圆心O到水面的距离OC,即画 OC⊥AB,∴AC=BC=8,
在Rt△OCB中,
∴圆心O到水面的距离OC为6.
例3 已知:如图,线段AB与⊙O交于C、D两点,且OA=OB .求证:AC=BD .
思路:
作OM⊥AB,垂足为M, ∴CM=DM
∵OA=OB , ∴AM=BM , ∴AC=BD.
概念:圆心到圆的一条弦的距离叫做弦心距.
小结:
1.画弦心距是圆中常见的辅助线;
2.半径(r)、半弦、弦心距(d)组成的直角三角形是研究与圆有关问题的主要思路,它们之间的关系:弦长.
注:弦长、半径、弦心距三个量中已知两个,就可以求出第三个.
五、目标训练,及时反馈
1.已知⊙0的半径为13,一条弦的AB的弦心距为5,则这条弦的弦长等于 .
答案:24
2.如图,AB是⊙0的中直径,CD为弦,CD⊥AB于E,则下列结论中不一定成立的是( )
A.∠COE=∠DOE B.CE=DE C.OE=BE D.BD=BC
答案:C
3.过⊙O内一点M的最长弦长为10cm,最短弦长为8cm,那么OM长为( )
A.3 B.6cm C. cm D.9cm
答案:A
注:圆内过定点M的弦中,最长的弦是过定点M的直径,最短的弦是过定点M与OM垂直的弦,此结论最好让学生记住,课本作业题也有类似的题目.
4.如图,⊙O的直径为10,弦AB长为8,M是弦AB上的动点,则OM的长的取值范围是( )
A.3≤OM≤5 B.4≤OM≤5 C.3
5. 已知⊙O的半径为10,弦AB∥CD,AB=12,CD=16,则AB和CD的距离为 .
答案:2或24
注:要分两种情况讨论:(1)弦AB、CD在圆心O的两侧;(2)弦AB、CD在圆心O的同侧.
6.如图,已知AB、AC为弦,OM⊥AB于点M, ON⊥AC于点N ,BC=4,求MN的长.
思路:由垂径定理可得M、N分别是AB、AC的中点,
所以MN=BC=2.
六、总结回顾,反思内化
师生共同总结:
1.本节课主要内容:(1)圆的轴对称性;(2)垂径定理.
2.垂径定理的应用:(1)作图;(2)计算和证明.
3.解题的主要方法:
(1)画弦心距是圆中常见的辅助线;
(2)半径(r)、半弦、弦心距(d)组成的直角三角形是研究与圆有关问题的主要思路,它们之间的关系:弦长.
七、布置作业, 巩固新知
P75作业题1~6,第7题选做.
第8周第4课时上课时间10月19日(星期四)本学期累计教案31个
课题:3.2圆的轴对称性(2)
教学目标
1.使学生掌握垂径定理及其推论,并会用垂径定理及其推论解决有关证明、计算和作图问题;
2.使学生了解垂径定理及其推论在实际中的应用,培养学生把实际问题转化为数学问题的能力和计算能力,结合应用问题向学生进行爱国主义教育.
教学重点和难点
垂径定理的两个推论是重点;由定理推出推论1是难点.
教学过程设计
一、从学生原有的认知结构提出问题
1.画图叙述垂径定理,并说出定理的题设和结论.(由学生叙述)
2.结合图形7-35,教师引导学生写出垂径定理的下述形式:
题设 结论
线CD平分弦AB
指出:垂径定理是由两个条件推出三个结论,即由①②推出③④⑤.
提问:如果把题设和结论中的5条适当互换,情况又会怎样呢 引出垂径定理推论的课题
. 二、运用逆向思维方法探讨垂径定理的推论
1.引导学生观察图形,选①③为题设,可得:
由于一个圆的任意两条直径总是互相平分的,但是它们不一定是互相垂直的,所以要使上面的题设能够推出上面的结论,还必须加上“弦AB不是直径”这一条件.
这个命题是否为真命题,需要证明,结合图形请同学叙述已知、求证,教师在黑板上写出.
已知:如图7-36,在⊙O中,直径CD与弦AB(不是直径)相交于E,且E是AB的中点.
求证:CD⊥AB,.
分析:要证明CD⊥AB,即证OE⊥AB,而E是AB的中点,即证OE为AB的中垂线.由等腰三角形的性质可证之.利用垂径定理可知AC=BC,AD=BD.
证明:连结OA,OB,则OA=OB,△AOB为等腰三角形.
因为E是AB中点,所以OE⊥AB,即CD⊥AB,
又因为CD是直径,所以
2. 若选①④为题设,可得:
以上命题用投影打出,引导学生自己证出?
3.根据上面具体的分析,在感性认识的基础上,引导学生用文字叙述其中最常用的二个命题,教师板书出垂径定理的推论1.
推论1 (1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;
(2) 平分弦所对的一条弧的直径,垂直平分弦并且平分弦所对的另一条弧.
三、应用举例,变式练习
例1 平分已知.
引导学生画图,写已知、求作.
已知: (图7-38),求作:的中点.
分析:弦的垂直平分线经过圆心,并且平分弦所对的两条弧.因此,连结AB,作弦AB的垂直平分线,它一定平分.
作法:(由学生口述,教师板书,师生共同作图)
练习1 四等分已知.
引导学生在平分的基础上,进一步平分AM和BM,即可四等分AB.
作图后,提问:四等分弦AB是否可四等分,为什么 如图7-39所示.
在学生回答的基础上,强调:这种作法是错误的,虽然在等分时作法是对的,但是在等分和时是错误的,因为AT,BT不是和所对的弦.因此AT,BT的垂直平分线不能平分和,请同学们务必注意.
练习2 按图7-40,填空:在⊙O中
(1)若MN⊥AB,MN为直径;则 , , ;
(2)若AC=BC,MN为直径;AB不是直径,则 , , ;
(3)若MN⊥AB,AC=BC,则 , , ;
(4)若=,MN为直径,则 , , .
此练习的目的是为了帮助学生掌握垂径定理及推论1的条件和结论.
例2 1300多年前,我国隋代建造的赵州石拱桥(图7-41)的桥拱是圆弧形,它的跨度(弧
所对的弦的长)为37.4米,拱高(弧的中点到弧的距离,也叫弓形高)为7.2米,求桥拱的半径.(精确到0.1米)
首先可借此题向学生介绍“赵州桥”,对学生进行爱国主义教育,同
时也可激发学生学习数学的兴趣.
关于赵州桥的说明:
赵州桥又名“安济桥”,位于河北省赵县城南交河上,是我国现存的著名古代大石拱桥、
?隋开皇大业年间(590~608)由李春创建.桥单孔,全长50.82米,桥面宽约10米,跨径约
为37米,弧形平缓,拱圈为28条并列的石条组成,上设四个小拱,既减轻重量,节省材料,
又便于排洪,且增美观?在世界桥梁史上,其设计与工艺之新为石拱桥的卓越典范,跨度之
大在当时亦属首创,反映了我国古代劳动人民的智慧与才能.
分析:(1)首先说明跨度、拱高等概念,然后引导学生设法把实际问题转化为数学问题
,并画出几何图形(图7-42),且一边画图一边解释:桥拱是圆弧形,以O为圆心,R为半径画
出一段圆弧表示桥拱,弦AB表示桥的跨度,即AB=37.4米,的中点C到线段AB的距离为7
.2米.
这样我们就可以根据实际问题,参照上图写出数学问题的已知和求解.
(2)实际问题已转化为数学问题,下面讨论如何解决这个问题.
启发学生观察图形、发现:对于,如果经过圆心O作弦AB的垂线OD,D为垂足,并延长交于点C,那么根据垂径定理可知,OD平分弦,OC平分弧,即C点为AB的中点,CD就是
拱高,这样做出的图形符合题意.
根据勾股定理,在Rt△AOD中就可求出半径R. 解题过程,参考课本. 对于此题,学生往往是过的中点C先作出弓形高CD,即过C作CD⊥AB,垂足为D,如果是这样的话,可引导学生根据垂径定理,首先证明直线CD经过圆心O,仍然可利用勾股定理,求出半径R.
说明:此题的解题思路是,经过圆心作弦的垂线,说明它平分弦且平分弦所对的弧?也
可以经过弧的中点作弦的垂线,说明它平分弦且经过圆心.解决这类问题时,只要抓住弦长
、弦心距、弓形高及半径之间的关系,已知其中的两个量,可以求出其它两个未知量,这种
思考方法今后要经常用到.
例3 已知;如图7-43,⊙O半径为6厘米,弦AB与半径OA的夹角为30°.
求:弦AB的长.
分析:已知圆的半径和半径与弦的夹角.要求弦长,只要利用圆的半径、弦长、圆心到
弦的距离之间的关系即可.过圆心O作AB的垂线段OD,解Rt△AOD,求出AD即可求得AB.
解:作OD⊥AB于D,则AD=DB,
在Rt△AOD中,因为∠DAO=30°
练习3 如图7-44(厘米)
在直径为650毫米的圆柱形油槽内装入一些油后,截面如图所示.若油面宽AB=600毫米,求油的最大深度.
通过此练习题,进一步培养学生把实际问题转化为数学问题的能力.再一次明确弦长a、弦心距d、半径r及弓形高h之间的关系.(图7-45)
四、师生共同小结
问:这节课我们学习了哪些主要内容
在学生回答的基础上,用投影出示垂径定理及其推论的基本图形,如图7-46.
指出:若垂径定理或推论中的某一个成立,则
(1) △CAB,△OAB,△DAB都是等腰三角形,弦AB是它们公共的底边,直径CD是它
们的顶角平分线和底边的垂直平分线.
(2) △ACD和△BCD是全等的直角三角形,直径CD是它们公共的斜边,AE,BE分别是斜边
(2)上的高,AO,BO分别是斜边上的中线?在这两个三角形中可以运用直角三角形的一系列性质.
(3
通过应用题的学习,培养把实际问题抽象成数学问题的意识,从而提高转化能力和计算能力.
六、布置作业:见作业本
第8周第5-6课时上课时间10月20日(星期五)本学期累计教案33个
课题:3.1——3.2 练习课(见实验检测六)
第9周第1课时上课时间10月23日(星期一)本学期累计教案34个
课题:3.3圆心角(1)
教学目标:1、经历探索圆的中心对称性和旋转不变性的过程,
2、理解圆心角的概念,并掌握“在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦相等”的定理(圆心角定理)。
3、体验利用旋转变换来研究圆的性质的思想方法。
教学重点:圆心角定理
教学难点:根据圆的旋转不变性推出圆心角定理,需用到图形的旋转变换。
教学内容设计
(一)圆的对称性和旋转不变性
学生动手画圆,对折、观察得出:圆是轴对称图形和中心对称图形;圆的旋转不变性.
引出圆心角和弦心距的概念:
圆心角定义:顶点在圆心的角叫圆心角.
弦心距定义:从圆心到弦的距离叫做弦心距.
(二)圆心角、弧、弦、弦心距之间的关系
应用电脑动画(实验)观察,在同圆等圆中,圆心角变化时,圆心角所对应的弧、弦、弦心距之间的关系,得出定理的内容.这样既培养学生观察、比较、分析和归纳知识的能力,又可以充分调动学生的学习的积极性.
定理:在同圆等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对弦的弦心距也相等.
(三)应用、巩固和反思 ( http: / / www.teachercn.com / Xxyw / Fs / " \t "_blank )
1、判断题,下列说法正确吗?为什么?
如图,因为∠AOB=∠COD,所以AB= CD, =.
2、例1、用直尺和圆规把⊙O四等分
(可以让学生先尝试自己找出作法,在学生尝试过程中,教师作适当的启发)
提问:如何把圆八等分
(四)深化提高,得出推论
先让学生观察右图,提问:圆周所对的圆心角有多大?(360°)请大家想象一下,当把顶点在圆心的圆周等分成360份后,相应的把整个圆分成多少份?(360份)这时,每一份圆心角即1°的圆心角就对着1°的弧,我们把这一份的弧叫做1°的弧。
提问:n°的圆心角所对的弧是几度?
推论:圆心角的度数等于它所对的弧的度数。
练习:(1)你还有什么方法把圆八等分?
(2)课本第70页课内练习1、2、3
(六)小结:学生自己归纳,老师指导.
知识:①圆的对称性和旋转不变性;②圆心角、弧、弦、弦心距之间关系,它反映出在圆中相等量的灵活转换.
能力和方法:①增加了证明角相等、线段相等以及弧相等的新方法;②实验、观察、发现新问题,探究和解决问题的能力.
(七)作业:
(1)课本第71页作业题 和作业本
(2)圆心角定理是在同圆和等圆这个大前提下,已知圆心角相等,得出其余的三组量相等,请同学们课后思考,在这个大前提下,把圆心角相等与结论中的任何一个交换位置,可以得到新命题,这三个是真命题吗?如何证明?
第9周第2课时上课时间10月24日(星期二)本学期累计教案35个
课题:3.3圆心角(2)
教学目标:
1. 经历探索圆心角定理的逆定理的过程;
2. 掌握”在同圆或等圆中,如果两个圆心角、两条弧、两条弦,两个圆心距中有一对量相等,那么它们所对应的其余各对量都相等”这个圆的性质;
3. 会运用关于圆心角,弧,弦,弦心距之间相互关系的定理解决简单的几何问题..
教学重点与难点:
教学重点: 关于圆心角,弧,弦,弦心距之间相互关系的性质
教学难点:例2(1)题,例3涉及四边形,圆等较多知识点,且思路不易形成,是本节的教学难点
教学过程:
1. 复习旧知,创设情景:
1. 圆具有哪些性质
2. 如图,已知:⊙O上有两点A、B,连结OA、OB,作∠AOB的角平分线交⊙O于点C,连结AC、BC.图中有哪些量是相等的
复习圆心角定理的内容.
3. 请写出圆心角定理的逆命题,并证明它们的正确性.
(1).逆命题 : 在同圆或等圆中,相等的弧所对的圆心角相等,所对的弦相等,所对的弦的弦心距相等。
(2) 逆命题 : 在同圆或等圆中,相等的弦所对的圆心角相等,所对的弧相等,弦的弦心距相等。
(3)逆命题 : 在同圆或等圆中,相等的弦心距对应弦相等,弦所对的圆心角相等,所对的弧相等。
结合图形说出已知和求证并给出简要的证明过程
由此引出新课.
2. 新课讲解
1、运用上面的结论来解决下面的问题:
已知:如图,AB、CD是⊙O的两条弦,OE、OF为AB、CD的弦心距,根据本节定理及推论填空:
(1)如果AB=CD,那么
_____________,________,____________。
(2)如果OE=OF,那么
_____________,________,____________。
(3)如果弧AB=弧CD 那么
______________,__________,____________。
(4)如果∠AOB=∠COD,那么
_________,________,_________。
2、上面的练习说明:
以下的四个量中只要有一个量相等,就可以得到
其余的量相等:
⑴∠AOB=∠COD⑵AB=CD
⑶OE=OF⑷弧AB=弧CD
3、一般地,圆有下面的性质
在同圆或等圆中,如果两个圆心角、两条弧、两条弦、两个弦心距中有一组量相等,那么它们所对应的其余的各组量都相等。
4.例题讲解:
例2:如图,等边三角形ABC内接于⊙O,连结OA,OB,OC.
⑴ ∠AOB 、∠COB、 ∠AOC分别为多少度?
⑵延长AO,分别交BC于点P,弧BC于点D,连结BD,CD.判断三角形OBD是哪一种特殊三角形?
⑶判断四边形BDCO是哪一种特殊四边形,并说明理由。
⑷若⊙O的半径为r,求等边ABC三角形的边长?
⑸若等边三角形ABC的边长r,求⊙O的半径为 多少?
当r = 时求圆的半径
第(1)小题要适当启发:由等边三角形ABC入手,得出∠AOB=∠BOC=∠COA=120°, 从而得出 ∠BOD=∠COD=60°。
例3:⑴如图,顺次连结⊙O的两条直径AC和BD的端点,所得的四边形是什么特殊四边形?
⑵如果要把直径为30cm的圆柱形原木锯成一根横截面为正方形的木材,并使截面尽可能地大,应怎样锯?最大横截面面积是多少?
如果这根原木长15m,问锯出地木材地体积为多少立方米(树皮等损耗略去不计)?
分析:教学中应抓好以下几个环节(1)怎样才能使截面尽可能大 应当使截面的各个顶点在圆上,这里用的是合情推理.(2)怎样能使截面成为一个内接于圆0的正方形 引导学生回顾第一问的解答,并问在什么条件矩形就成为正方形.
3. 巩固新知:
P73课内练习1,2
四.小结: 通过这节课的学习,你学到了什么知识?
1.圆的性质在同圆或等圆中,如果两个圆心角、两条弧、两条弦、两个弦心距中有一组量相等,那么它们所对应的其余的各组量都相等。
2.运用关于圆心角,弧,弦,弦心距之间相互关系的定理解决简单的几何问题
五.布置作业:见作业本和课课通3.3-2
第9周第3课时上课时间10月25日(星期三)本学期累计教案36个
课题:讲解作业本的错题和校对“课课通”部分题目
第9周第4课时上课时间10月26日(星期四)本学期累计教案37个
课题:3.4圆周角(1)
教学目标:1、理解圆周叫得概念
2、经历探索圆周角定理的过程
3、掌握圆周角定理和它的推论
4、会运用圆周角定理及其推论解决简单的几何问题
教学重点:圆周角定理
教学难点:圆周角定理的证明要分三种情况讨论,有一定难度。
教学设计:
1、 类比联想,引入新课
1、如图,已知∠AOB=80°,
求弧AB的度数;
②延长AO交⊙O于点C,连结CB,求∠ACB的度数。
2、提问:∠ACB是圆心角吗?(不是)
教师指出:我们把这样的角叫做圆周角,你能模仿圆心角的定义给出圆周角的定义吗?
板书:圆周角的定义:顶点在圆上,两边和圆相交的角叫做圆周角,
练习:(1)练习:判别下列各图形中的角是不是圆周角,并说明理由。
(2)、找出图中所有的圆周角
二、探索圆周角和圆心角的关系
我们学习了与圆有关的两种典型的角 –圆心角和圆周角,在同圆中同弧所对的圆周角和圆心角有什么关系呢?
问题1:请同学们任意画一个圆,并选中一段弧,画出这条弧所对的圆心角和圆周角。
问题2、同弧所对的圆心角和圆周角各有几个? (圆心角一个,圆周角无数个)
问题3、请你猜测同弧所对的圆周角和圆心角大小由什么关系?(∠BAC=∠BOC)
问题4、你能证明你的结论?
学生讨论并寻求证明思路,有困难时老师可以适当点拨。
分三类情况讨论、证明;
第一种情况:圆心在∠BAC的一边上:
∵OA=OC
∴∠BAC=∠C
∵∠BOC是△AOC的外角
∴∠BOC=∠C+∠BAC=2∠BAC
∴∠BAC=∠BOC
第二种情况:当圆心O在∠BAC的外部时
连结A0 并延长,交交⊙O于点D,利用(1)的结果,有∠BAD=∠BOD,
∠DAC=∠DOC,
∴∠BAD+∠DAC=(∠BOD+∠DOC)
即∠BAC=∠BOC
第三种情况:当圆心O在在∠BAC的内部时
连结A0 并延长,交交⊙O于点D,利用(1)的结果,有∠BAD=∠BOD,
∠DAC=∠DOC,
∴∠DAC-∠DAB= (∠DOC-∠DOB)
即∠BAC= ∠BOC
完成证明过程后,把命题改为定理 即
圆周角定理:同弧所对的圆周角等于圆心角的一半。
由于圆心角的度数等于它所对的弧的度数,因此:
(板书)推论1:圆周角的度数等于它所对的弧的度数的一半
通过定理得证明,要使学生明白,要不要分不同情况来证明,主要是看各种情况的证明方法是否相同,相同者不需分,不相同者必须对各种不同情况逐个加以证明,并且做到不重复,不遗漏。
3、 巩固应用
(一)1、已知一条弧所对的圆周角等于50°,则这条弧所对的圆心角为 度,这条弧的度数为 度。
2、已知一条弧的度数为40°,则这条弧所对的圆心角为 度,所对的圆周角为 度。
3、一条弧所对的圆心角的度数为96°,则这条弧的度数为 度,这条弧所对的圆周角
为 度。
小结:圆心角、圆周角、弧的度数关系
4、一条特殊的弧---半圆,它所对的圆周角等于 度。
5、如果一条弧所对的圆周角的度数为90°,那么这条弧所对的圆心角为 度。
由4、5两题得出:
推论2 半圆(直径)所对的圆周角是直角 90°的圆周角所对的弦是直径。
6、如图,已知∠AOB=100°,则∠ACB的度数为 度。
7、一条弦把圆周分成1:2两部分,则弦所对的圆周角的度数为 。(分两种情况)
(二)简单应用
例1:如图;四边形ABCD的四个顶点在⊙O上。
求证;∠B+∠D = 180°
分析:∠B和∠D所对的弧分别是什么? 这两条弧有什么关系?
学生探索 然后交流表达,教师板书示范。
练习:已知:OA、OB、OC都是⊙O的半径,∠AOB=2∠BOC
求证:∠ACB= 2 ∠BAC
证明:
四、课堂总结:这节课我们都学了哪些内容?
五、作业:
1、作业本
2、只给你一把三角尺,你能找出一个圆的圆心吗
(本教案是2006年10月26日在本校九年6班上的公开课教案)
第9周第5课时上课时间10月27日(星期五)本学期累计教案38个
课题:3.4圆周角(2)
教学目标:
1. 经历探索圆周角定理的另一个推论的过程.
2. 掌握圆周角定理的推论“在同圆或等圆中,同弧或等弧所对的圆周角相等,相等的圆周角所对的弧也相等”
3. 会运用上述圆周角定理的推论解决简单几何问题.
教学重点:圆周角定理的推论”在同圆或等圆中,同弧或等弧所对的圆周角相等,相等的圆周角所对的弧也相等”
教学难点:例3涉及圆内角与圆外角与圆周角的关系,思路较难形成,表述也有一定的困难
例4的辅助线的添法.
教学过程:
一、旧知回放:
1、圆周角定义: 顶点在圆上,并且两边都和圆相交的角叫圆周角.
特征:① 角的顶点在圆上.
② 角的两边都与圆相交.
2、圆心角与所对的弧的关系
3、圆周角与所对的弧的关系
4、同弧所对的圆心角与圆周角的关系
圆周角定理: 一条弧所对的圆周角等于它所对的圆心角的一半.
二. 课前测验
1.100 的弧所对的圆心角等于_______,所对的圆周角等于_______。
2、一弦分圆周角成两部分,其中一部分是另一部分的4倍,则这弦所对的圆周角度数为________________。
3、如图,在⊙O中,∠BAC=32 ,则∠BOC=________。
4、如图,⊙O中,∠ACB = 130 ,则∠AOB=______。
5、下列命题中是真命题的是( )
(A)顶点在圆周上的角叫做圆周角。
(B)60 的圆周角所对的弧的度数是30
(C)一弧所对的圆周角等于它所对的圆心角。
(D)120 的弧所对的圆周角是60
三, 问题讨论
如图1,在⊙O中,∠B,∠D,∠E的大小有什么关系 为什么
圆周角定理的推论1:同圆或等圆中,同弧或等弧所对的圆周角相等;
同圆或等圆中,相等的圆周角所对的弧也相等。
四.例题教学:
例2: 已知:如图,在△ABC中,AB=AC,
以AB为直径的圆交BC于D,交AC于E,
求证:⌒ ⌒
BD=DE
证明:连结AD.
∵AB是圆的直径,点D在圆上,
∴∠ADB=90°
∴AD⊥BC,
∵AB=AC,
∴AD平分顶角∠BAC,即∠BAD=∠CAD,
⌒ ⌒
∴BD=DE(同圆或等圆中,相等的圆周角所对弧相等)。
练习:如图,P是△ABC的外接圆上的一点∠APC=∠CPB=60°。
求证:△ABC是等边三角形
例3: 船在航行过程中,船长常常通过测定角度来确定是否会遇到暗礁。如图A,B表示灯塔,暗礁分布在经过A,B两点的一个圆形区域内,C表示一个危险临界点,∠ACB就是“危险角”,当船与两个灯塔的夹角大于“危险角”时,就有可能触礁。
问题:弓形所含的圆周角∠C=50°,问船在航行时怎样才能保证不进入暗礁区
(1)当船与两个灯塔的夹角∠α大于“危险角”时,船位于哪个区域?为什么?
(2)当船与两个灯塔的夹角∠α小于“危险角”时,船位于哪个区域?为什么?
五:练一练:
1.说出命题’圆的两条平行弦所夹的弧相等”的逆命题.原命题和逆命题都是真命题吗 请说明理由.
2.已知:四边形ABCD内接于圆,BD平分∠ABC,且AB∥CD.求证:AB=CD
六.想一想: 如图:AB是⊙O的直径,弦CD⊥AB于点E,G是⌒上任意一点,延长AG,与DC的延长线相交于点F,连接AD,GD,CG,找出图中所有
和∠ADC相等的角,并说明理由.
拓展练习:
1、已知BC为半圆O的直径,AB=AF,AC交BF于点M,过A点作AD⊥BC于D,交BF于E,则AE与BE的大小有什么关系?为什么?
七:小结: 1、本节课我们学习了哪些知识?
2、圆周角定理及其推论的用途你都知道了吗?
第10周第1课时上课时间10月30日(星期一)本学期累计教39个
课题:3.3圆心角和3.4圆周角练习课
一、填空题:
1.如图1,等边三角形ABC的三个顶点都在⊙O上,D是上任一点(不与A、C重合),则∠ADC的度数是________.毛
(1) (2) (3)
2.如图2,四边形ABCD的四个顶点都在⊙O上,且AD∥BC,对角线AC与BC相交于点E,那么图中有_________对相等的角。
3.已知,如图3,∠BAC的对角∠BAD=100°,则∠BOC=_______度.
4.如图4,A、B、C为⊙O上三点,若∠OAB=46°,则∠ACB=_______度.
(4) (5) (6)
5.如图5,AB是⊙O的直径, ,∠A=25°,则∠BOD的度数为________.
6.如图6,AB是半圆O的直径,AC=AD,OC=2,∠CAB= 30 °, 则点O 到CD 的距离OE=______.
二、选择题:
7.如图7,已知圆心角∠BOC=100°,则圆周角∠BAC的度数是( )
A.50° B.100° C.130° D.200°
(7) (8) (9) (10)
8.如图8,A、B、C、D四个点在同一个圆上,四边形ABCD 的对角线把四个内角分成的八个角中,相等的角有( )
A.2对 B.3对 C.4对 D.5对
9.如图9,D是的中点,则图中与∠ABD相等的角的个数是( )
A.4个 B.3个 C.2个 D.1个
10.如图10,∠AOB=100°,则∠A+∠B等于( )
A.100° B.80° C.50° D.40°
11.在半径为R的圆中有一条长度为R的弦,则该弦所对的圆周角的度数是( )
A.30° B.30°或150° C.60° D.60°或120°
12.如图,A、B、C三点都在⊙O上,点D是AB延长线上一点,∠AOC=140°, ∠CBD 的度数是( )
A.40° B.50° C.70° D.110°
三、解答题:
13.如图,⊙O的直径AB=8cm,∠CBD=30°,求弦DC的长.
14.如图,A、B、C、D四点都在⊙O上,AD是⊙O的直径,且AD=6cm,若∠ABC= ∠CAD,求弦AC的长.
15.如图,在⊙O中,AB是直径,CD是弦,AB⊥CD.
(1)P是上一点(不与C、D重合),试判断∠CPD与∠COB的大小关系, 并说明理由.
(2)点P′在劣弧CD上(不与C、D重合时),∠CP′D与∠COB有什么数量关系 请证明你的结论.
16.在足球比赛场上,甲、乙两名队员互相配合向对方球门MN进攻.当甲带球部到A点时,乙随后冲到B点,如图所示,此时甲是自己直接射门好,还是迅速将球回传给乙,让乙射门好呢 为什么 (不考虑其他因素)
17.钳工车间用圆钢做方形螺母,现要做边长为a的方形螺母, 问下料时至少要用直径多大的圆钢
答案:
1.120° 2.3 1 3.160° 4.44° 5.50° 6. 7.A 8.C 9.B 10.C 11.B 12.C
13.连接OC、OD,则OC=OD=4cm,∠COD=60°,故△COD是等边三角形,从而CD= 4cm.
14.连接DC,则∠ADC=∠ABC=∠CAD,故AC=CD.
∵AD是直径,∴∠ACD=90°, ∴AC2+CD2=AD2,即2AC2=36,AC2=18,AC=3.
15.(1)相等.理由如下:连接OD,∵AB⊥CD,AB是直径,
∴,∴∠COB= ∠DOB.
∵∠COD=2∠P,∴∠COB=∠P,即∠COB=∠CPD.
(2)∠CP′D+∠COB=180°.
理由如下:连接P′P,
则∠P′CD=∠P′PD,∠P′PC=∠P′DC.
∴∠P′CD+∠P′DC=∠P′PD+∠P′PC=∠CPD.
∴∠CP′D=180°-(∠P′CD+∠P′DC)=180°-∠CPD=180°-∠COB,
从而∠CP′D+∠COB=180°.
16.迅速回传乙,让乙射门较好,在不考虑其他因素的情况下, 如果两个点到球门的距离相差不大,要确定较好的射门位置,关键看这两个点各自对球门MN的张角的大小,当张角越大时,射中的机会就越大,如图所示,则∠A
17.a.毛
第10周第2课时上课时间10月31日(星期二)本学期累计教40个
课题:3.5弧长及扇形的面积(1)
教学目标:1、 经历探索弧长计算公式的过程
2、掌握弧长计算公式,并会应用公式解决问题。
教学重点:圆的弧长计算公式
教学难点:例1图形较为复杂,牵涉的知识点较多,并需添加辅助线,思路不易形成。
教学设计:
一、复习(圆周长)
已知⊙O半径为R,⊙O的周长C是多少?C=2πR
这里π=3.14159…,这个无限不循环的小数叫做圆周率.
由于生产、生活实际中常遇到有关弧的长度计算,那么怎样求一段弧的长度呢?
提出新问题:已知⊙O半径为R,求n°圆心角所对弧长.
二、探究新问题、归纳结论
教师组织学生探讨(因为问题并不难,学生完全可以自己研究得到公式).
研究步骤:
(1)圆周长C=2πR;
(2)1°圆心角所对弧长= ;
(3)n°圆心角所对的弧长是1°圆心角所对的弧长的n倍;
(4)n°圆心角所对弧长= .
归纳结论:若设⊙O半径为R, n°圆心角所对弧长l,则
(弧长公式)
(三)理解公式、区分概念
教师引导学生理解:
(1)在应用弧长公式 进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;
(2)公式可以理解记忆(即按照上面推导过程记忆);
(3)区分弧、弧的度数、弧长三概念.度数相等的弧,弧长不一定相等,弧长相等的弧也不一定是等孤,而只有在同圆或等圆中,才可能是等弧.
(四)初步应用
例1、填空:
(1)半径为3cm,120°的圆心角所对的弧长是_______cm;
(2)已知圆心角为150°,所对的弧长为20π,则圆的半径为_______;
(3)已知半径为3,则弧长为π的弧所对的圆心角为_______.
例2、例1 一段圆弧的公路弯道,圆弧的半径是2km,一辆汽车以每小时60km的速度通过弯道,需20秒.求弯道所对的圆心角的度数。(精确到0.1度)
分析:(1)对照弧长公式,那些量是直接已知的,哪个量是要求的?
(2)要求弯道所对圆心角的度数,应先求出什么?
解(略)
例3、 如图,BM是⊙O的直径,四边形ABMN是矩形,D是⊙O上的点,DC⊥AN,与AN交于点C,已知AC=15,⊙O的半径为R=30,求的长。
分析:(1)要求的长,关键是求出所对的圆心角∠BOD的大小。
(2)如何求∠BOD的大小呢?
(3)利用已知条件并通过添加辅助线,构造出△DOB来帮助解决。
课堂练习:作业题第4题
五、总结
知识:圆周长、弧长公式;圆周率概念;
能力:探究问题的方法和能力,弧长公式的记忆方法;初步应用弧长公式解决问题.
六、作业 作业本
第10周第3课时上课时间11月1日(星期三)本学期累计教41个
课题:3.5弧长及扇形的面积(2)
教学目标:1、经历探索扇形面积计算公式的过程;
2、掌握扇形面积的计算公式,并会应用公式解决问题。
教学重点:扇形面积的计算公式。
教学难点:例4涉及弓形面积的计算和流量与流速关系等实际背景,较为复杂。
教学设计:
一、复习圆面积
已知⊙O半径为R,⊙O的面积S是多少?(S=πR2)
我们在求面积时往往只需要求出圆的一部分面积,如图中阴影图形的面积.为了更好研究这样的图形引出一个概念.
扇形:一条弧和经过这条弧的端点的两条半径所组成的图形叫做扇形.
提出新问题:已知⊙O半径为R,求圆心角n°的扇形的面积.
二、探究问题、归纳结论
1、探究问题
教师组织学生对比研究:
(1)圆面积S=πR2;
(2)圆心角为1°的扇形的面积= ;
(3)圆心角为n°的扇形的面积是圆心角为1°的扇形的面积n倍;
(4)圆心角为n°的扇形的面积= .
2、归纳结论:若设⊙O半径为R,圆心角为n°的扇形的面积S扇形,则
S扇形= (扇形面积公式)
(三)理解公式
教师引导学生理解:
(1)在应用扇形的面积公式S扇形= 进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;
(2)公式可以理解记忆(即按照上面推导过程记忆);
提出问题:扇形的面积公式与弧长公式有联系吗?(教师组织学生探讨)
S扇形= lR
想一想:这个公式与什么公式类似?(教师引导学生进行,或小组协作研究)
与三角形的面积公式类似,只要把扇形看成一个曲边三角形,把弧长l看作底,R看作高就行了.这样对比,帮助学生记忆公式.实际上,把扇形的弧分得越来越小,作经过各分点的半径,并顺次连结各分点,得到越来越多的小三角形,那么扇形的面积就是这些小三角形面积和的极限.要让学生在理解的基础上记住公式.
(四)应用
(一)练习:1、已知扇形的圆心角为120°,半径为2,则这个扇形的面积S扇=____.
2、已知扇形面积为 ,圆心角为120°,则这个扇形的半径R=____.
3、已知半径为2的扇形,面积为 ,则它的圆心角的度数=____.
4、已知半径为2cm的扇形,其弧长为 ,则这个扇形的面积,S扇=____.
5、已知半径为2的扇形,面积为 ,则这个扇形的弧长=____.
小结:由上面练习题可知:在弧长、圆心角、半径、扇形面积四个量中只要知道其中的两个量就可以求出另外的两个量,但必须要知道圆的半径。
(二)例题
例3、如图,有一把折扇和一把团扇。已知折扇的骨柄与团扇的直径一样长,折扇扇面的宽度是骨柄长的一半,折扇张开的角度为120 °,问哪一把扇子扇面的面积大?
分析:折扇扇面的面积没有直接的公式可用,应该咋办?(转化为两个扇形的面积之差来计算。
例4、我国著名的引水工程的主干线输水管的直径为2.5m,设计流量为12.73m3 /s.如果水管截面中水面面积如图所示,其中∠AOB=45°,那么水的流速因达到多少m/s.
分析:(1)水的流速与水的流量、截面中水面的面积有什么关系?
(2) 截面中水面的面积即圆的面积与空隙部分弓形面积之差。
(3)弓形面积为扇形AOB与三角形AOB的差。
(三)课堂练习:课本第86页第4题.
五、总结
1、知识:扇形及扇形面积公式S扇形= ,S扇形= lR.
2、方法能力:迁移能力,对比方法;计算能力的培养.
六、作业 见作业本
第10周第4课时上课时间11月2日(星期四)本学期累计教案42个
课题:3.6圆锥的侧面积和全面积
教学目标:1、经历圆锥的侧面积计算公式的探索过程;
2、掌握圆锥的侧面积计算公式,会利用公式进行计算,并会解决实际问题;
3、让学生观察将圆锥的曲面展开在一个平面上的图形。回顾圆锥及其侧面积展开图之间的关系。
教学重点:圆锥侧面积的计算及计算公式
教学难点:圆锥侧面积计算公式的推导过程需要较强的空间想象能力。
教学设计:
[幻灯展示生活中常遇的圆锥形物体,如:铅锤、粮堆、烟囱帽]
前面屏幕上展示的物体都是什么几何体?
在小学我们已学过圆锥,哪位同学能说出圆锥有哪些特征?
答:圆锥是由一个底面和一个侧面围成的,圆锥的底面是一个圆,侧面是一个曲面,从圆锥的顶点到底面圆的距离是圆锥的高。
[教师边演示模型,边启发提问]:
1. 给一圆锥,如何找到它的母线?圆锥的母线应具有什么性质?
2. 现在我把这圆锥的侧面沿它的一条母线剪开,展在一个平面上,
这个展开图是什么图形?
3.圆锥展示图——扇形的弧长l等于圆锥底面圆的什么?
4.扇形的半径其实是圆锥的什么线段?
[扇形的弧长是底面圆的周长,即 ,扇形的半径。就是圆锥的母线]
由于 ,圆锥半径已知则展开图扇形的弧长已知,圆锥母线已知则展开图
扇形的半径已知,因此展开图扇形的面积可求,而这个扇形的面积实质就是圆锥的侧面积,因此圆锥的侧面积也就可求.当然展开图扇形的圆心角也可求.
例1: 圆锥形的烟囱帽的底面直径是80cm,母线长50cm,
计算烟囱帽侧面积.(取3.14,结果保留2个有效数字)
分析:此题直接根据公式,注意最后的答案要根据预定的精确度,用科学记数法写成含两个有效数字的表示形式)
练习:
1.如果圆锥底面半径为4cm,它的侧面积为 ,那么圆锥的母线长为_________.
2.圆锥的底面半径为2 cm,高为cm,则这个圆锥表面积_____________
3一个扇形,半径为30cm,圆心角为120度,用它做成一个圆锥的侧面,那么这个
圆锥的底面半径为_________________
4.圆锥的侧面积是底面积的2倍,这个圆锥的侧面展开图扇形的圆心角是__________
例2、已知一个圆锥的轴截面△ABC是等边三角形,它的表面积为75cm2,求这个圆锥的底面半径和母线的长。
分析:求有关底面半径、母线长、高往往要在直角三角形中
利用勾股定理求得,但此题中只知道表面积所以考虑用方程的思想。
练习:课本作业题的1、2、3
小结:请同学们回顾一下,本堂课我们学了些什么知识?
作业:见作业本
第10周第5课时上课时间11月3日(星期五)本学期累计教案43个
课题:“3.5弧长及扇形的面积、3.6 圆锥的侧面积和全面积”练习
(见实验检测八)
第11周第1课时上课时间11月6日(星期一)本学期累计教案44个
课题:第三章圆的基本性质 复习之一
教学目标:1、通过复习使学生系统掌握本章内容;
2、灵活应用圆的基本性质进行证明和计算。
教学重点和难点:灵活运用垂径定理和逆定理进行证明和计算。
教学设计:
一、知识要点:用填空形式进行(课前发给学生)
1、圆的确定:(1)圆心和半径;(2) 的三点确定一个圆。
2、 点与圆的三种位置关系:
若在平面内的一点P到半径为R的圆心O的距离为d,,则点P 在圆外 ;则点P 在圆上 ;则点P 在圆内 。
3、圆是轴对称图形,它的对称轴是 ,有 条。
4、圆是中心对称图形,对称中心是 ,圆具有绕其圆心旋转的 性。
5、垂径定理:垂直于弦的直径 这条弦, 弦所对的两条弧。
逆定理:平分弦(不是弦)的直径 ;平分弦所对的弧的直径 。
6、圆心角、弧、弦、弦心距之间的关系:在同圆或等圆中,如果 、
、 、 中有一组量相等,那么它们所对应的其余各组量都相等。
二、典型例题解析
例1、(1)下列命题中正确的是( )
A、 圆周角等于圆心角的一半; B、相等的圆周角所对的弧相等;
C、等弧所对的圆周角相等; D、任意三点可以确定一个圆。
(2)⊙O的半径为10 cm ,弦AB∥CD,阿布=12cm ,CD =16cm,则AB和CD的距离为( )
A、2cm B、14cm C、2cm或14cm D、10cm 或20cm
(3)如图,⊙O的直径为10,弦AB=8,P是弦AB上的一个动点,那么OP的长的取值范围是 。
(4)如果AB为⊙O的直径,弦CD⊥AB,垂足为E,那么下面结论中错误的是( )
A、CE=DE B、 C、∠BAC=∠BAD D、AC>AD
例2、
A
B
C
D
O
E
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
A
B
C
D
O
E
⌒
⌒
⌒
⌒
⌒
⌒
⌒
O
A
B
C
⌒
⌒
B
C
O
∠AOB=∠COD
AB=CD
OE=OF
AB=CD
⌒
⌒
O
C
B
A
A
C
O
A
A
B
C
D
A
B
D
G
F
C
E
O
同课章节目录
