2.1 二次函数[上学期]

课件18张PPT。2.1二次函数温十七中九年级数学备课组请用适当的函数解析式表示下列问题情境中
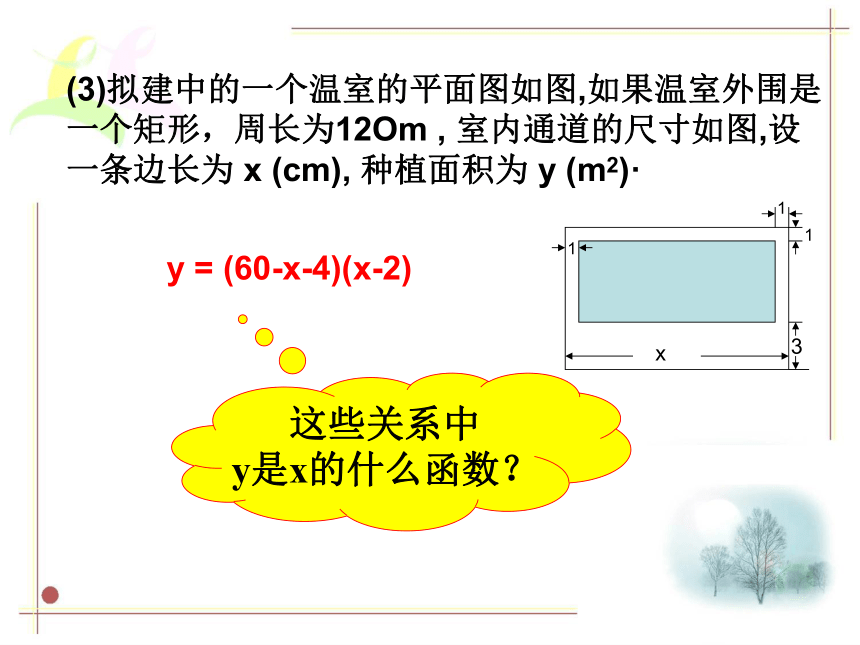
的两个变量 y 与 X 之间的关系·y =πx2(2)王先生存人银行2万元,先存一个一年定期，一年后银行将本息自动转存为又一个一年定期,设一年定期的年存款利率为文 x 两年后王先生共得本息y元;y = 2(1+x)2(3)拟建中的一个温室的平面图如图,如果温室外围是一个矩形，周长为12Om , 室内通道的尺寸如图,设一条边长为 x (cm), 种植面积为 y (m2)·y = (60-x-4)(x-2)这些关系中
y是x的什么函数？1、y =πx22、y = 2(1+x)23、y = (60-x-4)(x-2)=2x2+4x+2=-x2+58x-112上述三个问题中的函数解析式具有哪些共同的特征?经化简后都具y=ax2+bx+c 的形式.(a,b,c是常数, )a≠0 我们把形如y=ax2+bx+c
(其中a,b,C是常数，a≠0)的函数叫做二次函数(quadratic funcion) ,
称：a为二次项系数，
b为一次项系数，
c为常数项，例如，
1、二次函数 y=-x2+58x-112 的
二次项系数为 ，
一次项系数为 ，
常数项 。
2、二次涵数y=πx2的
二次项系 ,
一次项系数 ，
常数项 。a=-1b=58c=-112a=πb=0c=01.下列函数中,哪些是二次函数?做一做:是不是是是不是2、分别说出下列二次函数的二次项系数、
一次项系数和常数项：例：y=x2 + 2x – 3 我们把形如y=ax2+bx+c
(其中a,b,C是常数，a≠0)的函数叫做二次函数(quadratic funcion) ,
想一想:函数的自变量x是否可以取任何值呢?
注意:当二次函数表示某个实际问题时,还必须根据题意确定自变量的取值范围.
例1 如图， 一张正方形纸板的边长为2cm，
将它剪去4个全等 的直角三角形 (图中阴影部分 )·
设AE=BF=CG=DH=x(cm)，
四边形 EFGH的面积为y(cm2)，
求 :
(l) y关于 x的函数解析式和自变量x的取值池围 ;
(2 )当 x分别为0.25，0.5，1，1.5，1.75时 ，
对应的四边形 EFGH的 面积，并列表表示.
3. 用20米的篱笆围一个矩形的花圃（如图），设连墙的一边为x,矩形的面积为y,求：
(1)写出y关于x的函数关系式.
(2)当x=3时,矩形的面积为多少?（２）当x=3时(o 课本P 30---31 页作业题再见作业：m2-2二次函数？想一想:温馨提示：同桌交对，互相帮助！ 心理学家研究发现：一般情况下，学生的注意力随着教师讲课时间的变化而变化，讲课开始时，学生的注意力y随时间t的变化规律有如下关系式：（1）讲课开始后第5分钟时与讲课开始后第25分钟时比较，何时学生的注意力更集中？（2）讲课开始后多少分钟，学生的注意力最集中？能持续多少分钟？（3）一道数学难题，需要讲解24分钟，为了效果较好，要求学生的注意力最低达到180，那么经过适当安排，老师能否在学生注意力达到所需的状态下讲解完这道题目？