二次函数复习[上学期]

课件16张PPT。　二次函数
·二次函数 的概念
·二次函数的图象特点
·二次函数的性质
·题型分析
形如y＝ax2＋bx＋c （a、b、c是常数，a≠0）的函数叫做x的二次函数 。如：
y＝－x2， y＝2x2－4x＋3 ， y＝100－5x2，
－2x2＋5x－3 。1.什么叫二次函数 ?
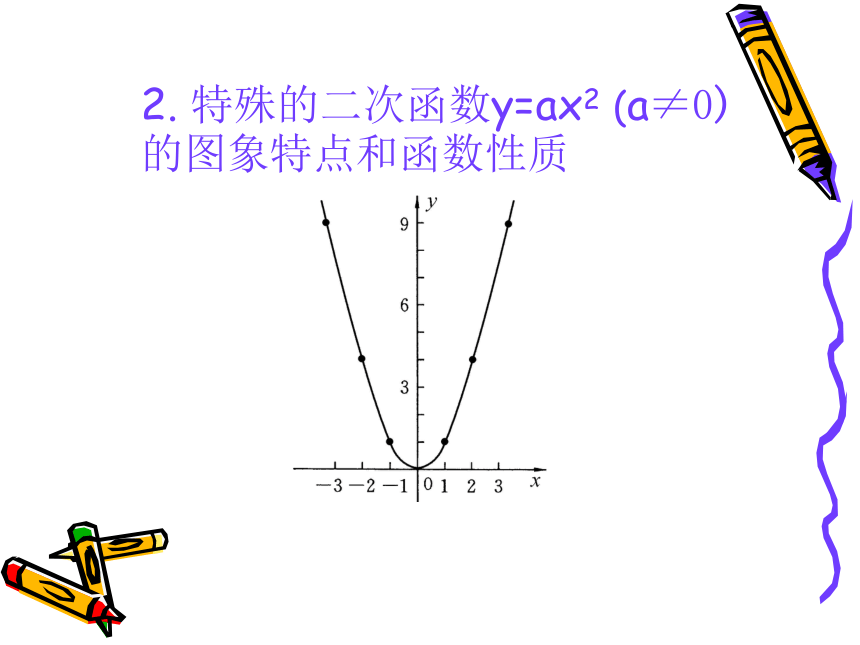
2. 特殊的二次函数y=ax2 (a≠0)的图象特点和函数性质
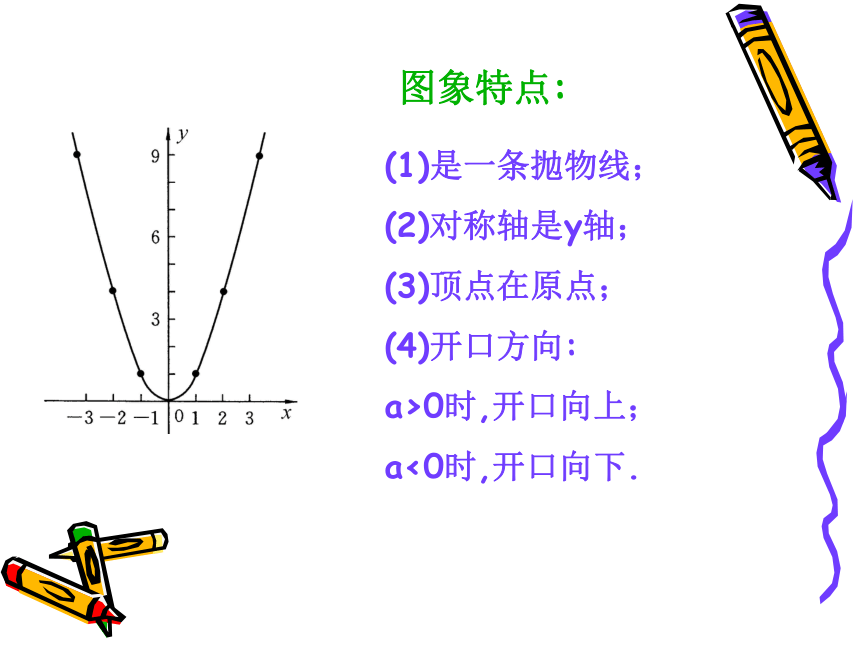
(1)是一条抛物线；
(2)对称轴是y轴；
(3)顶点在原点；
(4)开口方向:
a>0时,开口向上；
a<0时,开口向下.
图象特点:
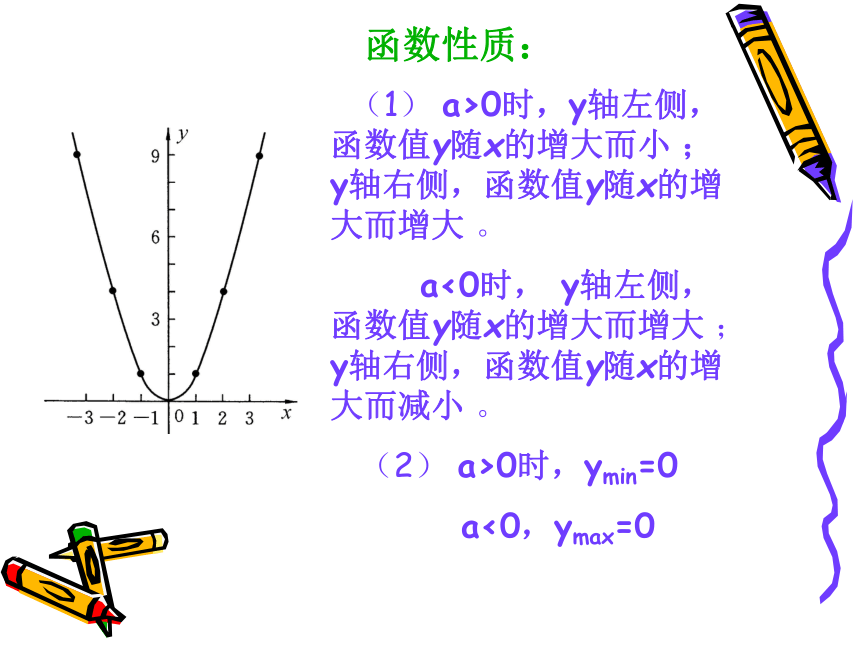
（1） a>0时，y轴左侧，函数值y随x的增大而小 ； y轴右侧，函数值y随x的增大而增大 。
a<0时， y轴左侧，函数值y随x的增大而增大 ； y轴右侧，函数值y随x的增大而减小 。
（2） a>0时，ymin=0
a<0，ymax=0
函数性质：3.一般二次函数 y=ax2+bx+c(a≠0)的图象特点和函数性质
(1)是一条抛物线；
(2)对称轴是:x=-
(3)顶点坐标是:(- , )
(4)开口方向:
a>0时,开口向上；
a<0时,开口向下.
图象特点:
（1） a>0时，对称轴左侧(x<- )，函数值y随x的增大而减小 ；对称轴右侧(x>- )，函数值y随x的增大而增大 。
a<0时，对称轴左侧(x<- )，函数值y随x的增大而增大 ；对称轴右侧(x>- )，函数值y随x的增大而减小 。
（2） a>0时，ymin=
a<0时，ymax=
函数性质：题型分析:
(一)抛物线与x轴、y轴的交点急所构成的面积
例1:填空：
(1)抛物线y＝x2－3x＋2与y轴的交点坐标是____________，与x轴的交点坐标是____________；
(2)抛物线y＝－2x2＋5x－3与y轴的交点坐标是____________，与x轴的交点坐标是____________． (0,2)(1,0)和(2,0)(0,-3)例2:已知抛物线y=x2-2x-8，（1）求证：该抛物线与x轴一定有两个交点；（2）若该抛物线与x轴的两个交点分别为A、B，且它的顶点为P，求△ABP的面积。 例3:在同一直角坐标系中，一次函数y=ax+c和二次函数y=ax2+c的图象大致为
(二)根据函数性质判定函数图象之间的位置关系答案: B(三)由函数图象上的点的坐标求函数解析式例4:已知一个二次函数的图象经过点（0，0），（1，﹣3），（2，﹣8）。
（1）求这个二次函数的解析式；
（2）写出它的对称轴和顶点坐标。
答案:(1)y=-x2-2x
(2)对称轴:x=-1
顶点坐标(-1,1)例5:已知二次函数y=x2－mx－4．设该函数的图象
与x轴的交点坐标为(x1，O)、(x2，O)，且,求m的值，并求出该函数图象的顶点坐标．(四)二次函数与一元二次方程综合题例6:某企业投资100万元引进一条产品加工生产线，若不计维修、保养费用，预计投产后每年可创利33万。该生产线投产后，从第1年到第x年的维修、保养费用累计为y(万元)，且y=ax2+bx,若第1年的维修、保养 费用为2万元，第2年为6万元。
　　（1）求y的解析式；
　　（2）投产后，这个企业在第几年就能收回投资？解:（1）由题意，x=1时，y=2；x=2时，y=2+4=6,分别代入y=ax2+bx,得a+b=2,4a+2b=6,
解得:a=1,b=1, ∴y=x2+x.
　　（2）设g＝33x-100-x2-x,则
　　g=-x2+32x-100=-(x-16)2+156.
由于当1≤x≤16时，g随x的增大而增大，故当x=4时，即第4年可收回投资。(五)实践与探索题练习题:1.已知二次函数的图象的顶点坐标为（－2，－3），且图象过点（－3，－2）。（1）求此二次函数的解析式；（2）设此二次函数的图象与x轴交于A，B两点，O为坐标原点，求线段OA，OB的长度之和。2.已知抛物线与x轴交于B，A两点，其中B在x轴的负半轴上，点A在x轴的正半轴上，该抛物线与y轴交于点C.
（1）写出抛物线的开口方向与点C的坐标（用含m的式子表示）；
（2）若tg∠CBA=3，试求抛物线的解析式；
（3）设点P（x，y）（其中0＜x＜3＝是（2）中抛物线上的一个动点，试求四边形AOCP的面积的最大值及此时点P的坐标.