浙教版2022年九年级上册第4章《相似三角形》单元检测卷 (含解析)
文档属性
| 名称 | 浙教版2022年九年级上册第4章《相似三角形》单元检测卷 (含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 743.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-21 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
浙教版2022年九年级上册第4章《相似三角形》单元检测卷
一.选择题(共10小题,满分30分,每小题3分)
1.已知线段a,b,c,求作线段x,使bx=ac,下列作法中正确的是( )
A. B.
C. D.
2.如果x:y=2:3,那么下列各式中成立的是( )
A. B.2x=3y C. D.
3.如图所示的两个五边形相似,则以下a,b,c,d的值错误的是( )
A.a=3 B.b=4.5 C.c=4 D.d=8
4.已知△ABC∽△DEF,AG和DH是它们的对应边上的高,若AG=4,DH=6,则△ABC与△DEF的面积比是( )
A.2:3 B.4:9 C.3:2 D.9:4
5.如图,在△ABC中,P为AB上一点,在下列四个条件中,不能判定△APC和△ACB相似的条件是( )
A.∠ACP=∠B B.∠APC=∠ACB
C.AC2=AP AB D.AC CP=AP CB
6.如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,则下列结论不正确的是( )
A. B.
C.△ADE∽△ABC D.AD AB=AE AC
7.如图所示,在平面直角坐标系中,A(1,0),B(0,2),C(﹣2,1),以A为位似中心,把△ABC在点A同侧按相似比1:2放大,放大后的图形记作△A'B'C',则C'的坐标为( )
A.(﹣6,2) B.(﹣5,2) C.(﹣4,2) D.(﹣3,2)
8.将两张直角三角形纸片按如图所示的方式摆进⊙O内,点A,B,C,D都在圆上,点E在边AC上,已知∠BAC=∠AED=90°,AB=AE=6,DE=2,则⊙O的直径为( )
A. B. C. D.10
9.已知点P是边长为4的正方形ABCD内一点,且PB=3,BF⊥BP,垂足是点B,若在射线BF上找一点M,使以点B,M,C为顶点的三角形与△ABP相似,则BM为( )
A.3 B. C.3 或 D.以上都错
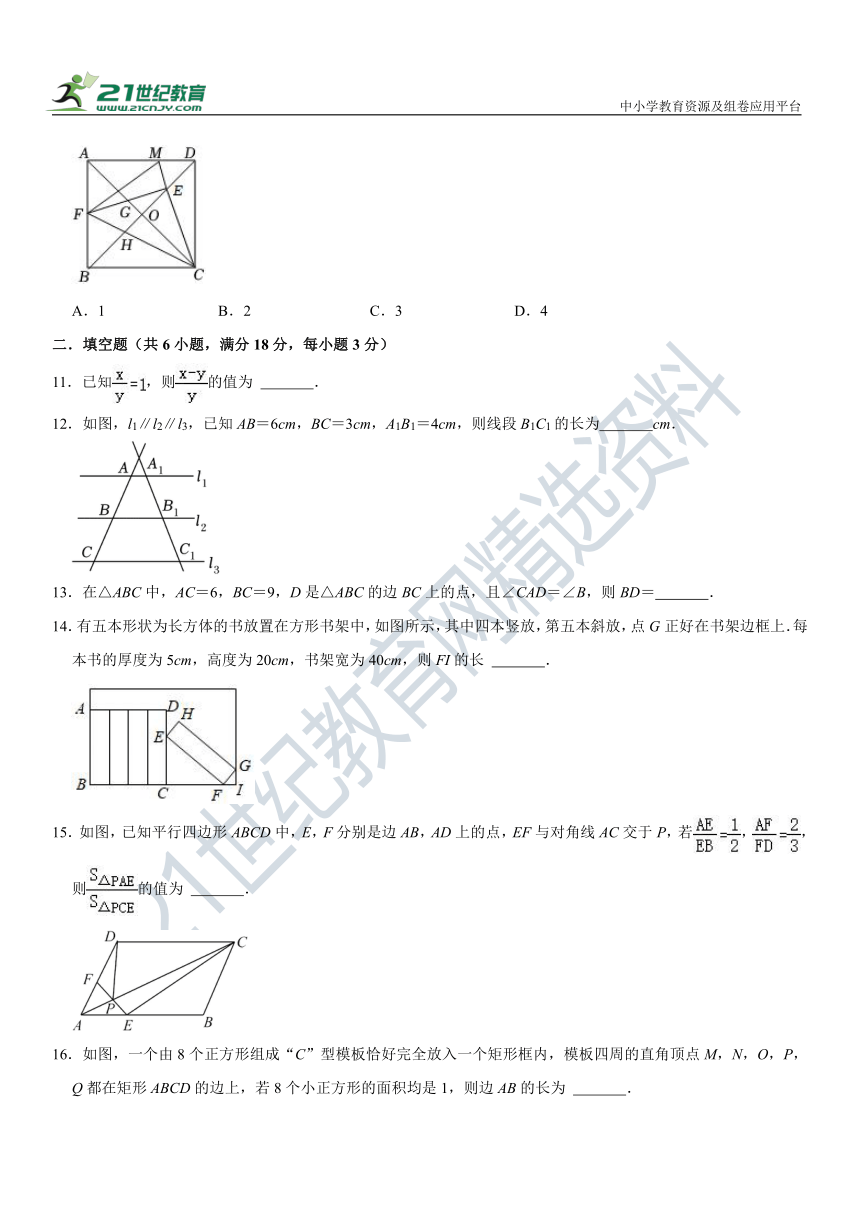
10.如图,在边长为4的正方形ABCD中,对角线AC,BD交于点O,E在BD上,连接CE,作EF⊥CE交AB于点F,交AC于点G,连接CF交BD于点H,延长CE交AD于点M,连接FM,则下列结论:①点E到AB,BC的距离相等;②∠FCE=45°;③∠DMC=∠FMC;④若DM=2,则.正确的有( )个.
A.1 B.2 C.3 D.4
二.填空题(共6小题,满分18分,每小题3分)
11.已知,则的值为 .
12.如图,l1∥l2∥l3,已知AB=6cm,BC=3cm,A1B1=4cm,则线段B1C1的长为 cm.
13.在△ABC中,AC=6,BC=9,D是△ABC的边BC上的点,且∠CAD=∠B,则BD= .
14.有五本形状为长方体的书放置在方形书架中,如图所示,其中四本竖放,第五本斜放,点G正好在书架边框上.每本书的厚度为5cm,高度为20cm,书架宽为40cm,则FI的长 .
15.如图,已知平行四边形ABCD中,E,F分别是边AB,AD上的点,EF与对角线AC交于P,若,,则的值为 .
16.如图,一个由8个正方形组成“C”型模板恰好完全放入一个矩形框内,模板四周的直角顶点M,N,O,P,Q都在矩形ABCD的边上,若8个小正方形的面积均是1,则边AB的长为 .
三.解答题(共7小题,满分52分)
17.(6分)如图,在△ABC中,BD平分∠ABC,交AC于点D,点E是AB上一点,连接DE,BD2=BC BE.证明:△BCD∽△BDE.
18.(6分)某校初三年级在一次研学活动中,数学研学小组为了估计澧水河某段水域的宽度,在河的对岸选定一个目标点A,在近岸分别取点B、D、E、C,使点A、B、D在一条直线上,且AD⊥DE,点A、C、E也在一条直线上,且DE∥BC.经测量BC=25米,BD=12米,DE=35米,求河的宽度AB为多少米?
19.(7分)已知线段a,b,c满足a:b:c=2:3:4,且a+b﹣c=3.
(1)求线段a,b,c的长.
(2)若线段m是线段a,b的比例中项,求线段m的长.
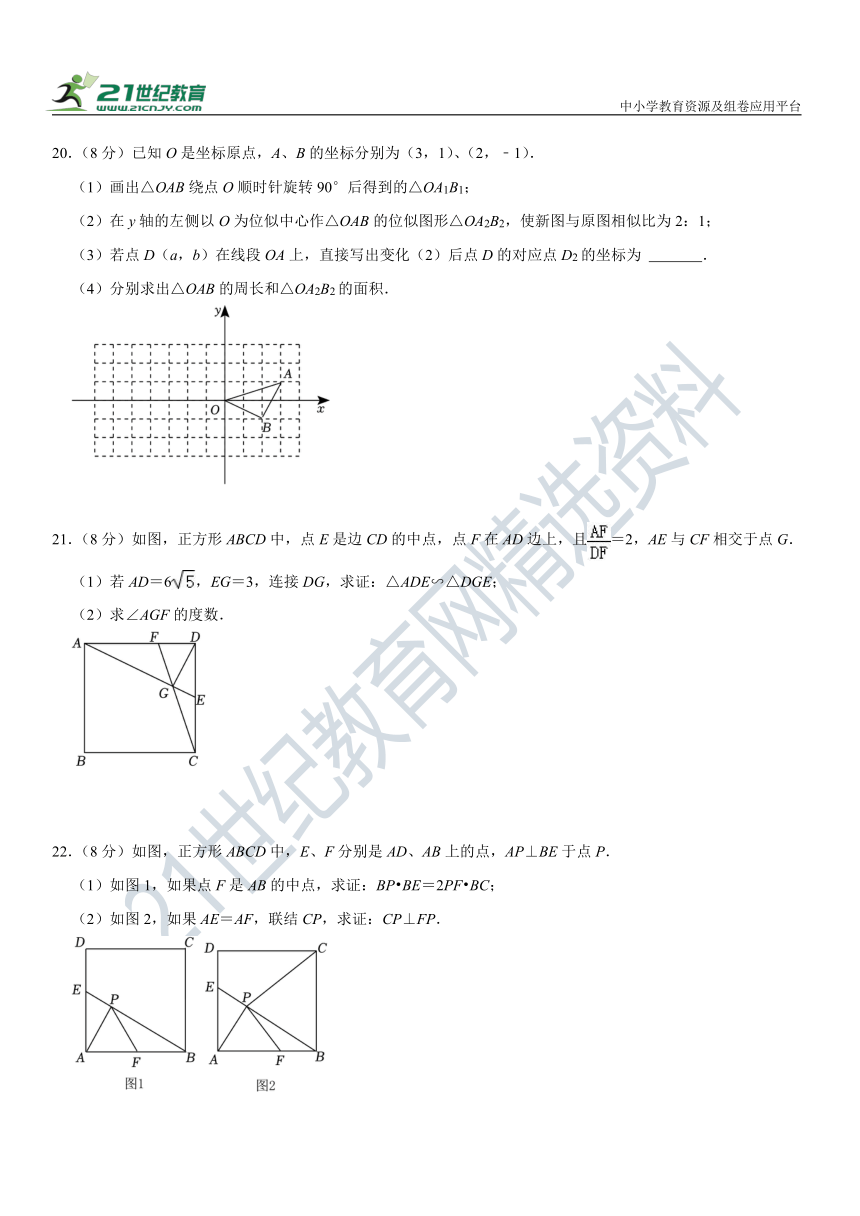
20.(8分)已知O是坐标原点,A、B的坐标分别为(3,1)、(2,﹣1).
(1)画出△OAB绕点O顺时针旋转90°后得到的△OA1B1;
(2)在y轴的左侧以O为位似中心作△OAB的位似图形△OA2B2,使新图与原图相似比为2:1;
(3)若点D(a,b)在线段OA上,直接写出变化(2)后点D的对应点D2的坐标为 .
(4)分别求出△OAB的周长和△OA2B2的面积.
21.(8分)如图,正方形ABCD中,点E是边CD的中点,点F在AD边上,且=2,AE与CF相交于点G.
(1)若AD=6,EG=3,连接DG,求证:△ADE∽△DGE;
(2)求∠AGF的度数.
22.(8分)如图,正方形ABCD中,E、F分别是AD、AB上的点,AP⊥BE于点P.
(1)如图1,如果点F是AB的中点,求证:BP BE=2PF BC;
(2)如图2,如果AE=AF,联结CP,求证:CP⊥FP.
23.(9分)如图,在矩形ABCD中,AB=6,AD=8,点E是CD边上的一个动点(点E不与点C重合),延长DC到点F,使EC=2CF,且AF与BE交于点G.
(1)当EC=4时,求线段BG的长;
(2)设CF=x,△GEF的面积为y,求y与x的关系式,并求出y的最大值;
(3)连接DG,求线段DG的最小值.
浙教版2022年九年级上册第4章《相似三角形》单元检测卷
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.【解答】解:由题意,bx=ac,
∴=,
故选:D.
2.【解答】解:∵x:y=2:3,
∴设x=2k,y=3k,
A、==﹣,故本选项不符合题意;
B、∵x:y=2:3,∴3x=2y,故本选项不符合题意;
C、∵x:y=2:3,∴=,故本选项,符合题意;
D、不能约分,故本选项不符合题意.
故选:C.
3.【解答】解:∵两个五边形相似,
∴====,
∴a=3,b=4.5,c=4,d=6.
故选:D.
4.【解答】解:∵△ABC∽△DEF,AG和DH是它们的对应边上的高,
∴=()2=()2=,
故选:B.
5.【解答】解:当∠ACP=∠B时,∵∠A=∠A,
∴△ACP∽∠ABC;
当∠APC=∠ACB时,∵∠A=∠A,
∴△ACP∽∠ABC;
当AC2=AP AB时,即,
∵A=∠A,
∴△ACP∽∠ABC;
当AB CP=AP CB时,即,
∵A=∠A,
∴不能判定△APC和△ACB相似,
故选:D.
6.【解答】解:∵DE∥BC,
∴△ADE∽△ABC,
∴==,
∴,
故选:D.
7.【解答】解:∵以A为位似中心,把△ABC按相似比1:2放大,放大后的图形记作△AB'C',
∴AC=AC′,
∴点C是线段AC′的中点,
∵A(1,0),C(﹣2,1),
∴C'的坐标为'(﹣5,2).
故选:B.
8.【解答】解:连接BD,CD,
∵圆周角∠BAC=90°,
∴BC是⊙O的直径,
∴∠BDC=90°,
设CE=a,由勾股定理得:AD===2,CD===,BC===,
∵∠DEA=∠BDC=90°,∠DBC=∠DAE(在同圆中,同弧所对的圆周角相等),
∴△AED∽△BDC,
∴=,
∴=,
解得:a=﹣或a=,
∵a表示边的长度,不能为负,
∴a=﹣舍去,
∴BC==,
即⊙O的直径是,
故选:A.
9.【解答】解:∵四边形ABCD是正方形,
∴∠ABC=90°,AB=BC=4,
又∵∠PBF=90°,
∴∠ABP=∠CBF=90°﹣∠CBP;
若以点B,M,C为顶点的三角形与△ABP相似,
则:①如图1中,,即=,解得BM=;
②如图2中,,即=,解得BM=3.
综上所述,满足条件的BM的值为3或.
故选:C.
10.【解答】解:如图,连接AE,设FM交AC于点I,
∵四边形ABCD是正方形,
∴AB=AD=CB=CD,∠BAD=∠BCD=∠ABC=90°,
∴∠ABD=∠ADB=45°,∠CBD=∠CDB=45°,
∴∠ABD=∠CBD,
∴点E到AB,BC的距离相等,
故①正确;
在△ABE和△CBE中,
,
∴△ABE≌△CBE(SAS),
∴AE=CE,∠BAE=∠BCE,
∵EF⊥CE,
∴∠CEF=∠MEF=90°,
∴∠BCE+∠BFE=180°,
∵∠EFA+∠BFE=180°,
∴∠BCE=∠EFA,
∴∠BAE=∠EFA,
∴AE=FE,
∴CE=FE,
∴∠FCE=∠CFE=45°,
故②正确;
∵AD∥BC,
∴∠DME=∠BCE=∠BAE,
∵∠MDE=∠ABE,
∴△MDE∽△ABE,
∴=,
∴=,
∵∠MEF=∠MDC,
∴△MEF∽△MDC,
∴∠DMC=∠FMC,
故③正确;
作FL⊥BD于点L,则∠BLF=90°,设BL=x,
∴∠LFB=∠LBF=45°,
∴FL=BL=x,
∵BF2=BL2+FL2=2BL2,
∴BF=x,
∵AD=CD=BC=4,DM=2,
∴CM==2,BD==4,
∵△DEM∽△BEC,
∴====,
∴FE=CE=CM=,BE=BD=,
∵EL===,
∴x+=,
解得x1=,x2=2(不符合题意,舍去),
∴BF=×=≠,
故④错误,
故选:C.
二.填空题(共6小题,满分18分,每小题3分)
11.【解答】解:∵=1,
∴x=y,
∴==0.
故答案为:0.
12.【解答】解:∵l1∥l2∥l3,
∴,
∴AB=6cm,BC=3cm,A1B1=4cm,
∴,
解得B1C1=2.
故答案为:2.
13.【解答】解:∵∠CAD=∠B,∠C=∠C,
∴△DAC∽△ABC,
∴=,
∵AC=6,BC=9,
∴=,
∴DC=4,
∴BD=BC﹣DC=9﹣4=5,
故答案为:5.
14.【解答】解:由题知,CI=BI﹣BC=40﹣20=20cm,EF=20cm,FG=5cm,
∵∠EFC+∠CEF=90°,∠EFC+∠GFI=90°,
∴∠CEF=∠GFI,
∵∠ECF=∠FIG=90°,
∴△GIF∽△FEC,
∴=,
即=,
∴CE=4FI,
在Rt△CEF中,由勾股定理得CE2+CF2=EF2,
即(4FI)2+(20﹣FI)2=202,
解得FI=或FI=0(舍去),
故答案为:cm.
15.【解答】解:过E作EH∥AD,交DC于点H,交AC于点G,如图:
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴EH∥BC,
∴==,
∴设AG=a,GC=2a,
∵DC∥AB,
∴△CHG∽△AEG,
∴==,
∴=,
∴EG=EH,
∵=,
∴=,,
∴AF=AD=EH,
∵AD∥EH,
∴AF∥EG,
∴△APF∽△GPE,
∴===,
∴AP=a,PG=,
∴PC=a,
∴=,
故答案为:.
16.【解答】解:如图所示,连接EG,则∠OEP=90°,
由题意得,小正方形的边长为1,
∴OP==,
∵四边形ABCD是矩形,
∴∠B=∠C=∠A=90°,∠MQP=90°,
∴∠BMQ=∠CQP=90°﹣∠MQP,
同理∠EPO=∠CQP=90°﹣∠QPC,
∴∠BMQ=∠EPO,
又∠OEP=∠B=90°,
∴△OEP∽△QBM,
∴===,
∴BM===,QB===,
∵∠B=∠A=90°,∠NMQ=90°,
∴∠BMQ=∠ANM=90°﹣∠AMN,
在△QBM和△MAN中,
,
∴△QBM≌△MAN(AAS),
∴AM=QB=,
∴AB=BM+AM=.
故答案为:.
三.解答题(共7小题,满分52分)
17.【解答】证明:∵BD平分∠ABC,
∴∠DBE=∠CBD.
∵BD2=BC BE,
∴,
∴△BCD∽△BDE.
18.【解答】解:∵BC∥DE,
∴△ABC∽△ADE,
∴=,
即=,
∴AB=30.
答:河的宽度AB为30米.
19.【解答】解:(1)∵a:b:c=2:3:4,
∴a=2k,b=3k,c=4k,
∵a+b﹣c=3,
∴2k+3k﹣4k=3,
解得k=3,
∴a=6,b=9,c=12;
(2)∵m是a、b的比例中项,
∴m2=ab,
∴m2=6×9,
∴x=3或x=﹣3(舍去),
即线段m的长为3.
20.【解答】解:(1)如图所示:△OA1B1即为所求;
(2)如图所示:△OA2B2即为所求;
(3)∵点D(a,b)
∴变化(2)后点D的对应点D2的坐标为(﹣2a,﹣2b),
故答案为:(﹣2a,﹣2b);
(4)△OAB的周长=++=+,△OA2B2的面积=×5×(2+2)=10.
21.【解答】(1)证明:∵四边形ABCD是正方形,AD=6,点E是边CD的中点,
∴DE=3,
∴AE==15,
∵EG=3,
∴=,,
∴,
∵∠AED=∠DEG,
∴△ADE∽△DGE;
(2)连接AC,过F作FH⊥AC,垂足为点H,
设AD=3a,则AF=2a,DF=a,DE=a,
∵四边形ABCD是正方形,
∴∠CAD=45°,AC=3a,AE=,
∴△AHF是等腰直角三角形,
∴AH=FH=a,CH=2a,
∴=2,=2,
∴,
∵∠CHF=∠ADE=90°,
∴△CHF∽△ADE,
∴∠HCF=∠DAE,
∵∠AGF=∠GAC+∠ACG,
∴∠AGF=∠GAC+∠DAE=∠CAD=45°.
22.【解答】证明:(1)如图1,∵四边形ABCD是正方形,
∴∠BAE=90°,
∵AP⊥BE,
∴∠BPA=90°,
∴∠BPA=∠BAE,
∵∠PBA=∠ABE,
∴△BPA∽△BAE,
∴=,
∵点F是AB的中点,
∴BA=2PF,
∵BA=BC,
∴=,
∴BP BE=2PF BC.
(2)∵△BPA∽△BAE,
∴=,
∴=,
∴AE=AF,BA=BC,
∴=,
∵BC∥AD,
∴∠CBP=∠BEA,
∵∠BEA=∠FAP,
∴∠CBP=∠FAP,
∴△CBP∽△FAP,
∴∠BPC=∠APF,
∴∠FPC=∠BPF+∠BPC=∠BPF+∠APF=∠BPA=90°,
∴CP⊥FP.
23.【解答】解:(1)当EC=4时,则:
CF=2,
∴AB=FE=6,
∵四边形ABCD为矩形,
∴AB∥CD,
∴∠F=∠BAG,∠ABG=∠FEG,
∴△ABG≌△FEG(ASA),
∴BG=EG=BE,
在直角三角形BCE中,BC=8,CE=4,
∴BE=4,
∴BG=2;
(2)如图,过点G作MN∥AD分别交AB,CD于点M,N,
设CF=x,则:
EF=3x,
显然△ABG∽△FEG,
∴=,
设GN=h,则:
MG=8﹣h,
∴===,
∴h=,
∴S△GEF=y=×3x×=,
∴y与x的关系式为:y=,
∵x>0,2x≤6,
∴0<x≤3,
∵y==,
∴y随x的增加而增加,
∴当x=3时,ymax=;
(3)如图,在AB上取一点Q,使得BQ=2AQ,
∵AB∥CD,
∴△AQG∽△FCG,△BQG∽△DCG,
∴==,==,
∴点E在CD上运动总会有=,即
点G在线段CQ上运动,
∴当点E与点D重合时,CG最长,
∵=,
∴GC=,
如图,作DM⊥CQ,GN⊥CD,当点G运动到点M时,此时DG即为最小值,
∵DM CG=CD GN,
∴DM =×6×(×8),
∴DM=,
∴DG的最小值为.
浙教版2022年九年级上册第4章《相似三角形》单元检测卷
一.选择题(共10小题,满分30分,每小题3分)
1.已知线段a,b,c,求作线段x,使bx=ac,下列作法中正确的是( )
A. B.
C. D.
2.如果x:y=2:3,那么下列各式中成立的是( )
A. B.2x=3y C. D.
3.如图所示的两个五边形相似,则以下a,b,c,d的值错误的是( )
A.a=3 B.b=4.5 C.c=4 D.d=8
4.已知△ABC∽△DEF,AG和DH是它们的对应边上的高,若AG=4,DH=6,则△ABC与△DEF的面积比是( )
A.2:3 B.4:9 C.3:2 D.9:4
5.如图,在△ABC中,P为AB上一点,在下列四个条件中,不能判定△APC和△ACB相似的条件是( )
A.∠ACP=∠B B.∠APC=∠ACB
C.AC2=AP AB D.AC CP=AP CB
6.如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,则下列结论不正确的是( )
A. B.
C.△ADE∽△ABC D.AD AB=AE AC
7.如图所示,在平面直角坐标系中,A(1,0),B(0,2),C(﹣2,1),以A为位似中心,把△ABC在点A同侧按相似比1:2放大,放大后的图形记作△A'B'C',则C'的坐标为( )
A.(﹣6,2) B.(﹣5,2) C.(﹣4,2) D.(﹣3,2)
8.将两张直角三角形纸片按如图所示的方式摆进⊙O内,点A,B,C,D都在圆上,点E在边AC上,已知∠BAC=∠AED=90°,AB=AE=6,DE=2,则⊙O的直径为( )
A. B. C. D.10
9.已知点P是边长为4的正方形ABCD内一点,且PB=3,BF⊥BP,垂足是点B,若在射线BF上找一点M,使以点B,M,C为顶点的三角形与△ABP相似,则BM为( )
A.3 B. C.3 或 D.以上都错
10.如图,在边长为4的正方形ABCD中,对角线AC,BD交于点O,E在BD上,连接CE,作EF⊥CE交AB于点F,交AC于点G,连接CF交BD于点H,延长CE交AD于点M,连接FM,则下列结论:①点E到AB,BC的距离相等;②∠FCE=45°;③∠DMC=∠FMC;④若DM=2,则.正确的有( )个.
A.1 B.2 C.3 D.4
二.填空题(共6小题,满分18分,每小题3分)
11.已知,则的值为 .
12.如图,l1∥l2∥l3,已知AB=6cm,BC=3cm,A1B1=4cm,则线段B1C1的长为 cm.
13.在△ABC中,AC=6,BC=9,D是△ABC的边BC上的点,且∠CAD=∠B,则BD= .
14.有五本形状为长方体的书放置在方形书架中,如图所示,其中四本竖放,第五本斜放,点G正好在书架边框上.每本书的厚度为5cm,高度为20cm,书架宽为40cm,则FI的长 .
15.如图,已知平行四边形ABCD中,E,F分别是边AB,AD上的点,EF与对角线AC交于P,若,,则的值为 .
16.如图,一个由8个正方形组成“C”型模板恰好完全放入一个矩形框内,模板四周的直角顶点M,N,O,P,Q都在矩形ABCD的边上,若8个小正方形的面积均是1,则边AB的长为 .
三.解答题(共7小题,满分52分)
17.(6分)如图,在△ABC中,BD平分∠ABC,交AC于点D,点E是AB上一点,连接DE,BD2=BC BE.证明:△BCD∽△BDE.
18.(6分)某校初三年级在一次研学活动中,数学研学小组为了估计澧水河某段水域的宽度,在河的对岸选定一个目标点A,在近岸分别取点B、D、E、C,使点A、B、D在一条直线上,且AD⊥DE,点A、C、E也在一条直线上,且DE∥BC.经测量BC=25米,BD=12米,DE=35米,求河的宽度AB为多少米?
19.(7分)已知线段a,b,c满足a:b:c=2:3:4,且a+b﹣c=3.
(1)求线段a,b,c的长.
(2)若线段m是线段a,b的比例中项,求线段m的长.
20.(8分)已知O是坐标原点,A、B的坐标分别为(3,1)、(2,﹣1).
(1)画出△OAB绕点O顺时针旋转90°后得到的△OA1B1;
(2)在y轴的左侧以O为位似中心作△OAB的位似图形△OA2B2,使新图与原图相似比为2:1;
(3)若点D(a,b)在线段OA上,直接写出变化(2)后点D的对应点D2的坐标为 .
(4)分别求出△OAB的周长和△OA2B2的面积.
21.(8分)如图,正方形ABCD中,点E是边CD的中点,点F在AD边上,且=2,AE与CF相交于点G.
(1)若AD=6,EG=3,连接DG,求证:△ADE∽△DGE;
(2)求∠AGF的度数.
22.(8分)如图,正方形ABCD中,E、F分别是AD、AB上的点,AP⊥BE于点P.
(1)如图1,如果点F是AB的中点,求证:BP BE=2PF BC;
(2)如图2,如果AE=AF,联结CP,求证:CP⊥FP.
23.(9分)如图,在矩形ABCD中,AB=6,AD=8,点E是CD边上的一个动点(点E不与点C重合),延长DC到点F,使EC=2CF,且AF与BE交于点G.
(1)当EC=4时,求线段BG的长;
(2)设CF=x,△GEF的面积为y,求y与x的关系式,并求出y的最大值;
(3)连接DG,求线段DG的最小值.
浙教版2022年九年级上册第4章《相似三角形》单元检测卷
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.【解答】解:由题意,bx=ac,
∴=,
故选:D.
2.【解答】解:∵x:y=2:3,
∴设x=2k,y=3k,
A、==﹣,故本选项不符合题意;
B、∵x:y=2:3,∴3x=2y,故本选项不符合题意;
C、∵x:y=2:3,∴=,故本选项,符合题意;
D、不能约分,故本选项不符合题意.
故选:C.
3.【解答】解:∵两个五边形相似,
∴====,
∴a=3,b=4.5,c=4,d=6.
故选:D.
4.【解答】解:∵△ABC∽△DEF,AG和DH是它们的对应边上的高,
∴=()2=()2=,
故选:B.
5.【解答】解:当∠ACP=∠B时,∵∠A=∠A,
∴△ACP∽∠ABC;
当∠APC=∠ACB时,∵∠A=∠A,
∴△ACP∽∠ABC;
当AC2=AP AB时,即,
∵A=∠A,
∴△ACP∽∠ABC;
当AB CP=AP CB时,即,
∵A=∠A,
∴不能判定△APC和△ACB相似,
故选:D.
6.【解答】解:∵DE∥BC,
∴△ADE∽△ABC,
∴==,
∴,
故选:D.
7.【解答】解:∵以A为位似中心,把△ABC按相似比1:2放大,放大后的图形记作△AB'C',
∴AC=AC′,
∴点C是线段AC′的中点,
∵A(1,0),C(﹣2,1),
∴C'的坐标为'(﹣5,2).
故选:B.
8.【解答】解:连接BD,CD,
∵圆周角∠BAC=90°,
∴BC是⊙O的直径,
∴∠BDC=90°,
设CE=a,由勾股定理得:AD===2,CD===,BC===,
∵∠DEA=∠BDC=90°,∠DBC=∠DAE(在同圆中,同弧所对的圆周角相等),
∴△AED∽△BDC,
∴=,
∴=,
解得:a=﹣或a=,
∵a表示边的长度,不能为负,
∴a=﹣舍去,
∴BC==,
即⊙O的直径是,
故选:A.
9.【解答】解:∵四边形ABCD是正方形,
∴∠ABC=90°,AB=BC=4,
又∵∠PBF=90°,
∴∠ABP=∠CBF=90°﹣∠CBP;
若以点B,M,C为顶点的三角形与△ABP相似,
则:①如图1中,,即=,解得BM=;
②如图2中,,即=,解得BM=3.
综上所述,满足条件的BM的值为3或.
故选:C.
10.【解答】解:如图,连接AE,设FM交AC于点I,
∵四边形ABCD是正方形,
∴AB=AD=CB=CD,∠BAD=∠BCD=∠ABC=90°,
∴∠ABD=∠ADB=45°,∠CBD=∠CDB=45°,
∴∠ABD=∠CBD,
∴点E到AB,BC的距离相等,
故①正确;
在△ABE和△CBE中,
,
∴△ABE≌△CBE(SAS),
∴AE=CE,∠BAE=∠BCE,
∵EF⊥CE,
∴∠CEF=∠MEF=90°,
∴∠BCE+∠BFE=180°,
∵∠EFA+∠BFE=180°,
∴∠BCE=∠EFA,
∴∠BAE=∠EFA,
∴AE=FE,
∴CE=FE,
∴∠FCE=∠CFE=45°,
故②正确;
∵AD∥BC,
∴∠DME=∠BCE=∠BAE,
∵∠MDE=∠ABE,
∴△MDE∽△ABE,
∴=,
∴=,
∵∠MEF=∠MDC,
∴△MEF∽△MDC,
∴∠DMC=∠FMC,
故③正确;
作FL⊥BD于点L,则∠BLF=90°,设BL=x,
∴∠LFB=∠LBF=45°,
∴FL=BL=x,
∵BF2=BL2+FL2=2BL2,
∴BF=x,
∵AD=CD=BC=4,DM=2,
∴CM==2,BD==4,
∵△DEM∽△BEC,
∴====,
∴FE=CE=CM=,BE=BD=,
∵EL===,
∴x+=,
解得x1=,x2=2(不符合题意,舍去),
∴BF=×=≠,
故④错误,
故选:C.
二.填空题(共6小题,满分18分,每小题3分)
11.【解答】解:∵=1,
∴x=y,
∴==0.
故答案为:0.
12.【解答】解:∵l1∥l2∥l3,
∴,
∴AB=6cm,BC=3cm,A1B1=4cm,
∴,
解得B1C1=2.
故答案为:2.
13.【解答】解:∵∠CAD=∠B,∠C=∠C,
∴△DAC∽△ABC,
∴=,
∵AC=6,BC=9,
∴=,
∴DC=4,
∴BD=BC﹣DC=9﹣4=5,
故答案为:5.
14.【解答】解:由题知,CI=BI﹣BC=40﹣20=20cm,EF=20cm,FG=5cm,
∵∠EFC+∠CEF=90°,∠EFC+∠GFI=90°,
∴∠CEF=∠GFI,
∵∠ECF=∠FIG=90°,
∴△GIF∽△FEC,
∴=,
即=,
∴CE=4FI,
在Rt△CEF中,由勾股定理得CE2+CF2=EF2,
即(4FI)2+(20﹣FI)2=202,
解得FI=或FI=0(舍去),
故答案为:cm.
15.【解答】解:过E作EH∥AD,交DC于点H,交AC于点G,如图:
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴EH∥BC,
∴==,
∴设AG=a,GC=2a,
∵DC∥AB,
∴△CHG∽△AEG,
∴==,
∴=,
∴EG=EH,
∵=,
∴=,,
∴AF=AD=EH,
∵AD∥EH,
∴AF∥EG,
∴△APF∽△GPE,
∴===,
∴AP=a,PG=,
∴PC=a,
∴=,
故答案为:.
16.【解答】解:如图所示,连接EG,则∠OEP=90°,
由题意得,小正方形的边长为1,
∴OP==,
∵四边形ABCD是矩形,
∴∠B=∠C=∠A=90°,∠MQP=90°,
∴∠BMQ=∠CQP=90°﹣∠MQP,
同理∠EPO=∠CQP=90°﹣∠QPC,
∴∠BMQ=∠EPO,
又∠OEP=∠B=90°,
∴△OEP∽△QBM,
∴===,
∴BM===,QB===,
∵∠B=∠A=90°,∠NMQ=90°,
∴∠BMQ=∠ANM=90°﹣∠AMN,
在△QBM和△MAN中,
,
∴△QBM≌△MAN(AAS),
∴AM=QB=,
∴AB=BM+AM=.
故答案为:.
三.解答题(共7小题,满分52分)
17.【解答】证明:∵BD平分∠ABC,
∴∠DBE=∠CBD.
∵BD2=BC BE,
∴,
∴△BCD∽△BDE.
18.【解答】解:∵BC∥DE,
∴△ABC∽△ADE,
∴=,
即=,
∴AB=30.
答:河的宽度AB为30米.
19.【解答】解:(1)∵a:b:c=2:3:4,
∴a=2k,b=3k,c=4k,
∵a+b﹣c=3,
∴2k+3k﹣4k=3,
解得k=3,
∴a=6,b=9,c=12;
(2)∵m是a、b的比例中项,
∴m2=ab,
∴m2=6×9,
∴x=3或x=﹣3(舍去),
即线段m的长为3.
20.【解答】解:(1)如图所示:△OA1B1即为所求;
(2)如图所示:△OA2B2即为所求;
(3)∵点D(a,b)
∴变化(2)后点D的对应点D2的坐标为(﹣2a,﹣2b),
故答案为:(﹣2a,﹣2b);
(4)△OAB的周长=++=+,△OA2B2的面积=×5×(2+2)=10.
21.【解答】(1)证明:∵四边形ABCD是正方形,AD=6,点E是边CD的中点,
∴DE=3,
∴AE==15,
∵EG=3,
∴=,,
∴,
∵∠AED=∠DEG,
∴△ADE∽△DGE;
(2)连接AC,过F作FH⊥AC,垂足为点H,
设AD=3a,则AF=2a,DF=a,DE=a,
∵四边形ABCD是正方形,
∴∠CAD=45°,AC=3a,AE=,
∴△AHF是等腰直角三角形,
∴AH=FH=a,CH=2a,
∴=2,=2,
∴,
∵∠CHF=∠ADE=90°,
∴△CHF∽△ADE,
∴∠HCF=∠DAE,
∵∠AGF=∠GAC+∠ACG,
∴∠AGF=∠GAC+∠DAE=∠CAD=45°.
22.【解答】证明:(1)如图1,∵四边形ABCD是正方形,
∴∠BAE=90°,
∵AP⊥BE,
∴∠BPA=90°,
∴∠BPA=∠BAE,
∵∠PBA=∠ABE,
∴△BPA∽△BAE,
∴=,
∵点F是AB的中点,
∴BA=2PF,
∵BA=BC,
∴=,
∴BP BE=2PF BC.
(2)∵△BPA∽△BAE,
∴=,
∴=,
∴AE=AF,BA=BC,
∴=,
∵BC∥AD,
∴∠CBP=∠BEA,
∵∠BEA=∠FAP,
∴∠CBP=∠FAP,
∴△CBP∽△FAP,
∴∠BPC=∠APF,
∴∠FPC=∠BPF+∠BPC=∠BPF+∠APF=∠BPA=90°,
∴CP⊥FP.
23.【解答】解:(1)当EC=4时,则:
CF=2,
∴AB=FE=6,
∵四边形ABCD为矩形,
∴AB∥CD,
∴∠F=∠BAG,∠ABG=∠FEG,
∴△ABG≌△FEG(ASA),
∴BG=EG=BE,
在直角三角形BCE中,BC=8,CE=4,
∴BE=4,
∴BG=2;
(2)如图,过点G作MN∥AD分别交AB,CD于点M,N,
设CF=x,则:
EF=3x,
显然△ABG∽△FEG,
∴=,
设GN=h,则:
MG=8﹣h,
∴===,
∴h=,
∴S△GEF=y=×3x×=,
∴y与x的关系式为:y=,
∵x>0,2x≤6,
∴0<x≤3,
∵y==,
∴y随x的增加而增加,
∴当x=3时,ymax=;
(3)如图,在AB上取一点Q,使得BQ=2AQ,
∵AB∥CD,
∴△AQG∽△FCG,△BQG∽△DCG,
∴==,==,
∴点E在CD上运动总会有=,即
点G在线段CQ上运动,
∴当点E与点D重合时,CG最长,
∵=,
∴GC=,
如图,作DM⊥CQ,GN⊥CD,当点G运动到点M时,此时DG即为最小值,
∵DM CG=CD GN,
∴DM =×6×(×8),
∴DM=,
∴DG的最小值为.
同课章节目录
