2.2 二次函数的图象(3)[上学期]
文档属性
| 名称 | 2.2 二次函数的图象(3)[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 714.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-04-12 07:30:00 | ||
图片预览



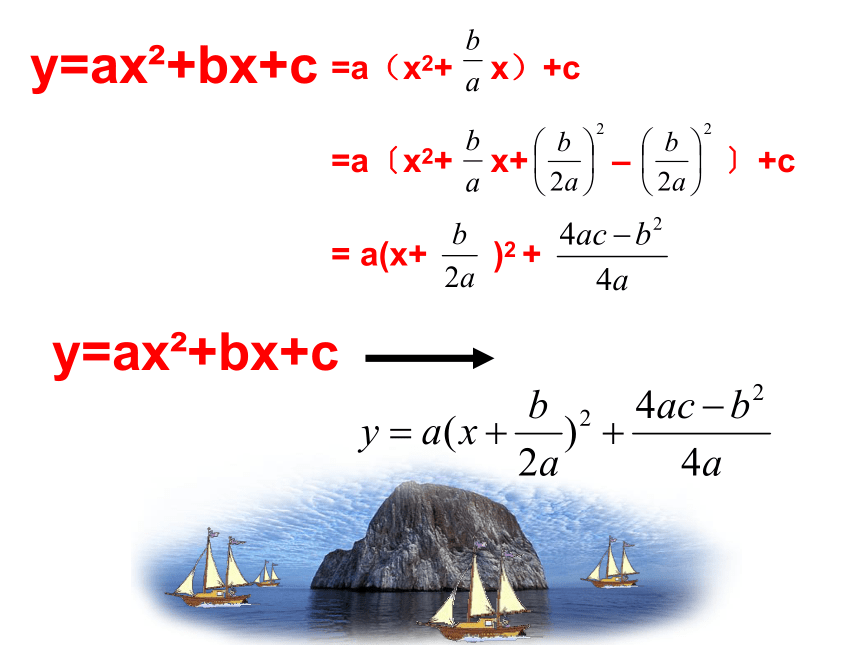



文档简介
课件14张PPT。2.2 二次函数的图象(3)时,图象将发生怎样的变化?二次函数y=ax2y = a(x+m)2y = a(x+m)2 +k1、顶点坐标?(0,0)(–m,0)( –m,k )2、对称轴?y轴(直线x=0)(直线x= –m )(直线x= –m )3、平移问题?一般地,函数y=ax2的图象先向右(当m<0)或向左 (当m>0)平移|m|个单位可得y = a(x+m)2的图象;若再向上(当k>0 )或向下 (当k<0 )平移|k|个单位可得到y = a(x+m)2 +k的图象。
对于二次函数y=ax2+bx+c ( a≠0 )的图象及图象的形状、开口方向、位置又是怎样的?通过变形能否将y=ax2+bx+c转化为
y = a(x+m)2 +k的形式 ?y=ax2+bx+c y=ax2+bx+c y=ax2+bx+c当a>0时,抛物线的开口向上,顶点是抛物线上的最低点。
当a<0时,抛物线的开口向下,顶点是抛物线上的最高点。解:因此,抛物线的对称轴是直线x=3,顶点坐标是(3,2)。1.说出下列抛物线的开口方向、顶点坐标和对称轴:做一做:开口方向:顶点坐标:对称轴:1、求下列函数图象的对称轴和顶点坐标:例5:已知二次函数y= x2+4x–3,
请回答下列问题:画函数图象2、说出函数图象的开口方向、对称轴
和顶点坐标。2. 说出下列函数的图象可由怎样的抛物线y=ax2(a≠0),经过怎样的平移后得到?.3、请写出如图所示的抛物线的解析式: (0,1)(2,4)xyO
一座拱桥的示意图如图,当水面宽12m时,桥洞顶部
离水面4m。已知桥洞的拱形是抛物线,要求该抛物线
的函数解析式,你认为首先要做的工作是什么?如果以
水平方向为x轴,取以下三个不同的点为坐标原点:1、点A 2、点B 3、抛物线的顶点C
所得的函数解析式相同吗?
请试一试。哪一种取法求
得的函数解析式最简单? 探究活动:ABC4m12m这节课你有什么收获和体会?
课本P 38页作业题及作业本作业:
对于二次函数y=ax2+bx+c ( a≠0 )的图象及图象的形状、开口方向、位置又是怎样的?通过变形能否将y=ax2+bx+c转化为
y = a(x+m)2 +k的形式 ?y=ax2+bx+c y=ax2+bx+c y=ax2+bx+c当a>0时,抛物线的开口向上,顶点是抛物线上的最低点。
当a<0时,抛物线的开口向下,顶点是抛物线上的最高点。解:因此,抛物线的对称轴是直线x=3,顶点坐标是(3,2)。1.说出下列抛物线的开口方向、顶点坐标和对称轴:做一做:开口方向:顶点坐标:对称轴:1、求下列函数图象的对称轴和顶点坐标:例5:已知二次函数y= x2+4x–3,
请回答下列问题:画函数图象2、说出函数图象的开口方向、对称轴
和顶点坐标。2. 说出下列函数的图象可由怎样的抛物线y=ax2(a≠0),经过怎样的平移后得到?.3、请写出如图所示的抛物线的解析式: (0,1)(2,4)xyO
一座拱桥的示意图如图,当水面宽12m时,桥洞顶部
离水面4m。已知桥洞的拱形是抛物线,要求该抛物线
的函数解析式,你认为首先要做的工作是什么?如果以
水平方向为x轴,取以下三个不同的点为坐标原点:1、点A 2、点B 3、抛物线的顶点C
所得的函数解析式相同吗?
请试一试。哪一种取法求
得的函数解析式最简单? 探究活动:ABC4m12m这节课你有什么收获和体会?
课本P 38页作业题及作业本作业:
同课章节目录
