2.4二次函数的应用（1）[上学期]

课件13张PPT。2.4 二次函数的应用⑴萧山区所前镇初中夏忠晓
浙教版九年级上册第二章二次函数一、教学目标：知识与技能目标：
①理解二次函数模型的基本构成（函数解析式、自变量的取值范围、函数的图像等）；
②会用二次函数求实际问题中的最大值或最小值；过程性（程序性）目标：
①使学生在“感受问题情境、数学活动、数学应用、回顾反思”的过程中，经历数学建模的基本过程；
②使学生在主动联系自己生活经历的过程中，体会到二次函数是一类最优化问题的重要数学模型，从而感受数学（函数）的应用价值；情感与价值观目标：
①使学生在经历数学建模的过程中培养“应用数学”的意识；
②使学生领会函数关系也正是揭示了现实世界不同数量间动态联系的规律，培养学生运用辩证与联系的观点看待问题。二、教学重点与难点：二次函数在最优化问题的应用回顾与练习1、求下列二次函数的最大值或最小值：
⑴ y=－x2＋58x－112; ⑵ y=－x2＋4x解： ⑴配方得： y=－(x－29)2＋729所以：当x=29时，y 达到最大值为729又因为： －1＜0，则：图像开口向下，⑵ －1＜0，
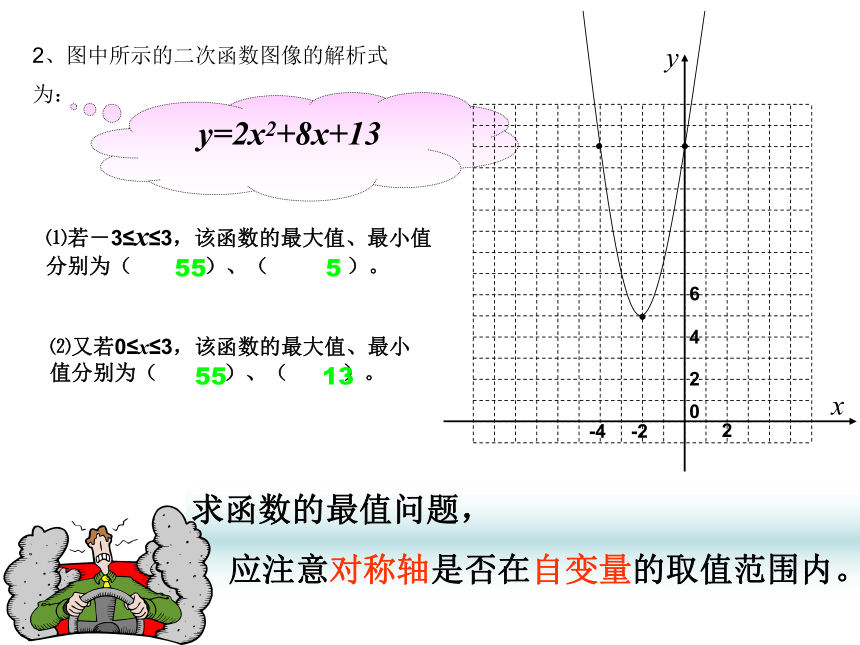
则：图像开口向下，函数有最大值所以由求最值公式可知，当x=2时， y达到最大值为4.2、图中所示的二次函数图像的解析式
为：
y=2x2+8x+13⑴若－3≤x≤3，该函数的最大值、最小值分别为（ ）、（ ）。 ⑵又若0≤x≤3，该函数的最大值、最小值分别为（ ）、（ ）。求函数的最值问题，
应注意对称轴是否在自变量的取值范围内。55 555 13情景建模问题：2、用长为8米的铝合金制成如图窗框，问窗框的宽和高各为多少米时，窗户的透光面积最大？最大面积是多少？解：设窗框的一边长为x米，
则另一边的长为（4－x）米，又令该窗框的透光面积为y米2，那么：y= x(4－x)且0＜ x＜4又有：－1＜0，
则：该函数的图像开口向下，故函数有最大值而图像的对称轴为直线x=2，且0＜ 2＜4即：y=－x2＋4x所以由求最值公式可知，当 x=2时，该函数达到最大值为4.答：该窗框的宽和高相等，都为2米时透光面积达到最大的4米2练习感悟⑴数据（常量、变量）提取；⑵自变量、应变量识别；⑶构建函数解析式，并求出自变量的取值范围；⑷利用函数（或图像）的性质求最大（或最小）值。探究与建模3.图中窗户边框的上部分是由4个全等扇形组成的半圆,下部分是矩形.如果制作一个窗户边框的材料的总长度为8米,那么如何设计这个窗户边框的尺寸,使透光面积最大?(结果精确到0.01米)解:设半圆的半径为r米，如图，矩形的一边长为l米，根据题意，有：5r+πr+2r+2l=8,即：l=4－0.5(π+7)r又因为：l＞0且r ＞0所以： 4－0.5(π+7)r＞0则：0＜r＜(0＜r＜ )归纳与小结对问题情景中的数量
（提取常量、变量）关系进行梳理；建立函数模型（求出解析式及相应自变量的取值范围等）
，解决问题。关于函数建模问题？用字母（参数）来表示不同数量
（如不同长度的线段）间的大小联系；1.如图，隧道横截面的下部是矩形，上部是半圆，周长为16米。（P45，第4题）
⑴求截面积S（米2）关于底部宽x（米）的函数解析式，及自变量x 的取值范围？
⑵试问：当底部宽x为几米时，隧道的截面积S最大（结果精确到0.01米）？变式与拓展2.已知，直角三角形的两直角边的和为2，求斜边长可能达到的最小值，以及当斜边长达到最小值时两条直角边的长。（P45，第2题）2.解：设其中的一条直角边长为x，
则另一条直角边长为（2－x）， 又设斜边长为y，
则：所以：当x＝1时，斜边长有最小值 ,
此时两条直角边的长均为11.解：∵隧道的底部宽为x，周长为16，答：当隧道的底部宽度为4.48米时，隧道的截面积最大。作业
1.教材P45，2、3、5；
2.浙教版配套作业本课时作业