2.3 二次函数的性质[上学期]

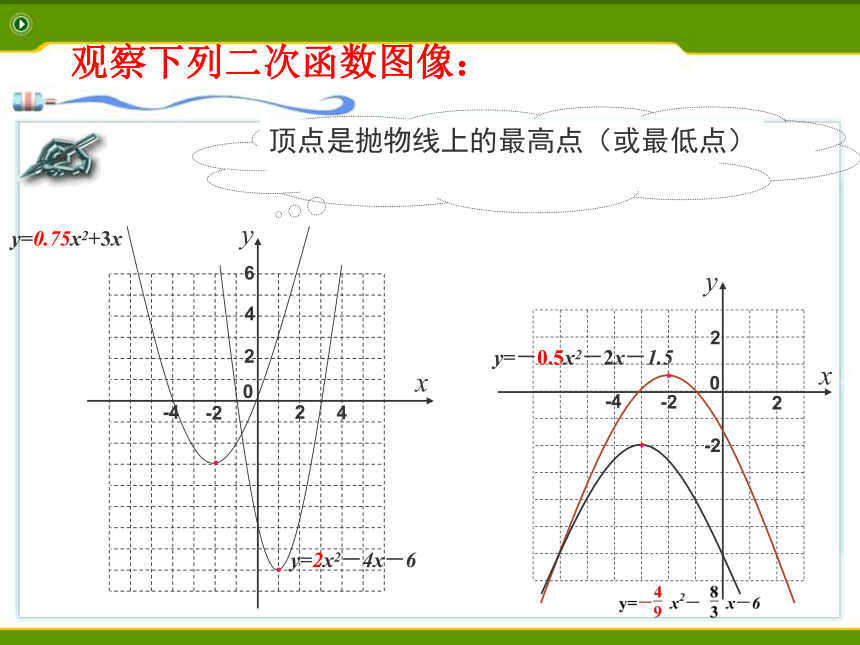
课件15张PPT。一枚普通的炮弹，无风状态下在空中运动的路线是一条怎样的曲线？怎样计算炮弹达到最高点时的高度？所前镇中：夏忠晓函数 y=ax2+bx+c基本性质回顾二次函数y=ax2+bx+c（a≠0）的图像是一条抛物线，观察下列二次函数图像：顶点在图像的位置有什么特点？顶点是抛物线上的最高点（或最低点）问：当自变量增大时，函数的值将怎样变化？你还能发现：
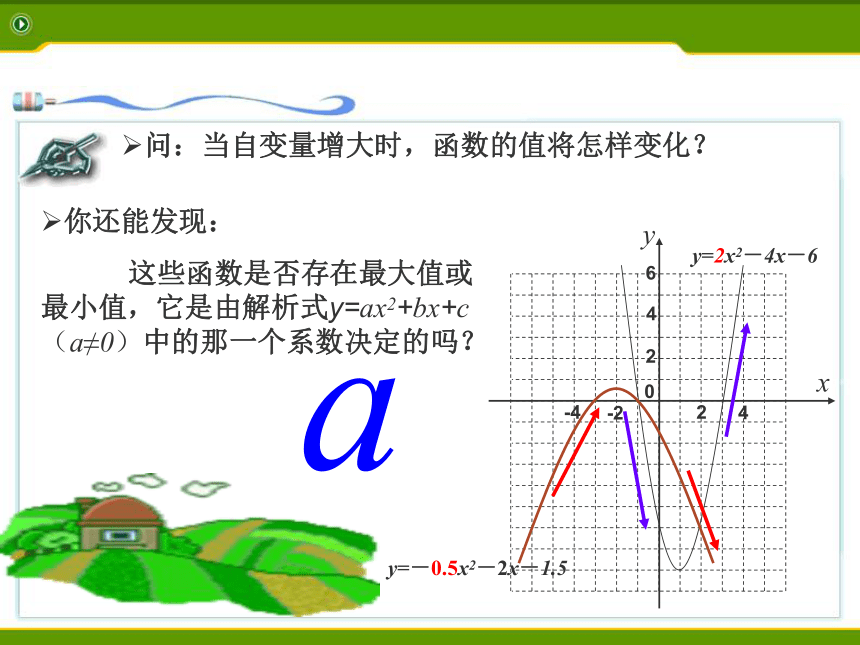
这些函数是否存在最大值或最小值，它是由解析式y=ax2+bx+c（a≠0）中的那一个系数决定的吗？a二次函数y=ax2+bx+c
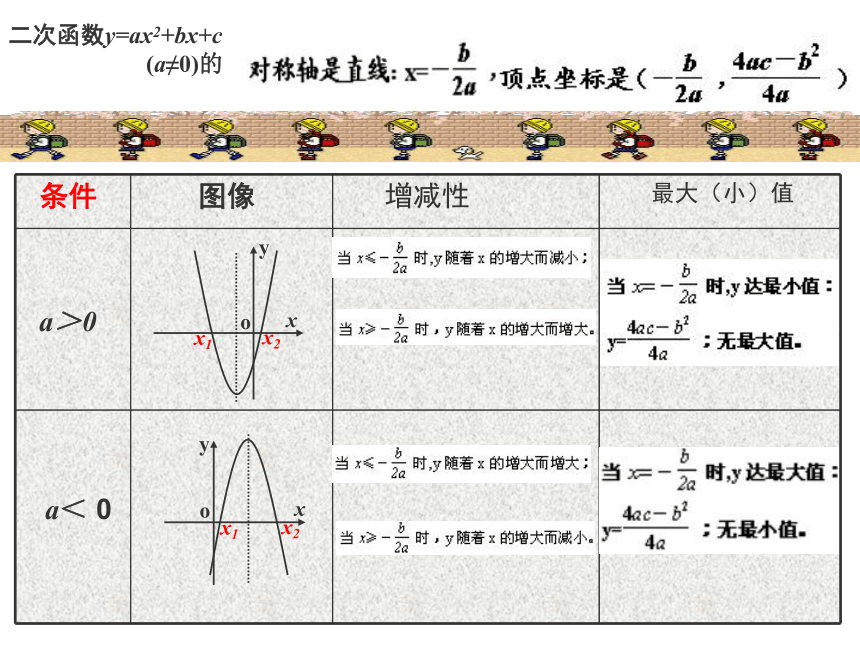
(a≠0)的
a＞0a＜ 0想一想 如果二次函数y=ax2+bx+c (a≠0)的图像与x轴的两个交点的
坐标为 （ x1，0 ）和（ x2 ，0）方程ax2+bx+c＝0 (a≠0)的解与二次函数y=ax2+bx+c (a≠0)的图像与x轴交点的坐标有什么关系？那么x1和 x2 恰好是方程ax2+bx+c＝0 (a≠0)的两个根方程ax2+bx+c＝0 (a≠0)的解就是
函数y=ax2+bx+c (a≠0)的图像与x轴交点的 坐标。横可以发现：二次函数y=ax2+bx+c (a≠0)的图像与x轴交点的 存在性与 方程ax2+bx+c＝0 (a≠0)的解是否存在有关。归纳与探究那么，进一步推想方程ax2+bx+c＝0 (a≠0)解的存在性又与什么有关呢？b2 －4ac的正负性有关。故而：
①当b2 －4ac 时，抛物线与x轴有 交点；②当b2 －4ac 时，抛物线与x轴只有 交点；③当b2 －4ac 时，抛物线与x轴 交点。＞0 两个＝0 一个＜0 没有太高兴，我懂啦！例题探究解：（1）∵a=－0.5,b=－7,c=7.5;所以函数y=－0.5x2－7x＋7.5的大致图像如图：⑵自变量x在什么范围内时，y随x 的增大而增大？何时y 随x的增大而减小？并求出函数的最大值或最小值。解： ⑵由右图可知，
当x≤－7时， y随x 的增大而增大；当x≥－7 时，y 随x的增大而减小；当x＝－7时，函数有最大值32。课内练习解： ⑴ ∵y=2x2－8x＋1＝2(x－2)2－7∴当x=2时,y有最小值,为－7⑵ ∵a=－3＞0且b=－5,c=1;
故:当x= 时，y有最 值，为大配方法公式法2、已知函数y=x2－3x－4.
⑴求函数图像的顶点坐标、与坐标轴交点的坐标和对称轴，并画出函数的大致图像；解：∵ y=x2－3x－4 ＝(x－1.5)2－6.25,
∴图象顶点坐标为(1.5, －6.25);又当y=0时，
得x2－3x－4＝0的解为：
x1＝－1，x2＝4。
则与x轴的交点为(－1,0)和(4,0) 与y轴的交点为(0, －4)⑵记当x1=3.5,x2= ,x3= 时对应的函数值分别为y1,y2,y3,试比较y1,y2,y3的大小?解:⑵如右图可知:
y2＞ y1 ＞ y3大家应该很好的利用二次函数图像给我们的启迪，来解决诸多问题！拓展与实践⑴球运动路线的函数解析式和自变量的取值范围；⑵球在运动中离地面的最大高度。解: ⑴设函数解析式为:
y=a(x－2.5)2+k,根据题意，得：则：a=－0.2,k=3.5∴解析式为:y=－0.2x2+x+2.25,
自变量x的取值范围为：0≤x≤4.⑵球在运动中离地面的最大高度
为3.5米。篮球运动员投篮时，球运动的路线为抛物线的一部分（如图），抛物线的对称轴为x=2.5。求：
再见