二次函数[上学期]
图片预览







文档简介
课件23张PPT。 二次函数复习
形如y=ax2+bx+c (a、b、c是常数,a≠0)的函数叫做x的二次函数 。二次函数的定义
说出下列二次函数的各项系数:
y=-x2
y=2(x-4)2+3
y=100-5x2
y=-3(x-4)(x+5)自变量x的取值范围是什么?它的图像是什么?抛物线任何实数下列函数中,哪些是二次函数?做一做:是不是是是不是 知识点: 二次函数y=ax2、y=a(x+m)2
y=a(x+m)2+k的平移规律m决定左右平移,k 决定上下平移Y=-2(x-4)2+5是由哪条抛物线经怎样
平移得到的?Y=3x2-12x-4是由哪条抛物线经怎样
平移得到的?
二次函数的解析式有几种类型?练习:分别根据下列条件求二次函数的解析式:一般式:Y=ax2+bx+c
顶点式:y=a(x+m)2+k
交点式:y=a(x-x1)(x-x2)1、已知抛物线经过A(0,0),B(1,-3),C(2,-8)2、抛物线的顶点坐标为(-1,6),且过点(3,-2)3、已知抛物线与x轴的两个交点的横坐标为2,
-8,与y轴交于(0,4) 的图象是___,顶点坐标
是___,对称轴是___,当a﹥0时,抛物
线的开口向__,顶点是抛物线的最__,
当x__时,y随x的增大而减小,当x___
时,y随x的增大而增大;当x=__时,
y最小值=____.
当a﹤0时,开口向__,顶点是___,是抛
物线的最__.当x≤__时,y随x的增大而
___,当x≥__时,y随x的增大而___,当
X=__时,y最大值=____.y=ax2y=a(x+m)2
y=a(x+m)2+ky=ax2+bx+c知识点:
抛物线y=ax2+bx+c 与x轴的交点由_______决定.b2-4ac练习:判断下列抛物线与x轴的交点情况.1、y=2x2-4x+1
2、y=-3x2-4x-2
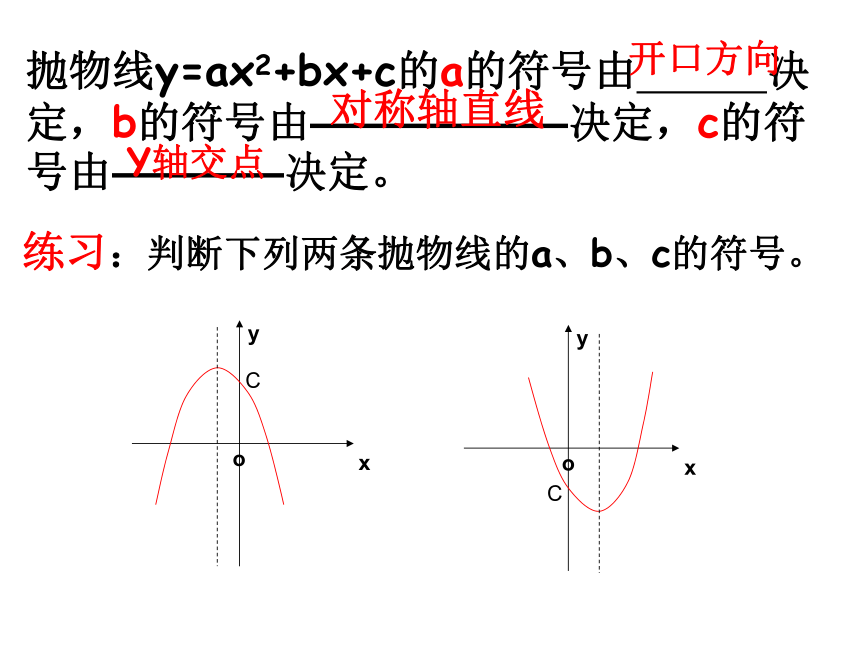
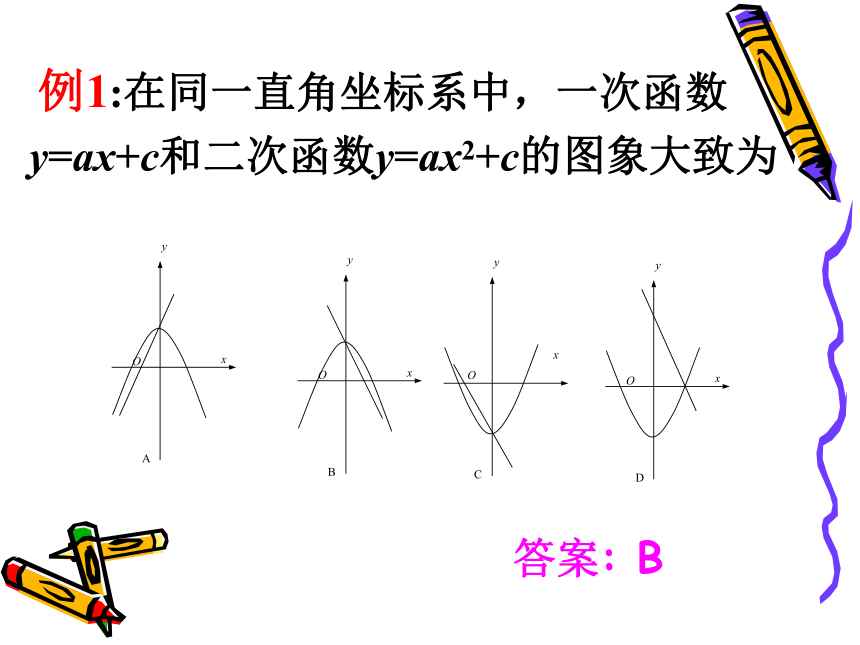
3、y=5x2+20x+20抛物线y=ax2+bx+c的a的符号由 决定,b的符号由——————决定,c的符号由————决定。练习:判断下列两条抛物线的a、b、c的符号。开口方向对称轴直线Y轴交点 例1:在同一直角坐标系中,一次函数y=ax+c和二次函数y=ax2+c的图象大致为答案: B五点法:顶点(- , )
与y轴交点(0,c),其关于抛
物线对称轴对称的对称点是
(- ,c),与x轴的两交点为
(x1,0),(x2,0)知识点:对称轴是直线x=-m 或x=- 或x=已知抛物线y=ax2+bx+c的图象过(3,5)与(-7,5)两点,求此抛物线的解析式三类二次函数解析式所得到的对称轴直线为:小练习:例2:填空:
(1)抛物线y=x2-3x+2与y轴的交点坐标是____________,与x轴的交点坐标是____________;
(2)抛物线y=-2x2+5x-3与y轴的交点坐标是____________,与x轴的交点坐标是____________. (0,2)(1,0)和(2,0)(0,-3)(1,0)和( 3/2 ,0)例3:已知抛物线y=x2-2x-8, (1)求证:该抛物线与x轴一定有两个交点; (2)若该抛物线与x轴的两个交点分别为A、B,且它的顶点为P,求△ABP的面积。试一试:
1、如图直线l经过点A(4,0)和B(0,4)两点,它与二次函数y=ax2的图像在第一象限内相交于P点,若△AOP的面积为4.5,求二次函数的解析式.2、已知二次函数y=2x2+8mx+2m+3,如果它的图像的顶点在x轴上,求m的值和顶点坐标.3、已知抛物线y=0.25x2,把它的顶点移到x轴上的点A, 所得的抛物线与y轴交于点B,且线段OA,OB满足关系OA-1 =OB,试说明平移方法.试一试:例4、在体育测试时,初三的一名高个子男
同学推铅球. 已知铅球所经过的路线是某个二次函数图像的一部分,如图所示,如果这个男同学的出手处A点的坐标(0,2),铅球路线的最高处B点的坐标为(6,5) (1)求这个二次函数的解析式; (2)该男同学把铅球推出去多远?(精确到0.01米 ) .yox24862461012B(6,5)A(0,2)C1、如图,两条钢缆具有相同的抛物线形状.按照图中的直角坐标系,左面的一条抛物线可以用y=0.0225x2+0.9x+10表示,而且左右两条抛物线关于y轴对称. ⑴钢缆的最低点到桥面的距离是
⑵两条钢缆最低点之间的距离是
(3)右边的抛物线解析式是1米40米2、已知某绿色蔬菜生产基地收获大蒜,从十月一日起开始上市的30天内,大蒜每千克的批发价y(元)是上市时间x(天)的二次函数,由近几年的行情可知如下信息:(1)求y关于x的函数关系式。(2)当大蒜每千克的批发价为10.8元 时,问是在上市的多少天?3、 已知二次函数y=3x2-6x+5,若它的顶点不动,把开口反向再沿对称轴平移,得到一条新抛物线,它恰好与y=mx-2交于点(2,-4),则新抛物线的解析式是什么?这节课你有什么收获和体会?
形如y=ax2+bx+c (a、b、c是常数,a≠0)的函数叫做x的二次函数 。二次函数的定义
说出下列二次函数的各项系数:
y=-x2
y=2(x-4)2+3
y=100-5x2
y=-3(x-4)(x+5)自变量x的取值范围是什么?它的图像是什么?抛物线任何实数下列函数中,哪些是二次函数?做一做:是不是是是不是 知识点: 二次函数y=ax2、y=a(x+m)2
y=a(x+m)2+k的平移规律m决定左右平移,k 决定上下平移Y=-2(x-4)2+5是由哪条抛物线经怎样
平移得到的?Y=3x2-12x-4是由哪条抛物线经怎样
平移得到的?
二次函数的解析式有几种类型?练习:分别根据下列条件求二次函数的解析式:一般式:Y=ax2+bx+c
顶点式:y=a(x+m)2+k
交点式:y=a(x-x1)(x-x2)1、已知抛物线经过A(0,0),B(1,-3),C(2,-8)2、抛物线的顶点坐标为(-1,6),且过点(3,-2)3、已知抛物线与x轴的两个交点的横坐标为2,
-8,与y轴交于(0,4) 的图象是___,顶点坐标
是___,对称轴是___,当a﹥0时,抛物
线的开口向__,顶点是抛物线的最__,
当x__时,y随x的增大而减小,当x___
时,y随x的增大而增大;当x=__时,
y最小值=____.
当a﹤0时,开口向__,顶点是___,是抛
物线的最__.当x≤__时,y随x的增大而
___,当x≥__时,y随x的增大而___,当
X=__时,y最大值=____.y=ax2y=a(x+m)2
y=a(x+m)2+ky=ax2+bx+c知识点:
抛物线y=ax2+bx+c 与x轴的交点由_______决定.b2-4ac练习:判断下列抛物线与x轴的交点情况.1、y=2x2-4x+1
2、y=-3x2-4x-2
3、y=5x2+20x+20抛物线y=ax2+bx+c的a的符号由 决定,b的符号由——————决定,c的符号由————决定。练习:判断下列两条抛物线的a、b、c的符号。开口方向对称轴直线Y轴交点 例1:在同一直角坐标系中,一次函数y=ax+c和二次函数y=ax2+c的图象大致为答案: B五点法:顶点(- , )
与y轴交点(0,c),其关于抛
物线对称轴对称的对称点是
(- ,c),与x轴的两交点为
(x1,0),(x2,0)知识点:对称轴是直线x=-m 或x=- 或x=已知抛物线y=ax2+bx+c的图象过(3,5)与(-7,5)两点,求此抛物线的解析式三类二次函数解析式所得到的对称轴直线为:小练习:例2:填空:
(1)抛物线y=x2-3x+2与y轴的交点坐标是____________,与x轴的交点坐标是____________;
(2)抛物线y=-2x2+5x-3与y轴的交点坐标是____________,与x轴的交点坐标是____________. (0,2)(1,0)和(2,0)(0,-3)(1,0)和( 3/2 ,0)例3:已知抛物线y=x2-2x-8, (1)求证:该抛物线与x轴一定有两个交点; (2)若该抛物线与x轴的两个交点分别为A、B,且它的顶点为P,求△ABP的面积。试一试:
1、如图直线l经过点A(4,0)和B(0,4)两点,它与二次函数y=ax2的图像在第一象限内相交于P点,若△AOP的面积为4.5,求二次函数的解析式.2、已知二次函数y=2x2+8mx+2m+3,如果它的图像的顶点在x轴上,求m的值和顶点坐标.3、已知抛物线y=0.25x2,把它的顶点移到x轴上的点A, 所得的抛物线与y轴交于点B,且线段OA,OB满足关系OA-1 =OB,试说明平移方法.试一试:例4、在体育测试时,初三的一名高个子男
同学推铅球. 已知铅球所经过的路线是某个二次函数图像的一部分,如图所示,如果这个男同学的出手处A点的坐标(0,2),铅球路线的最高处B点的坐标为(6,5) (1)求这个二次函数的解析式; (2)该男同学把铅球推出去多远?(精确到0.01米 ) .yox24862461012B(6,5)A(0,2)C1、如图,两条钢缆具有相同的抛物线形状.按照图中的直角坐标系,左面的一条抛物线可以用y=0.0225x2+0.9x+10表示,而且左右两条抛物线关于y轴对称. ⑴钢缆的最低点到桥面的距离是
⑵两条钢缆最低点之间的距离是
(3)右边的抛物线解析式是1米40米2、已知某绿色蔬菜生产基地收获大蒜,从十月一日起开始上市的30天内,大蒜每千克的批发价y(元)是上市时间x(天)的二次函数,由近几年的行情可知如下信息:(1)求y关于x的函数关系式。(2)当大蒜每千克的批发价为10.8元 时,问是在上市的多少天?3、 已知二次函数y=3x2-6x+5,若它的顶点不动,把开口反向再沿对称轴平移,得到一条新抛物线,它恰好与y=mx-2交于点(2,-4),则新抛物线的解析式是什么?这节课你有什么收获和体会?
同课章节目录
