二次函数复习[上学期]
图片预览

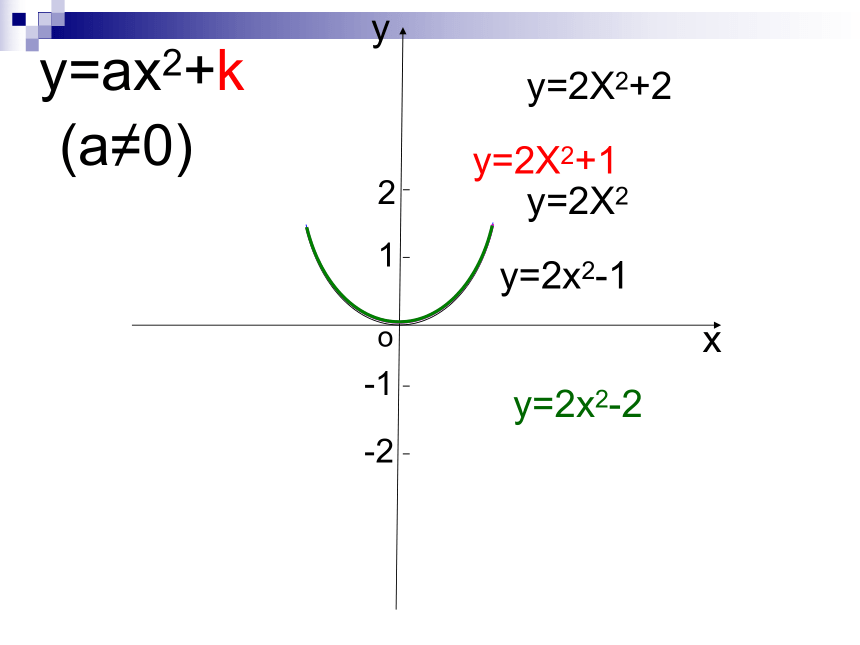




文档简介
课件21张PPT。说一说:通过二次函数的学习,
你应该学什么?你学会了什么?1 理解二次函数的概念;2 会用描点法画出二次函数的图象;会用配方法和公式确定抛物线的开口方向,
对称轴,顶点坐标;4 会用待定系数法求二次函数的解析式; 5 能用二次函数的知识解决生活中的实际问题
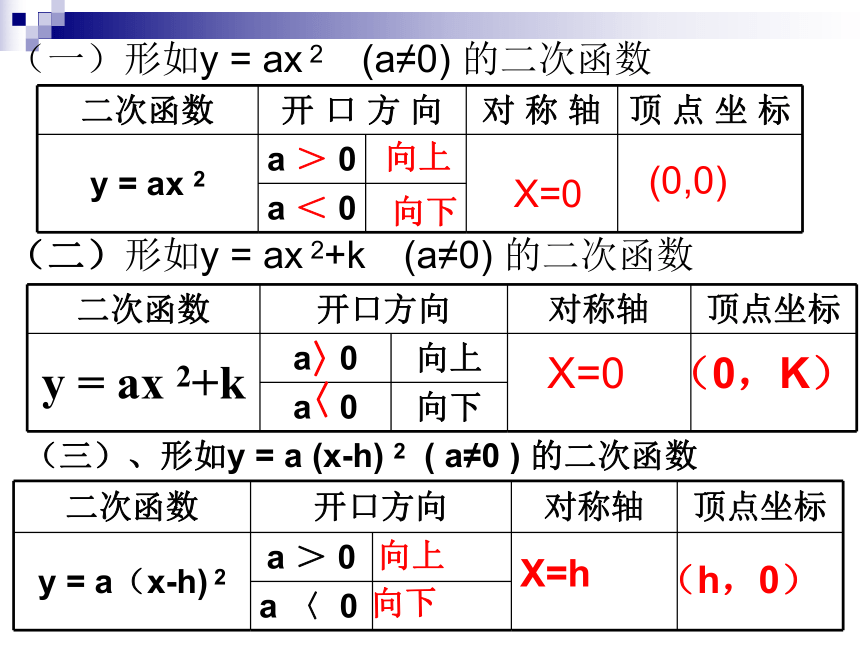
及简单的综合运用。二次函数复习(一)形如y = ax 2 (a≠0) 的二次函数 向上向下X=0(0,0)(二)形如y = ax 2+k (a≠0) 的二次函数〉〈X=0(0,K)向上向下X=h(h,0)(三)、形如y = a (x-h) 2 ( a≠0 ) 的二次函数y=2X2y=2X2+1y=2X2+2y=2x2-1y=2x2-2y=ax2+k(a≠0)巩固练习1:
(1)抛物线y = x 2的开口向 ,对称轴是 ,顶点坐标是 ,图象过第 象限 ;(2)已知y = - nx 2 (n>0) , 则图象 ( )
(填“可能”或“不可能”)过点A(-2,3)。上Y轴(0,0)一、二不可能上X=0(0,3)上3(2)已知(如图)抛物线y = ax 2+k的图象,则a 0,k 0;若图象过A (0,-2) 和B (2,0) ,则a = ,k = ;函数关系式是y = 。〉〈0.5-20.5x 2-2(四) 形如y = a (x-h) 2 +k (a ≠0) 的二次函数a > 0 a < 0X=h(h,k)练习巩固2:
(1)抛物线 y = 2 (x -1/2 ) 2+1 的开口向 , 对称轴 , 顶点坐标是
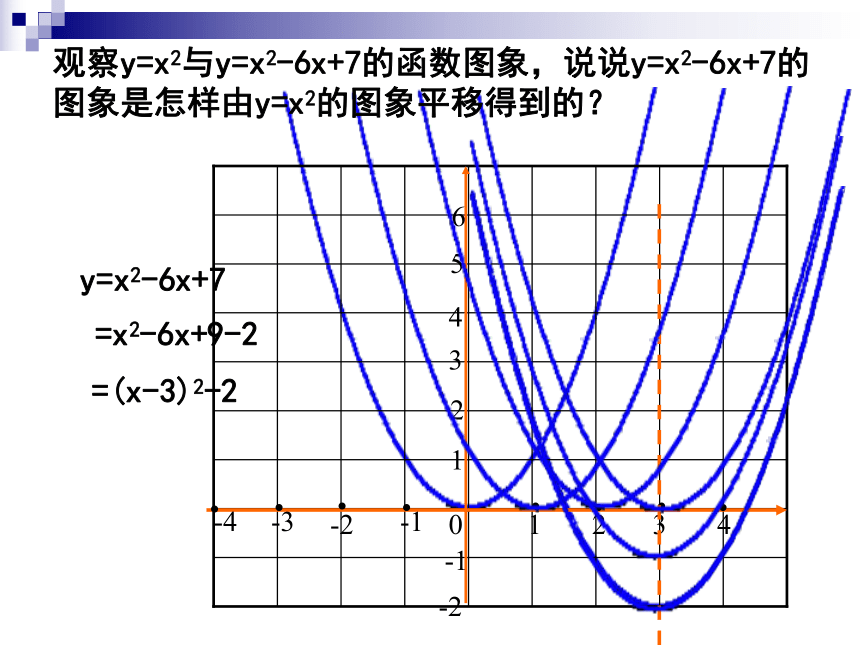
(2)若抛物线y = a (x+m) 2+n开口向下,顶点在第四象限,则a 0, m 0, n 0。 上X=1/2(1/2,1)〈〈〈0观察y=x2与y=x2-6x+7的函数图象,说说y=x2-6x+7的图象是怎样由y=x2的图象平移得到的?y=x2-6x+7=x2-6x+9-2=(x-3)2-2基础练习 1.由y=2x2的图象向左平移两个单位,再向下平
移三个单位,得到的图象的函数解析式为
________________________2.由函数y= -3(x-1)2+2的图象向右平移4个单位,
再向上平移3个单位,得到的图象的函数解析式
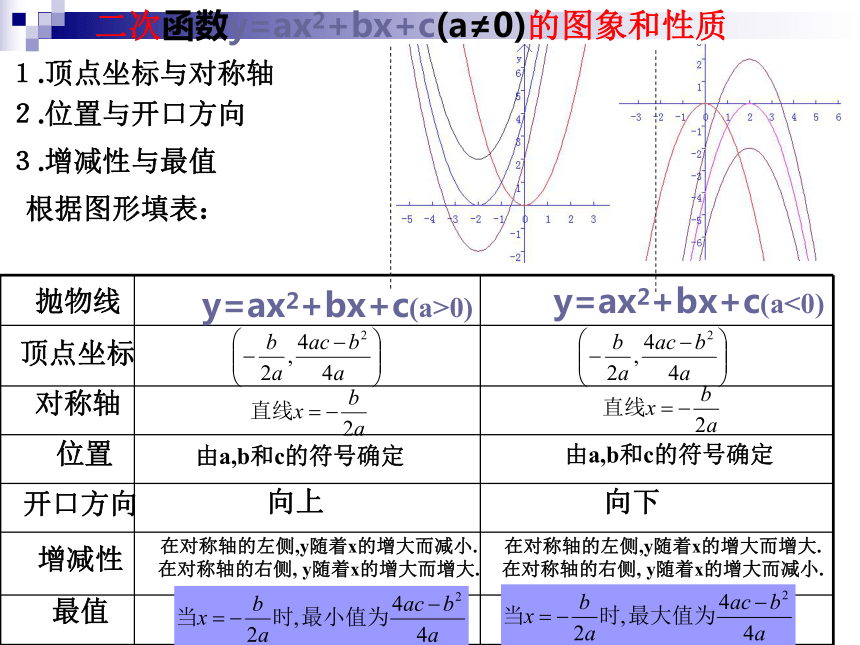
为_____________________________y=2(x+2)2-3=2x2+8x+5y= - 3(x-1-4)2+2+3=-3x2+30x-703.抛物线y=ax2向左平移一个单位,再向下平移8个单位且y=ax2过点(1,2).则平移后的解析式为______________;y=2(x+1)2-84.将抛物线y=x2-6x+4如何移动才能得到y=x2.逆向思考,由y=x2-6x+4 =(x-3)2-5知:先向左平移3个单位,再向上平移5个单位.二次函数y=ax2+bx+c(a≠0)的图象和性质1.顶点坐标与对称轴2.位置与开口方向3.增减性与最值抛物线顶点坐标对称轴位置开口方向增减性最值y=ax2+bx+c(a>0)y=ax2+bx+c(a<0)由a,b和c的符号确定由a,b和c的符号确定向上向下在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大. 在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小. 根据图形填表:a决定了抛物线的____和___
对称轴由___决定;
c决定了图象与_____轴的交点位置;开口方向形状a和by当a的绝对值相等时,其形状完全相同,当a的绝对值越大,则开口越小,反之成立1.已知y=ax2+bx+c的图象如图所示,
a___0, b____0, c_____0, abc____0
b___2a, 2a-b_____0, 2a+b_______0
b2-4ac_____0
a+b+c_____0, a-b+c____0
4a-2b+c_____0二次函数与一元二次方程二次函数y=ax2+bx+c的图象和x轴交点有三种情况:有两个交点,有一个交点,没有交点.当二次函数y=ax2+bx+c的图象和x轴有交点时,交点的横坐标就是当y=0时自变量x的值,即一元二次方程ax2+bx+c=0的根.有两个交点有两个相异的实数根b2-4ac > 0有一个交点有两个相等的实数根b2-4ac = 0没有交点没有实数根b2-4ac < 0若两交点坐标分别为( x1,0)、 (x2,0)
则x1 +x2=__, x1 x2=__,
两交点的距离为|x1 -x2 |=2.选择
抛物线y=x2-4x+3的对称轴是_____________.
A 直线x=1 B直线x= -1 C 直线x=2 D直线x= -2
(2)抛物线y=3x2-1的________________
A 开口向上,有最高点 B 开口向上,有最低点
C 开口向下,有最高点 D 开口向下,有最低点
(3)若y=ax2+bx+c(a ? 0)与轴交于点A(2,0), B(4,0),
则对称轴是_______
A 直线x=2 B直线x=4 C 直线x=3 D直线x= -3
(4)若y=ax2+bx+c(a ? 0)与轴交于点A(2,m), B(4,m),
则对称轴是_______
A 直线x=3 B 直线x=4 C 直线x= -3 D直线x=2
cBCAABAB 对称是一种数学美,它展示出
整体的和谐与平衡之美,抛物线是
轴对称图形,解题中应积极捕捉,
创造对称关系,以便从整体上把握
问题,由抛物线捕捉对称信息的方
式有:1.从抛物线上两点的纵坐标
相等获得对称信息;2.从抛物线上两点之间的线段被抛物线的对称轴垂直平分获得对称信息.2、已知抛物线顶点坐标(h, k),通常设抛物线解析式为_______________3、已知抛物线与x 轴的两个交点(x1,0)、 (x2,0),通常设解析式为_____________1、已知抛物线上的三点,通常设解析式为________________y=ax2+bx+c(a≠0)y=a(x-h)2+k(a≠0)y=a(x-x1)(x-x2) (a≠0)求抛物线解析式的三种方法练习 根据下列条件,求二次函数的解析式。(1)、图象经过(0,0), (1,-2) , (2,3) 三点;(2)、图象的顶点(2,3), 且经过点(3,1) ;(3)、图象经过(0,0), (12,0) ,且最高点
的纵坐标是3 。 例1、已知二次函数y=ax2+bx+c的最大值是2,图象顶点在直线y=x+1上,并且图象经过点(3,-6)。求a、b、c。解:∵二次函数的最大值是2
∴抛物线的顶点纵坐标为2
又∵抛物线的顶点在直线y=x+1上
∴当y=2时,x=1 ∴顶点坐标为( 1 , 2)
∴设二次函数的解析式为y=a(x-1)2+2
又∵图象经过点(3,-6)
∴-6=a (3-1)2+2 ∴a=-2
∴二次函数的解析式为y=-2(x-1)2+2
即: y=-2x2+4x综合创新:
1.已知抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的
形状相同,顶点在直线x=1上,且顶点到x轴的距离
为5,请写出满足此条件的抛物线的解析式.解:?抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的形状
相同? a=1或-1
又?顶点在直线x=1上,且顶点到x轴的距离为5,
? 顶点为(1,5)或(1,-5)
所以其解析式为:
(1) y=(x-1)2+5 (2) y=(x-1)2-5
(3) y=-(x-1)2+5 (4) y=-(x-1)2-5
展开成一般式即可.
2.若a+b+c=0,a?0,把抛物线y=ax2+bx+c向下
平移4个单位,再向左平移5个单位所到的新
抛物线的顶点是(-2,0),求原抛物线的解析式.分析:(1)由a+b+c=0可知,原抛物线的图象经过(1,0)(2) 新抛物线向右平移5个单位,
再向上平移4个单位即得原抛物线答案:y=-x2+6x-5练习1、已知抛物线y=ax2+bx-1的对称轴是x=1 ,
最高点在直线y=2x+4上。
(1)求抛物线解析式.(2)求抛物线与直线的交点坐标.解:∵二次函数的对称轴是x=1
∴图象的顶点横坐标为1
又∵图象的最高点在直线y=2x+4上
∴当x=1时,y=6
∴顶点坐标为( 1 , 6)
例2、已知抛物线y=ax2+bx+c与x轴正、负半轴分别交于A、B两点,与y轴负半轴交于点C。若OA=4,OB=1,∠ACB=90°,求抛物线解析式。解: ∵点A在正半轴,点B在负半轴
OA=4,∴点A(4,0)
OB=1, ∴点B(-1,0)
又 ∵ ∠ACB=90°
∴OC2=OA·OB=4
∴OC=2,点C(0,-2)练习、已知二次函数y=ax2-5x+c的图象如图。(1)、当x为何值时,y随x的增大而增大;
(2)、当x为何值时,y<0。(3)、求它的解析式和顶点坐标; 问题2这位同学身高1.7 m,若在这次跳投中,球在头顶上方0.25 m处出手,问:球出手时,他跳离地面的高度是多少?尝试成功 如图,有一次,我班某同学在距篮下4m处跳起投篮,球运行的路线是抛物线,当球运行的水平距离2.5m时,达到最大高度3.5m,然后准确落入篮圈。已知篮圈中心到地面的距离为3.05m. 3.05 m2.5m3.5m问题1 建立如图所示的直角坐标系,求抛物线的解析式;4 m试一试 你知道吗?平时我们在跳绳时,绳甩到最高处的形状可近似的看为抛物线,如图所示,正在甩绳的甲、乙两名学生拿绳的手间距为4米,距地面均为1米,学生丙、丁分别站在距甲拿绳的手水平距离1米、2.5米处,绳子甩到最高处时,刚好通过他们的头顶,已知学生丙的身高是1.5米,请你算一算学生丁的身高。1m2.5m4m1m甲乙丙丁(0,1)(4,1)(1,1.5)练习:在矩形荒地ABCD中,AB=a,BC=b,(a>b > 0),今在四边上分别选取E、F、G、H四点,且AE=AH=CF=CG=x,建一个花园,如何设计,可使花园面积最大?DCABGHFEabb
你应该学什么?你学会了什么?1 理解二次函数的概念;2 会用描点法画出二次函数的图象;会用配方法和公式确定抛物线的开口方向,
对称轴,顶点坐标;4 会用待定系数法求二次函数的解析式; 5 能用二次函数的知识解决生活中的实际问题
及简单的综合运用。二次函数复习(一)形如y = ax 2 (a≠0) 的二次函数 向上向下X=0(0,0)(二)形如y = ax 2+k (a≠0) 的二次函数〉〈X=0(0,K)向上向下X=h(h,0)(三)、形如y = a (x-h) 2 ( a≠0 ) 的二次函数y=2X2y=2X2+1y=2X2+2y=2x2-1y=2x2-2y=ax2+k(a≠0)巩固练习1:
(1)抛物线y = x 2的开口向 ,对称轴是 ,顶点坐标是 ,图象过第 象限 ;(2)已知y = - nx 2 (n>0) , 则图象 ( )
(填“可能”或“不可能”)过点A(-2,3)。上Y轴(0,0)一、二不可能上X=0(0,3)上3(2)已知(如图)抛物线y = ax 2+k的图象,则a 0,k 0;若图象过A (0,-2) 和B (2,0) ,则a = ,k = ;函数关系式是y = 。〉〈0.5-20.5x 2-2(四) 形如y = a (x-h) 2 +k (a ≠0) 的二次函数a > 0 a < 0X=h(h,k)练习巩固2:
(1)抛物线 y = 2 (x -1/2 ) 2+1 的开口向 , 对称轴 , 顶点坐标是
(2)若抛物线y = a (x+m) 2+n开口向下,顶点在第四象限,则a 0, m 0, n 0。 上X=1/2(1/2,1)〈〈〈0观察y=x2与y=x2-6x+7的函数图象,说说y=x2-6x+7的图象是怎样由y=x2的图象平移得到的?y=x2-6x+7=x2-6x+9-2=(x-3)2-2基础练习 1.由y=2x2的图象向左平移两个单位,再向下平
移三个单位,得到的图象的函数解析式为
________________________2.由函数y= -3(x-1)2+2的图象向右平移4个单位,
再向上平移3个单位,得到的图象的函数解析式
为_____________________________y=2(x+2)2-3=2x2+8x+5y= - 3(x-1-4)2+2+3=-3x2+30x-703.抛物线y=ax2向左平移一个单位,再向下平移8个单位且y=ax2过点(1,2).则平移后的解析式为______________;y=2(x+1)2-84.将抛物线y=x2-6x+4如何移动才能得到y=x2.逆向思考,由y=x2-6x+4 =(x-3)2-5知:先向左平移3个单位,再向上平移5个单位.二次函数y=ax2+bx+c(a≠0)的图象和性质1.顶点坐标与对称轴2.位置与开口方向3.增减性与最值抛物线顶点坐标对称轴位置开口方向增减性最值y=ax2+bx+c(a>0)y=ax2+bx+c(a<0)由a,b和c的符号确定由a,b和c的符号确定向上向下在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大. 在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小. 根据图形填表:a决定了抛物线的____和___
对称轴由___决定;
c决定了图象与_____轴的交点位置;开口方向形状a和by当a的绝对值相等时,其形状完全相同,当a的绝对值越大,则开口越小,反之成立1.已知y=ax2+bx+c的图象如图所示,
a___0, b____0, c_____0, abc____0
b___2a, 2a-b_____0, 2a+b_______0
b2-4ac_____0
a+b+c_____0, a-b+c____0
4a-2b+c_____0二次函数与一元二次方程二次函数y=ax2+bx+c的图象和x轴交点有三种情况:有两个交点,有一个交点,没有交点.当二次函数y=ax2+bx+c的图象和x轴有交点时,交点的横坐标就是当y=0时自变量x的值,即一元二次方程ax2+bx+c=0的根.有两个交点有两个相异的实数根b2-4ac > 0有一个交点有两个相等的实数根b2-4ac = 0没有交点没有实数根b2-4ac < 0若两交点坐标分别为( x1,0)、 (x2,0)
则x1 +x2=__, x1 x2=__,
两交点的距离为|x1 -x2 |=2.选择
抛物线y=x2-4x+3的对称轴是_____________.
A 直线x=1 B直线x= -1 C 直线x=2 D直线x= -2
(2)抛物线y=3x2-1的________________
A 开口向上,有最高点 B 开口向上,有最低点
C 开口向下,有最高点 D 开口向下,有最低点
(3)若y=ax2+bx+c(a ? 0)与轴交于点A(2,0), B(4,0),
则对称轴是_______
A 直线x=2 B直线x=4 C 直线x=3 D直线x= -3
(4)若y=ax2+bx+c(a ? 0)与轴交于点A(2,m), B(4,m),
则对称轴是_______
A 直线x=3 B 直线x=4 C 直线x= -3 D直线x=2
cBCAABAB 对称是一种数学美,它展示出
整体的和谐与平衡之美,抛物线是
轴对称图形,解题中应积极捕捉,
创造对称关系,以便从整体上把握
问题,由抛物线捕捉对称信息的方
式有:1.从抛物线上两点的纵坐标
相等获得对称信息;2.从抛物线上两点之间的线段被抛物线的对称轴垂直平分获得对称信息.2、已知抛物线顶点坐标(h, k),通常设抛物线解析式为_______________3、已知抛物线与x 轴的两个交点(x1,0)、 (x2,0),通常设解析式为_____________1、已知抛物线上的三点,通常设解析式为________________y=ax2+bx+c(a≠0)y=a(x-h)2+k(a≠0)y=a(x-x1)(x-x2) (a≠0)求抛物线解析式的三种方法练习 根据下列条件,求二次函数的解析式。(1)、图象经过(0,0), (1,-2) , (2,3) 三点;(2)、图象的顶点(2,3), 且经过点(3,1) ;(3)、图象经过(0,0), (12,0) ,且最高点
的纵坐标是3 。 例1、已知二次函数y=ax2+bx+c的最大值是2,图象顶点在直线y=x+1上,并且图象经过点(3,-6)。求a、b、c。解:∵二次函数的最大值是2
∴抛物线的顶点纵坐标为2
又∵抛物线的顶点在直线y=x+1上
∴当y=2时,x=1 ∴顶点坐标为( 1 , 2)
∴设二次函数的解析式为y=a(x-1)2+2
又∵图象经过点(3,-6)
∴-6=a (3-1)2+2 ∴a=-2
∴二次函数的解析式为y=-2(x-1)2+2
即: y=-2x2+4x综合创新:
1.已知抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的
形状相同,顶点在直线x=1上,且顶点到x轴的距离
为5,请写出满足此条件的抛物线的解析式.解:?抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的形状
相同? a=1或-1
又?顶点在直线x=1上,且顶点到x轴的距离为5,
? 顶点为(1,5)或(1,-5)
所以其解析式为:
(1) y=(x-1)2+5 (2) y=(x-1)2-5
(3) y=-(x-1)2+5 (4) y=-(x-1)2-5
展开成一般式即可.
2.若a+b+c=0,a?0,把抛物线y=ax2+bx+c向下
平移4个单位,再向左平移5个单位所到的新
抛物线的顶点是(-2,0),求原抛物线的解析式.分析:(1)由a+b+c=0可知,原抛物线的图象经过(1,0)(2) 新抛物线向右平移5个单位,
再向上平移4个单位即得原抛物线答案:y=-x2+6x-5练习1、已知抛物线y=ax2+bx-1的对称轴是x=1 ,
最高点在直线y=2x+4上。
(1)求抛物线解析式.(2)求抛物线与直线的交点坐标.解:∵二次函数的对称轴是x=1
∴图象的顶点横坐标为1
又∵图象的最高点在直线y=2x+4上
∴当x=1时,y=6
∴顶点坐标为( 1 , 6)
例2、已知抛物线y=ax2+bx+c与x轴正、负半轴分别交于A、B两点,与y轴负半轴交于点C。若OA=4,OB=1,∠ACB=90°,求抛物线解析式。解: ∵点A在正半轴,点B在负半轴
OA=4,∴点A(4,0)
OB=1, ∴点B(-1,0)
又 ∵ ∠ACB=90°
∴OC2=OA·OB=4
∴OC=2,点C(0,-2)练习、已知二次函数y=ax2-5x+c的图象如图。(1)、当x为何值时,y随x的增大而增大;
(2)、当x为何值时,y<0。(3)、求它的解析式和顶点坐标; 问题2这位同学身高1.7 m,若在这次跳投中,球在头顶上方0.25 m处出手,问:球出手时,他跳离地面的高度是多少?尝试成功 如图,有一次,我班某同学在距篮下4m处跳起投篮,球运行的路线是抛物线,当球运行的水平距离2.5m时,达到最大高度3.5m,然后准确落入篮圈。已知篮圈中心到地面的距离为3.05m. 3.05 m2.5m3.5m问题1 建立如图所示的直角坐标系,求抛物线的解析式;4 m试一试 你知道吗?平时我们在跳绳时,绳甩到最高处的形状可近似的看为抛物线,如图所示,正在甩绳的甲、乙两名学生拿绳的手间距为4米,距地面均为1米,学生丙、丁分别站在距甲拿绳的手水平距离1米、2.5米处,绳子甩到最高处时,刚好通过他们的头顶,已知学生丙的身高是1.5米,请你算一算学生丁的身高。1m2.5m4m1m甲乙丙丁(0,1)(4,1)(1,1.5)练习:在矩形荒地ABCD中,AB=a,BC=b,(a>b > 0),今在四边上分别选取E、F、G、H四点,且AE=AH=CF=CG=x,建一个花园,如何设计,可使花园面积最大?DCABGHFEabb
同课章节目录
