二次函数复习[上学期]

课件22张PPT。二次函数复习课（2）小练习:(2004浙江)关于二次函数y=(x+2)2-3的最大(小)值,叙述正确的是( )A.当x=2是,有最大值-3; B.当x=-2时,有最大值-3;
C.当x=2是,有最小值-3; D.当x=-2时,有最小值-3.要点:二次函数y=a(x-h)2+k,当a>0时,开口向上,图象有最低点,函数有最小值.当x=h时,函数有最小值k;当a<0时,开口向下,图象有最高点,函数有最大值.当x=h时,函数有最大值k.D( 1 )图象过A(0，1) 、B（1，2）、C（2，-1）三点 (1) 已知抛物线y=ax2+bx+c满足下列条件,求函数的解析式.（1）解：设抛物线的解析式为y=ax2+bx+c∵图象过A(0，1) 、B（1，2）、C（2，-1）三点
∴∴∴y= -2x2+3x+1解：∵A(1，0)，对称轴为x=2∴抛物线与x轴另一个交点C应为（3，0）∴设其解析式为y=a(x-1)(x-3)
∵B（0，-3）∴-3=a（0-1）（0-3）∴a= -1∴y= -(x-1)(x-3)
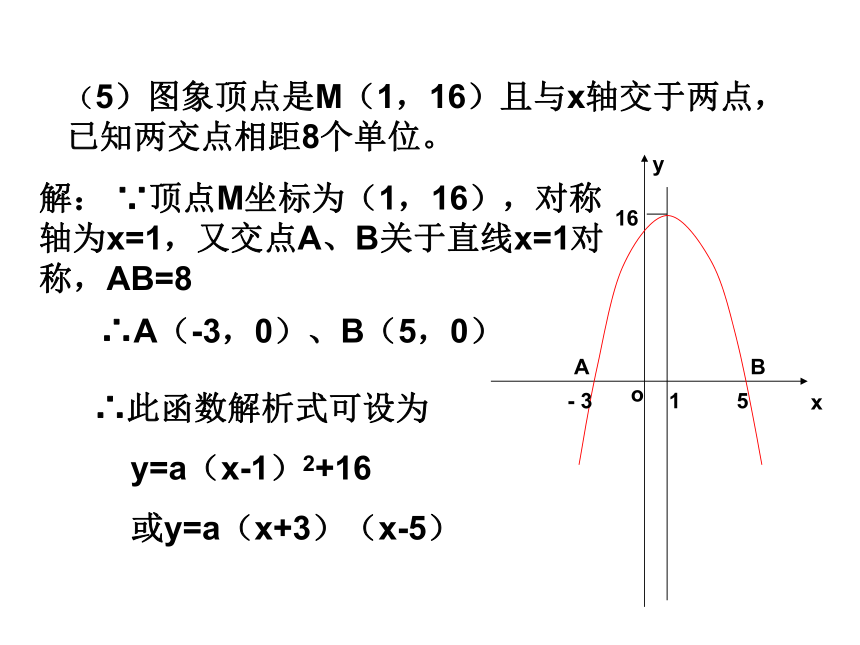
（2）图象经过A（1，0）、B（0，-3），且对称轴是直线x=21AB-3C3（3）图象顶点是（-2，3），且经过点（-1，5）解：∵图象顶点是（-2，3）∴设其解析式为y=a（x+2）2+3∵图象经过点（-1，5）∴5=a（-1+2）2+3∴a=2∴y=2（x+2）2+3（4）图象和x轴交于（-2，0）、（4，0）两点且顶点为（1，-4.5）解：由于题中告诉了图象与x轴的交点坐标，又告诉了顶点坐标，所以既可以用两根式又可以用顶点式来设其解析式设解析式为：y=a(x+2)(x-4)∴-4.5=a(1+2)(1-4)∵顶点为（1，-4.5） ∴a= -0.5∴y= -1/2(x+2)(x-4)（5）图象顶点是M（1，16）且与x轴交于两点，已知两交点相距8个单位。解： ∵顶点M坐标为（1，16），对称轴为x=1，又交点A、B关于直线x=1对称，AB=8∴A（-3，0）、B（5，0）∴此函数解析式可设为
y=a（x-1）2+16
或y=a（x+3）（x-5）116AB- 35例1、求满足下列条件的抛物线的解析式(1)经过点A（2，4），B（-1，0）且在x轴上截得的线段长为2解： ∵B（-1，0）且在x轴上截得的线段长为2∴抛物线与x轴的另一个交点坐标为C（-3，0）或C’（1，0）∴设抛物线的解析式为y=a（x- x1）（x- x2）①当抛物线经过B、C两点时，解析式为y=a（x+1）（x+3）又∵抛物线经过A（2，4）∴4=a（2+1）（2+3）②当抛物线经过B、C’ 两点时，解析式为y=a（x+1）（x-1）解法同(1)B-1- 31CC’∴a=∴y= （x+1）（x+3）
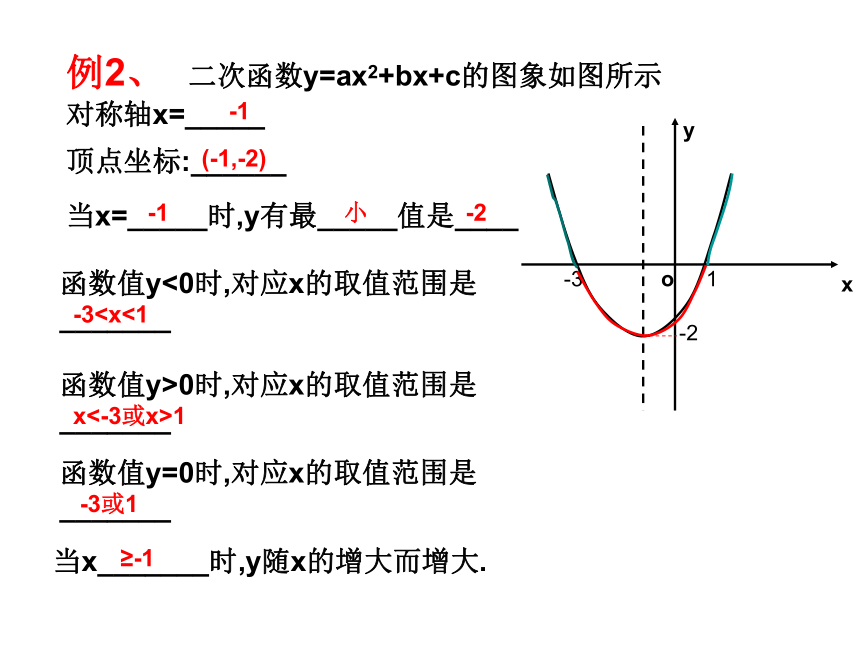
例2、 二次函数y=ax2+bx+c的图象如图所示对称轴x=_____顶点坐标:______当x=_____时,y有最_____值是____函数值y<0时,对应x的取值范围是_______函数值y>0时,对应x的取值范围是_______
函数值y=0时,对应x的取值范围是_______
当x_______时,y随x的增大而增大.-1(-1,-2)-1 小-2-31-3或1≥-1例3、已知二次函数
y=ax2+bx+c的图象如图所
示,下列结论①a+ b + c<0
②a – b + c>0 ③abc>0 ④
b=2a。其中正确的结论的
个数是（ ）
A 1个 B 2个 C 3个 D 4个mnD练一练：抛物线y=ax2+bx+c如图所示，试确定a、b、c、b2-4ac的符号：xyo练一练：抛物线y=ax2+bx+c如图所示，试确定a、b、c、 b2-4ac的符号：xyo练一练：已知：二次函数y=ax2+bx+c的图象如图所示，则点M（ ，a）在（ ）A、第一象限
B、第二象限
C、第三象限
D、第四象限 xoyD已知：一次函数y=ax+c与二次函数y=ax2+bx+c，它们在同一坐标系中的大致图象是图中的（ ）练一练：（A）（B）（C）（D）C试一试：
1、如图直线l经过点A(4,0)和B(0,4)两点,它与二次函数y=ax2的图像在第一象限内相交于P点,若△AOP的面积为4,求二次函数的解析式.2、 已知二次函数y=3x2-6x+5，若它的顶点不动，把开口反向再沿对称轴平移，得到一条新抛物线，它恰好过点（2，-4），则新抛物线的解析式是什么？
(3)当矩形的两边长为多少时,面积最大?是多少?试一试:
要用长20m的铁栏杆，一面靠墙，围成一个矩形的花圃，设连墙的一边为x,矩形的面积为y,求：(1)写出y关于x的函数式.
(2)当x=3时,矩形的面积为多少?(o ∴当x=5时，y的最大值为50。 例4、某商人如果将进货单价为8元的商品按每件10元出售，每天可销售100件，现在他采用提高出售价格，减少进货量的办法增加利润，已知这种商品每涨价一元，其销售量将减少10件，问他将出售价定为多少元时，才能使每天所获利润最大？并且求出最大利润是多少？解：设利润为y元，售价为x元，则每天可销售100-10(x-10)件，依题意得：

y=(x-8)([100-10(x-10)]
化简得
y= -10x2-280x -1600
配方得
y= -10(x-14)2 + 360

∴当 (x-14)2 =0时，即x=14时，y 有最大值是360

答：当定价为14元时，所获利润最大，最大利润是360元。 典型例题典型例题 例5:如图、等腰三角形的腰长和正方形的边长为4，等腰三角形以2米/秒的速度沿直线向正方形移动，直到AB与CD重合。设x秒时，三角形与正方形重叠部分的面积为y平方米.
(1)写出y与x的函数关系式及自变量的取值范围
(2)当重叠部分的面积是正方形的面积的一半时,三角形移动了多长时间?思考:如果继续向前移动,则重叠部分面积又会如何变化?O1.如图，二次函数y=x2-4x+3的图象交x轴于A、B 两点，交y轴于点C。则函数的对称轴方程是： ；顶点坐是 ；
与x轴的交点坐标是 ， ；与y轴的交点坐标是 ;函数的最小值是： ；△ABC的面积是 ；2、已知函数y=ax2+bx+c的图象如下图所示，则函数y=ax+b的图象只可能是（ ）
直线x=2(2,-1)(1,0)(0,3)-13(3,0)B再提高: 心理学家研究发现：一般情况下，学生的注意力随着教师讲课时间的变化而变化，讲课开始时，学生的注意力y随时间t的变化规律有如下关系式：（1）讲课开始后第5分钟时与讲课开始后第25分钟时比较，何时学生的注意力更集中？（2）讲课开始后多少分钟，学生的注意力最集中？能持续多少分钟？（3）一道数学难题，需要讲解24分钟，为了效果较好，要求学生的注意力最低达到180，那么经过适当安排，老师能否在学生注意力达到所需的状态下讲解完这道题目？中考题选练 已知二次函数 y=0.5x2+bx+c 的图象经过点A(0，-2)， 求证：这个二次函数图象的对称轴是直线 x＝3。
题目中的黑色部分是一段被墨水污染了无法辨认的文字。
（1）根据已知和结论中现有的信息，你能否求出题中的二次函数解析式？若能，请写出求解过程，并画出二次函数的图象。若不能，请说明理由。
（2）请你根据已有的信息，在原题中的黑色部分添加一个适当的条件，把原题补充完整。