二次函数复习[上学期]

课件14张PPT。二次函数-----复习课yx
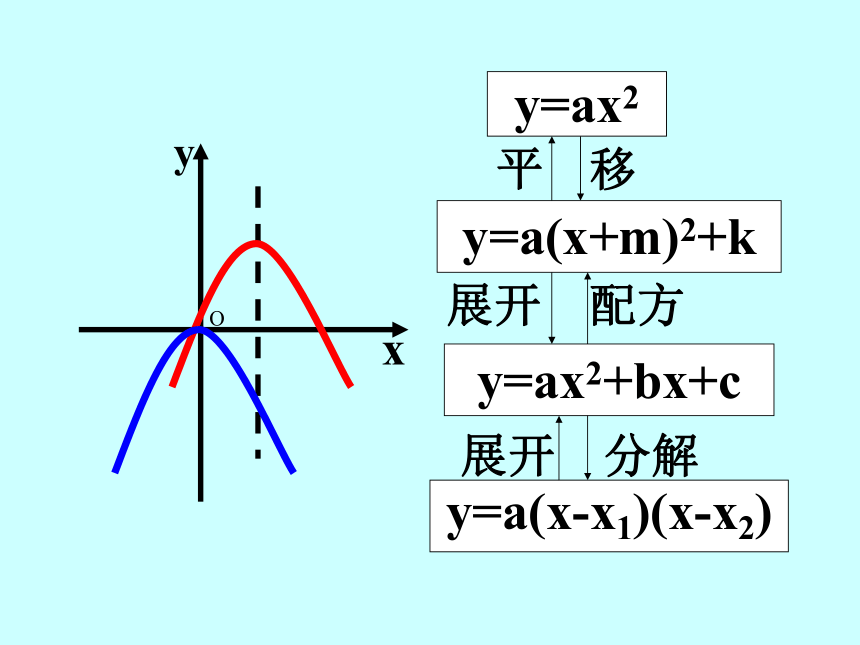
y=ax2y=a(x+m)2+ky=ax2+bx+cy=a(x-x1)(x-x2)平移展开　配方展开分解Oyx00yx0yx二次函数y= - x2+2x+3图像如图所示，
求 （1）最大值？对称轴?
（2）求A，B，C坐标?
（3）AB的长？
（4）求S△ABC？
（5）怎样平移一次，
使抛物线过原点？
　 （6）当x=1.88时，y=m;
x=1.99,y=n;则m___n.
（7）当x=0.88时， y=m;
x=1.99,y=n;则m___n.
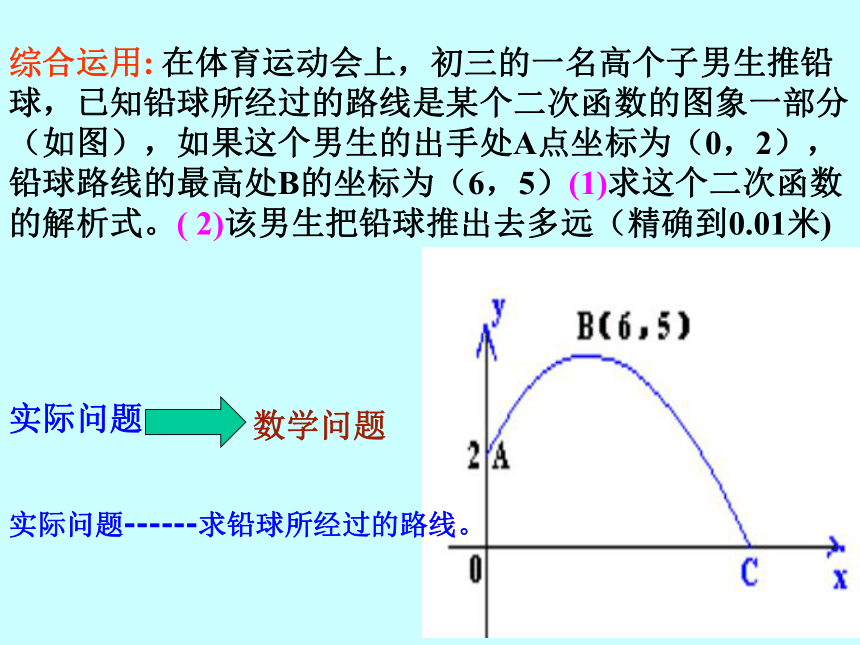
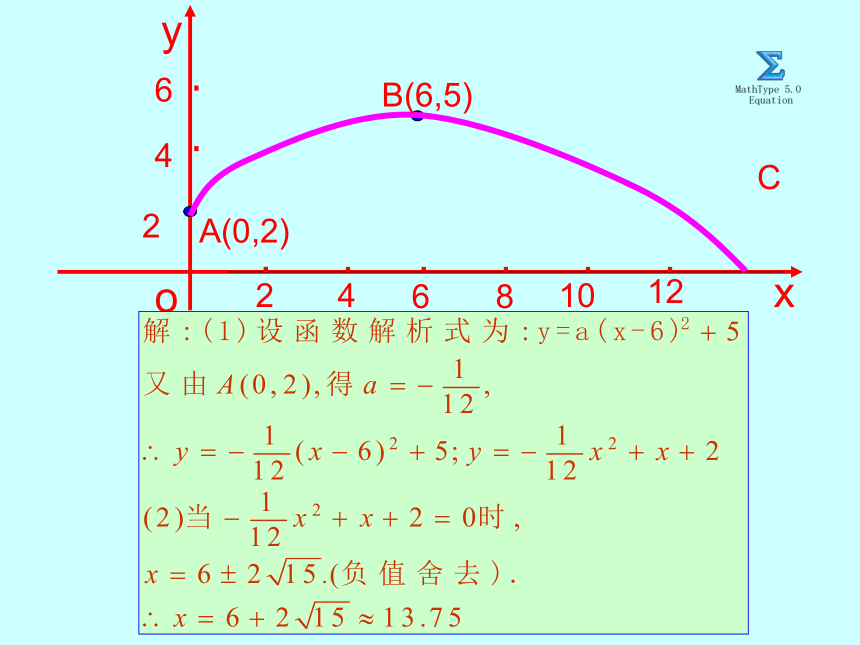
x0ABC y知识回顾:综合运用: 在体育运动会上，初三的一名高个子男生推铅球，已知铅球所经过的路线是某个二次函数的图象一部分（如图），如果这个男生的出手处A点坐标为（0，2），铅球路线的最高处B的坐标为（6，5）(1)求这个二次函数的解析式。( 2)该男生把铅球推出去多远（精确到0.01米)实际问题数学问题实际问题------求铅球所经过的路线。C 1。如图，一位运动员在距篮下4米处跳起投篮，球运行的路线是抛物线，当球运行的水平距离为2.5米时，达到最大高度3.5米，然后准确落入篮圈.已知篮圈中心到地面的距离为3.05米.
(1)建立如图所示的直角坐标系，求抛物线的表达式；
(2)该运动员身高1.8米，在这次跳投中，球在头顶上方0.25米处出手，问：球出手时，他跳离地面的高度是多少。 1.如图是某公园一圆形喷水池，水流在各方向沿形状相同的抛
物线落下，如果喷头所在处A（0，1.25），水流路线最高处B
（1，2.25），则该抛物线的解析式为____________
如果不考虑其他因素，那么水池的半径至少要____米，才能使
喷出的水流不致落到池外。y= －(x-1)2 +2.252.5综合运用2.甲车在弯路作刹车试验，收集到的数据如下表所示：
(1)请用上表中的各对数据（x，y）作为点的坐标,在图所示的坐标系中画出甲车刹车距离y（米）与速度x（千米/时）的函数图象，并求函数的解析式.
（2）在一个限速为40千米/时的弯路上，甲、乙两车相向而行，同时刹车，但还是相撞了.事后测得甲、乙两车的刹车距离分别为12米和10.5米，又知乙车的刹车距离y（米）与速度x（千米/时）满足
函数 ，请你就两车的速度方面分析相撞的原因.练一练：1、一球从地面抛出的运动路线呈抛物线，如图，
当球离抛出地的水平距离为 30m 时，达到最
大高10m。
⑴ 求球运动路线的函数解析式和自变量的取值范围；
⑵ 求球被抛出多远；
⑶ 当球的高度为5m时，球离抛出地面的水平距离
是多少m？　　2.以墙为一边，用篱笆围成长方形场地，一边开2米宽的门，并用平行于一边的篱笆隔开（如图）。已知篱笆总长58米，AB长不超过8米，则这块场地的最大面积是多少？ABCD练一练：驶向胜利的彼岸今天这节课你学到什么? 谢谢！