二次函数综合应用[上学期]
图片预览







文档简介
课件21张PPT。二次函数复习——数形结合游戏规则:
1、必答题答对加10分,答错不扣分;其他大组有另外巧妙的解答,也可以加10分;
2、抢答题答对加20分,答错扣10分;
3、总结时,举手回答较好的每次加5分。
游戏结束时,总分第一名的大组每人加千分制20分,并从中评出最佳选手,另外加10分,第二名的大组每人加千分制15分,第三名的大组每人加千分制10分 (1)二次函数y=3x2-x+1的图象与x轴的交点个数是 ( ) (A) 0个 ( B )1个 (C )2个 ( D) 3个 (2) 抛物线y=3x2-x+1与坐标轴的交点共 有 ( )
( A ) 0个 ( B )1个
( C )2个 ( D ) 3个 AB一、必答题: (3) 直线y=3x+6与抛物线y=x2-x+1的交点共有( )
( A ) 0个 ( B )1个 ( C )2个 ( D )不能确定 C (4) 一元二次方程ax2+bx +c=0的两根为-3,1,则抛物线y=ax2+bx+c的对称轴是( )
(A)直线x=2 (B)直线x=-2
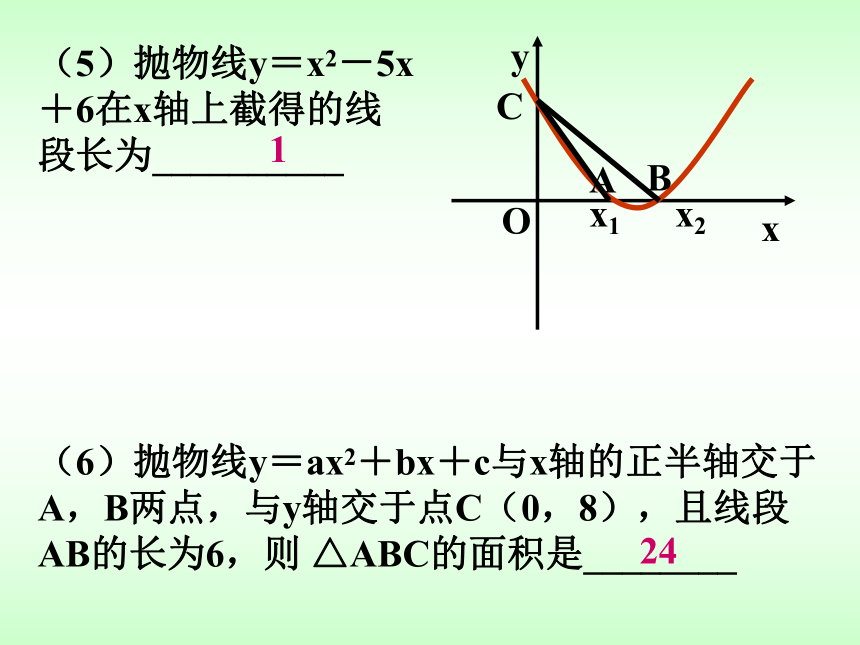
(C)直线x=1 (D)直线x=-1D(6)抛物线y=ax2+bx+c与x轴的正半轴交于A,B两点,与y轴交于点C(0,8),且线段AB的长为6,则 △ABC的面积是________24(5)抛物线y=x2-5x+6在x轴上截得的线段长为__________1 (8)二次函数y=a(x+k)2+k(a≠0),不论k为何值,图象顶点都在 ( )
(A)平分第一、三象限的一条直线上;
(B)平分第二、四象限的一条直线上;
(C)x轴上; (D)y轴上。B (7)已知:二次函数y=ax2+bx+c的图像如图,则(1)a>0; (2)b<0; (3)c<0; (4)b2-4ac >0中,正确的个数是( )
1个 (B)2个
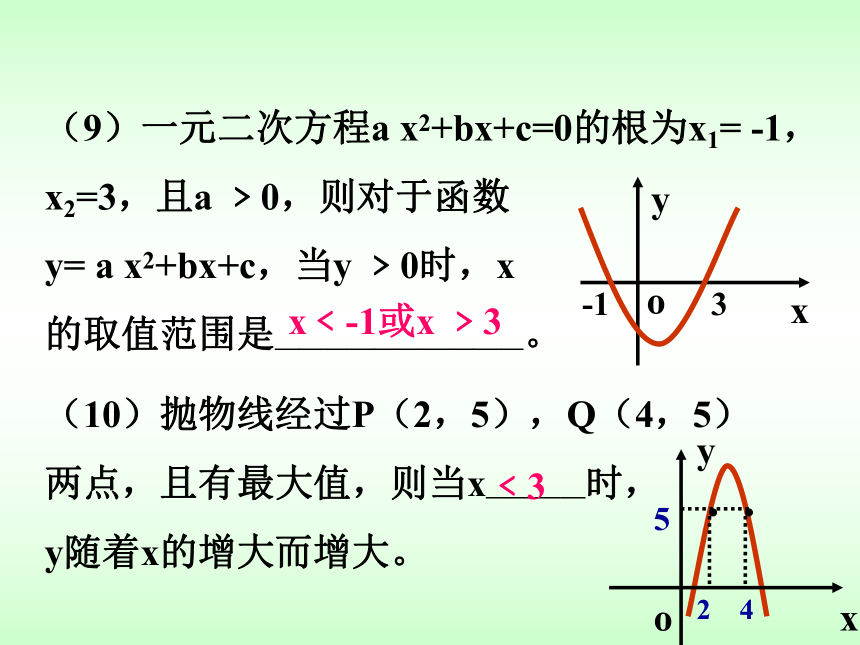
(C)3 个 (D)4个B二、抢答题(9)一元二次方程a x2+bx+c=0的根为x1= -1,
x2=3,且a ﹥0,则对于函数
y= a x2+bx+c,当y ﹥0时,x
的取值范围是——————————。x﹤-1或x ﹥3(10)抛物线经过P(2,5),Q(4,5)
两点,且有最大值,则当x————时,
y随着x的增大而增大。﹤3(11)当m_____时,抛物线y=x2+2x+m位于x轴的上方。>1(13)抛物线y=x2+bx+c交x轴于A,B两点,若点A的坐标为( 1 ,0 ),且线段AB的长为2,则 抛物线的函数解析式为(用两根式表示)____________________y=(x - 1)(x - 3)或y=(x - 1)(x + 1)(12)抛物线y=(x+3)2+k与y轴交于点(0,-2),则k=________-11(14)如果抛物线y=-x2+2(m-1)x+m+1与x轴交于A,B两点,且A点在x轴的正半轴上,B点在x轴的负半轴上,OA=a,OB=b,
(1)求m的取值范围;
(2)若a:b=3,求m的值。 (15) 如图,已知直线 y= -x+3与X轴、y轴分别交于点B、C,抛物线y= -x2+bx+c经过点B、C,点A是抛物线与x轴的另一个交点。 (1)求抛物线的解析式;解:令y=0,则 –x+3=0,x=3,∴B(3,0),令x=0, 则y=3,∴C(0,3),∴ y= -x2+2x+3(3,0)(0,3) (15)如图,已知直线 y= -x+3与X轴、y轴分别交于点B、C,抛物线y= -x2+bx+c经过点B、C,点A是抛物线与x轴的另一个交点。 (1)求抛物线的解析式;(2)若抛物线的顶点为D,求四边形ABDC的面积;(1,4)(1,0)(-1,0)解:S四边形ABDC=S△AOC+S梯形OEDC+S △EBD=9 如图,已知直线 y= -x+3与X轴、y轴分别交于点B、C,抛物线y= -x2+bx+c经过点B、C,点A是抛物线与x轴的另一个交点。 P(3,0)(0,3)xyoABCQ今天我们都学到哪些知识? 三、 如图,这是某市一处十字路口立交桥的横断面在平面直角坐标系中的示意图,横断面的地平线为x轴,横断面的对称轴为y轴。桥拱的DGD′部分为一段抛物线,顶点G的高度为8米,AD和A ′ D ′是两侧高为5.5米的支柱,OA和OA ′为两个方向的汽车通行区,宽都为15米,线段CD和C ′ D ′为两段对称的上桥斜坡,其坡度为1∶4。 (1)求桥拱DGD ′所在抛物线的解析式及CC ′的长;(0,8)(15,5.5)(-15,5.5) 如图,顶点G的高度为8米,AD和A ′ D ′是两侧高为5.5米的支柱,OA和OA ′为两个方向的汽车通行区,宽都为15米,线段CD和C ′ D ′为两段对称的上桥斜坡,其坡度为1∶4。 (2)BE和B ′E ′为支持斜坡的立柱,其高都为4米,相应的AB和A ′B ′为两个方向的行人及非机动车通行区。试求AB和A ′B ′的宽; 如图,顶点G的高度为8米,AD和A ′ D ′是两侧高为5.5米的支柱,OA和OA ′为两个方向的汽车通行区,宽都为15米,线段CD和C ′ D ′为两段对称的上桥斜坡,其坡度为1∶4。 (3)按规定,汽车通过该桥下时,载货最高处和桥拱之间的距离不得小于0.4米。今有一大型运货汽车,装载某大型设备后,其宽为4米,车载大型设备的顶部与地面的距离均为7米。它能否从OA(或OA ′)区域安全通过?请说明理由。B6、已知:如图,抛物线与轴的负半轴交于C点,ACB=90,且=,求ABC的面积。
1、必答题答对加10分,答错不扣分;其他大组有另外巧妙的解答,也可以加10分;
2、抢答题答对加20分,答错扣10分;
3、总结时,举手回答较好的每次加5分。
游戏结束时,总分第一名的大组每人加千分制20分,并从中评出最佳选手,另外加10分,第二名的大组每人加千分制15分,第三名的大组每人加千分制10分 (1)二次函数y=3x2-x+1的图象与x轴的交点个数是 ( ) (A) 0个 ( B )1个 (C )2个 ( D) 3个 (2) 抛物线y=3x2-x+1与坐标轴的交点共 有 ( )
( A ) 0个 ( B )1个
( C )2个 ( D ) 3个 AB一、必答题: (3) 直线y=3x+6与抛物线y=x2-x+1的交点共有( )
( A ) 0个 ( B )1个 ( C )2个 ( D )不能确定 C (4) 一元二次方程ax2+bx +c=0的两根为-3,1,则抛物线y=ax2+bx+c的对称轴是( )
(A)直线x=2 (B)直线x=-2
(C)直线x=1 (D)直线x=-1D(6)抛物线y=ax2+bx+c与x轴的正半轴交于A,B两点,与y轴交于点C(0,8),且线段AB的长为6,则 △ABC的面积是________24(5)抛物线y=x2-5x+6在x轴上截得的线段长为__________1 (8)二次函数y=a(x+k)2+k(a≠0),不论k为何值,图象顶点都在 ( )
(A)平分第一、三象限的一条直线上;
(B)平分第二、四象限的一条直线上;
(C)x轴上; (D)y轴上。B (7)已知:二次函数y=ax2+bx+c的图像如图,则(1)a>0; (2)b<0; (3)c<0; (4)b2-4ac >0中,正确的个数是( )
1个 (B)2个
(C)3 个 (D)4个B二、抢答题(9)一元二次方程a x2+bx+c=0的根为x1= -1,
x2=3,且a ﹥0,则对于函数
y= a x2+bx+c,当y ﹥0时,x
的取值范围是——————————。x﹤-1或x ﹥3(10)抛物线经过P(2,5),Q(4,5)
两点,且有最大值,则当x————时,
y随着x的增大而增大。﹤3(11)当m_____时,抛物线y=x2+2x+m位于x轴的上方。>1(13)抛物线y=x2+bx+c交x轴于A,B两点,若点A的坐标为( 1 ,0 ),且线段AB的长为2,则 抛物线的函数解析式为(用两根式表示)____________________y=(x - 1)(x - 3)或y=(x - 1)(x + 1)(12)抛物线y=(x+3)2+k与y轴交于点(0,-2),则k=________-11(14)如果抛物线y=-x2+2(m-1)x+m+1与x轴交于A,B两点,且A点在x轴的正半轴上,B点在x轴的负半轴上,OA=a,OB=b,
(1)求m的取值范围;
(2)若a:b=3,求m的值。 (15) 如图,已知直线 y= -x+3与X轴、y轴分别交于点B、C,抛物线y= -x2+bx+c经过点B、C,点A是抛物线与x轴的另一个交点。 (1)求抛物线的解析式;解:令y=0,则 –x+3=0,x=3,∴B(3,0),令x=0, 则y=3,∴C(0,3),∴ y= -x2+2x+3(3,0)(0,3) (15)如图,已知直线 y= -x+3与X轴、y轴分别交于点B、C,抛物线y= -x2+bx+c经过点B、C,点A是抛物线与x轴的另一个交点。 (1)求抛物线的解析式;(2)若抛物线的顶点为D,求四边形ABDC的面积;(1,4)(1,0)(-1,0)解:S四边形ABDC=S△AOC+S梯形OEDC+S △EBD=9 如图,已知直线 y= -x+3与X轴、y轴分别交于点B、C,抛物线y= -x2+bx+c经过点B、C,点A是抛物线与x轴的另一个交点。 P(3,0)(0,3)xyoABCQ今天我们都学到哪些知识? 三、 如图,这是某市一处十字路口立交桥的横断面在平面直角坐标系中的示意图,横断面的地平线为x轴,横断面的对称轴为y轴。桥拱的DGD′部分为一段抛物线,顶点G的高度为8米,AD和A ′ D ′是两侧高为5.5米的支柱,OA和OA ′为两个方向的汽车通行区,宽都为15米,线段CD和C ′ D ′为两段对称的上桥斜坡,其坡度为1∶4。 (1)求桥拱DGD ′所在抛物线的解析式及CC ′的长;(0,8)(15,5.5)(-15,5.5) 如图,顶点G的高度为8米,AD和A ′ D ′是两侧高为5.5米的支柱,OA和OA ′为两个方向的汽车通行区,宽都为15米,线段CD和C ′ D ′为两段对称的上桥斜坡,其坡度为1∶4。 (2)BE和B ′E ′为支持斜坡的立柱,其高都为4米,相应的AB和A ′B ′为两个方向的行人及非机动车通行区。试求AB和A ′B ′的宽; 如图,顶点G的高度为8米,AD和A ′ D ′是两侧高为5.5米的支柱,OA和OA ′为两个方向的汽车通行区,宽都为15米,线段CD和C ′ D ′为两段对称的上桥斜坡,其坡度为1∶4。 (3)按规定,汽车通过该桥下时,载货最高处和桥拱之间的距离不得小于0.4米。今有一大型运货汽车,装载某大型设备后,其宽为4米,车载大型设备的顶部与地面的距离均为7米。它能否从OA(或OA ′)区域安全通过?请说明理由。B6、已知:如图,抛物线与轴的负半轴交于C点,ACB=90,且=,求ABC的面积。
同课章节目录
