2.3二次函数的性质[上学期]

2.3二次函数的性质
教学目标:1.从具体函数的图象中认识二次函数的基本性质.
2.了解二次函数与二次方程的相互关系.
3.探索二次函数的变化规律,掌握函数的最大值(或最小值)及函数的增减性的概念,会求二次函数的最值,并能根据性质判断函数在某一范围内的增减性
重点:二次函数的最大值,最小值及增减性的理解和求法.
难点:二次函数的性质的应用.
教学过程:
1. 复习引入
二次函数: y=ax2 +bx + c (a 0)的图象是一条抛物线,它的开口由什么决定呢
补充: 当a的绝对值相等时,其形状完全相同,当a的绝对值越大,则开口越小,反之成立.
二,新课教学:
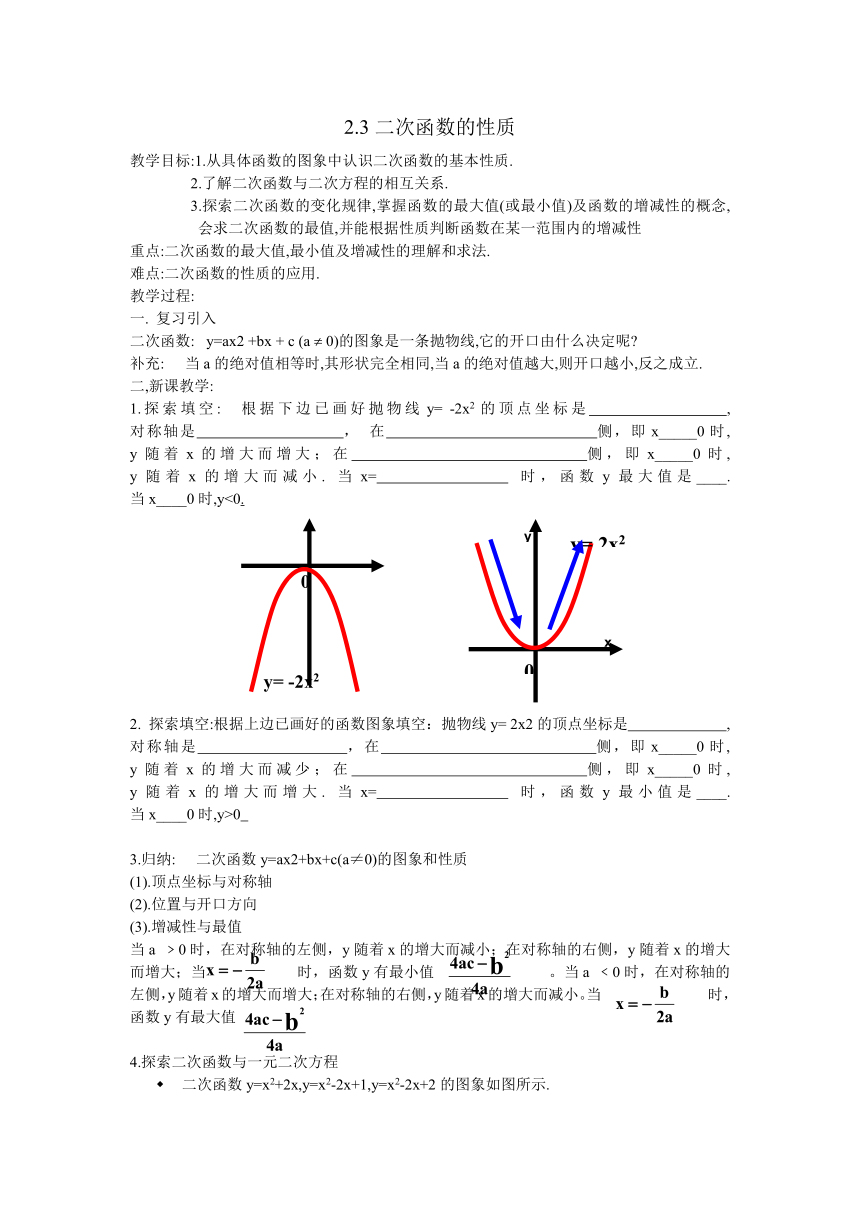
1.探索填空: 根据下边已画好抛物线y= -2x2的顶点坐标是 , 对称轴是 ， 在 侧，即x_____0时, y随着x的增大而增大；在 侧，即x_____0时, y随着x的增大而减小. 当x= 时，函数y最大值是____. 当x____0时,y<0.
2. 探索填空:根据上边已画好的函数图象填空： 抛物线y= 2x2的顶点坐标是 , 对称轴是 ，在 侧，即x_____0时, y随着x的增大而减少；在 侧，即x_____0时, y随着x的增大而增大. 当x= 时，函数y最小值是____. 当x____0时,y>0
3.归纳: 二次函数y=ax2+bx+c(a≠0)的图象和性质
(1).顶点坐标与对称轴
(2).位置与开口方向
(3).增减性与最值
当a ﹥0时，在对称轴的左侧，y随着x的增大而减小；在对称轴的右侧，y随着x的增大而增大；当 时，函数y有最小值 。当a ﹤0时，在对称轴的左侧，y随着x的增大而增大；在对称轴的右侧，y随着x的增大而减小。当 时，函数y有最大值
4.探索二次函数与一元二次方程
二次函数y=x2+2x,y=x2-2x+1,y=x2-2x+2的图象如图所示.
(1).每个图象与x轴有几个交点？
(2).一元二次方程x2+2x=0,x2-2x+1=0有几个根 验证一下一元二次方程x2-2x+2=0有根吗
(3).二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系
归纳: (3).二次函数y=ax2+bx+c的图象和x轴交点有三种情况:
①有两个交点,
②有一个交点,
③没有交点.
当二次函数y=ax2+bx+c的图象和x轴有交点时, 交点的横坐标就是当y=0时自变量x的值,即一元二次方程ax2+bx+c=0的根.
当b2-4ac﹥0时，抛物线与x轴有两个交点，交点的横坐标是一元二次方程0=ax2+bx+c的两个根x1与 x2；当b2-4ac=0时，抛物线与x轴有且只有一个公共点；当b2-4ac﹤0时，抛物线与x轴没有交点。
举例: 求二次函数图象y=x2-3x+2与x轴的交点A、B的坐标。
结论1：方程x2-3x+2=0的解就是抛物线y=x2-3x+2与x轴的两个交点的横坐标。因此，抛物线与一元二次方程是有密切联系的。
即：若一元二次方程ax2+bx+c=0的两个根是x1、x2，则抛物线y=ax2+bx+c与轴的两个交点坐标分别是A（ x1，0），B（x2,0）
5.例题教学:例1: 已知函数
⑴写出函数图像的顶点、图像与坐标轴的交点，以及图像与y轴的交点关于图象对称轴的对称点。然后画出函数图像的草图；
(2)自变量x在什么范围内时， y随着x的增大而增大？何时y随着x的增大而减少；并求出函数的最大值或最小值。
归纳:二次函数五点法的画法
例２　　已知函数y= x2 -2x -3 ,
（１）写出函数图象的顶点、图象与坐标轴的交点，以及图象与 y 轴的交点关于图象对称轴的对称点。然后画出函数图象的草图；
(2)求图象与坐标轴交点构成的三角形 的面积：
（3）根据第（１）题的图象草图，说 出 x 取哪些值时， ① y=0; ② y<0; ③ y>0.
三.巩固练习: 请完成课本练习：p42. 1,2
四.尝试提高:1、二次函数y=ax2+bx+c(a≠0)的图象如图所示，
则a、b、c的符号为__________.
2、已知二次函数的图像如图所示，下列结论：
⑴a+b+c﹤0 ⑵a-b+c﹥0 ⑶abc ﹥0 ⑷b=2a
其中正确的结论的个数是（ ）A 1个 B 2个 C 3个 D 4个
五.学习感想: 1、你能正确地说出二次函数的性质吗？
2、你能用“五点法”快速地画出二次函数的图象吗？你能利用函数图象回答有关性质吗？
作业:作业本,课本练习
x
y
y= -2x2
0
y= 2x2
0
o
x
y
y
0
1
-1
x