圆内接四边形[上学期]

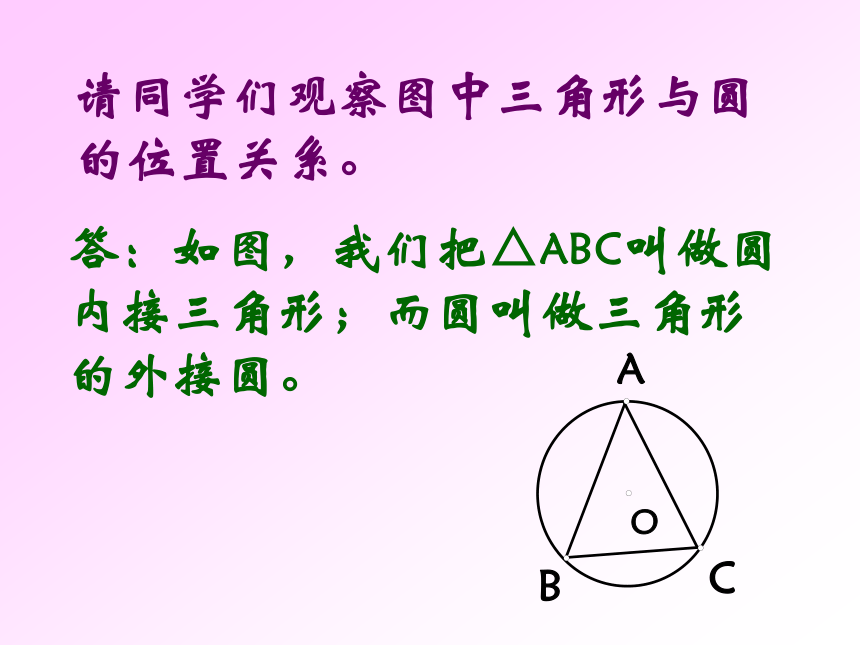
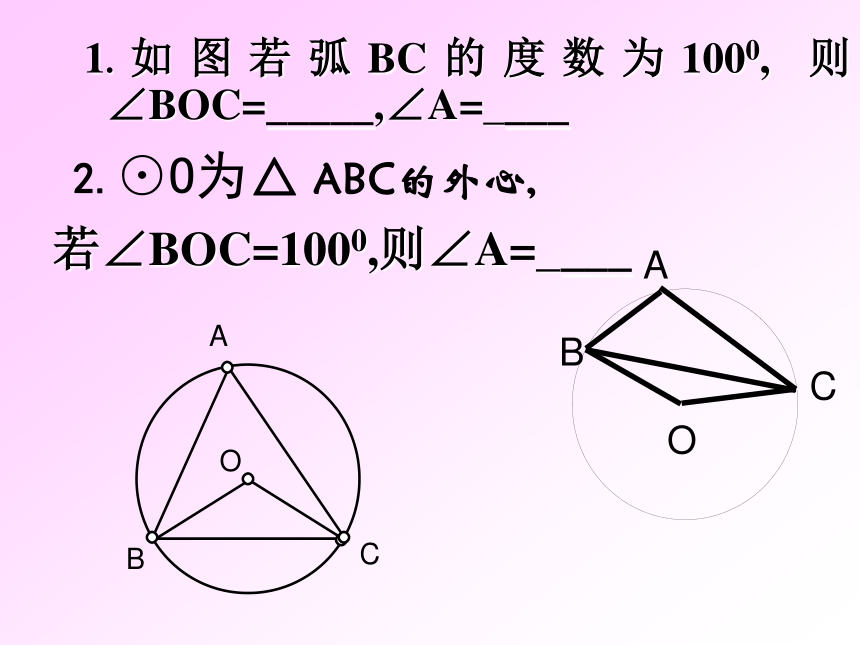
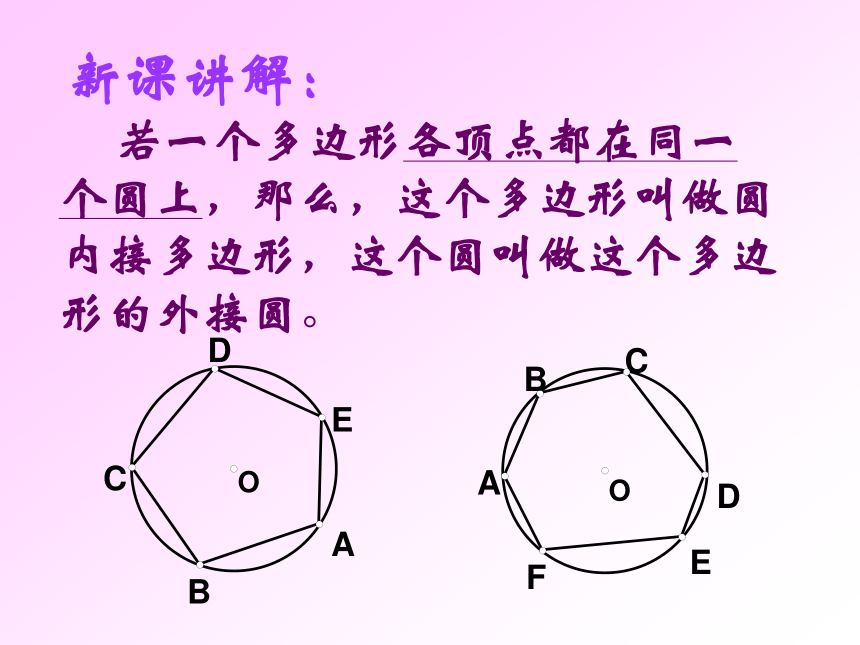
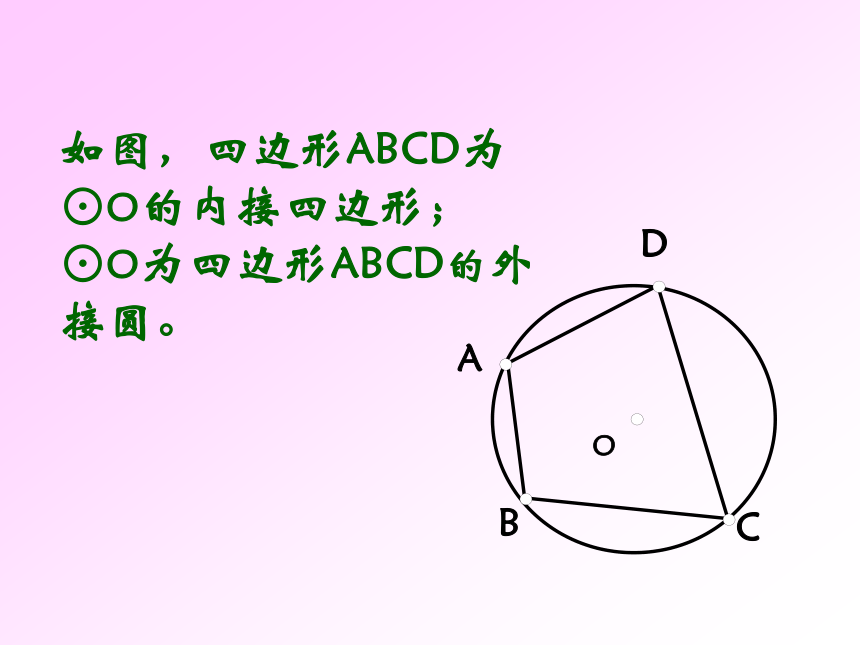
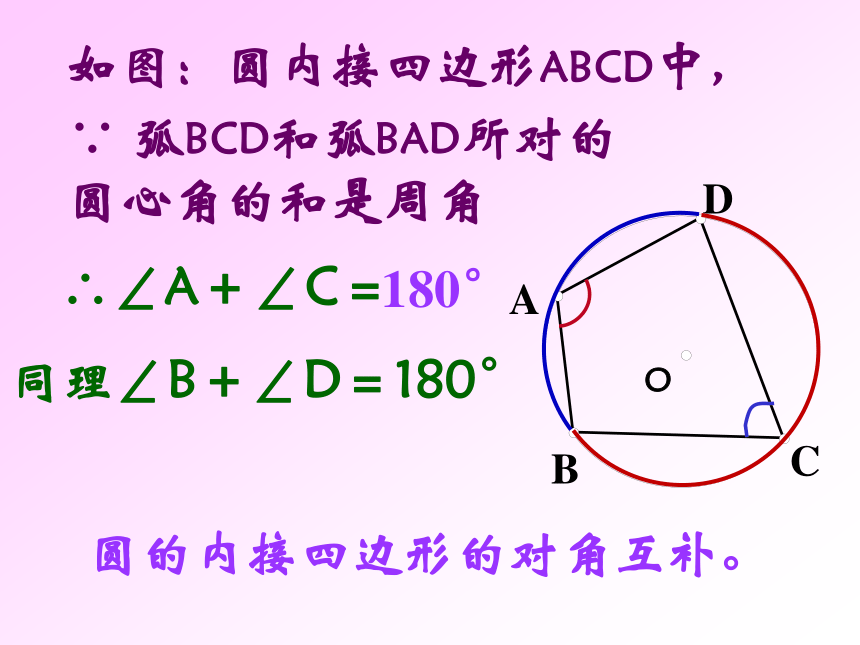
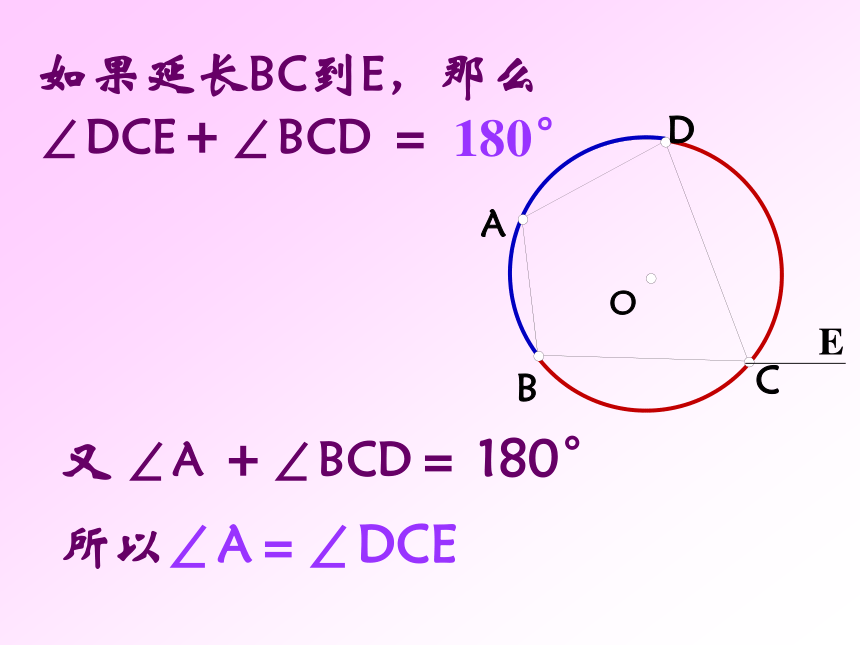
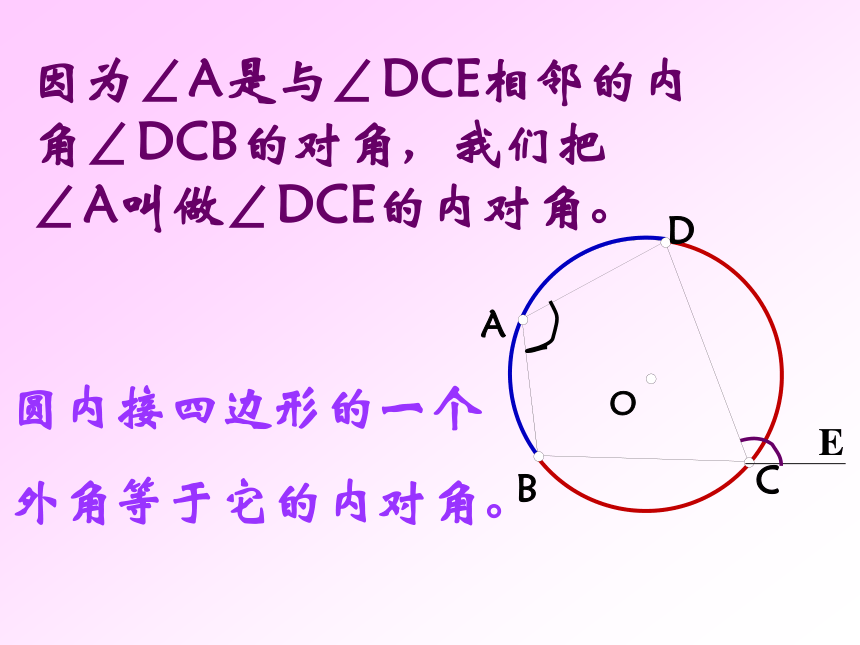
课件31张PPT。圆内接四边形请同学们观察图中三角形与圆的位置关系。答：如图，我们把△ABC叫做圆内接三角形；而圆叫做三角形的外接圆。 1.如图若弧BC的度数为1000, 则∠BOC=_____,∠A= ___ 若∠BOC=1000,则∠A= ___ 2.⊙O为△ ABC的外心, 新课讲解： 若一个多边形各顶点都在同一个圆上，那么，这个多边形叫做圆内接多边形，这个圆叫做这个多边形的外接圆。OACDEB如图，四边形ABCD为⊙O的内接四边形；⊙O为四边形ABCD的外接圆。 CODBA如图：圆内接四边形ABCD中，∵ 弧BCD和弧BAD所对的圆心角的和是周角∴∠A＋∠C＝180° 同理∠B＋∠D＝180°圆的内接四边形的对角互补。如果延长BC到E，那么∠DCE＋∠BCD ＝180°所以∠A＝∠DCE又 ∠A ＋∠BCD＝ 180°因为∠A是与∠DCE相邻的内角∠DCB的对角，我们把∠A叫做∠DCE的内对角。圆内接四边形的一个
外角等于它的内对角。定理： 圆的内接四边形的对角互补，并且任何一个外角都等于它的内对角。CODBA练一练1圆内接四边形ABCD中, ∠A =500, ∠C=___2.圆内接四边形ABCD中,
∠A :∠B :∠C: =3:5:6,
则∠D=____3.圆内接四边形ABCD中,
∠A :∠B :∠C: :∠D =3:5:6:n
则n=____,最大内角=____4.若ABCD为圆内接四边形，则下列哪个选项可能成立（ ）（A）∠A∶∠B∶∠C∶∠D ＝ 1∶2∶3∶4 （B）∠A∶∠B∶∠C∶∠D ＝ 2∶1∶3∶4 （C）∠A∶∠B∶∠C∶∠D ＝ 3∶2∶1∶4 （D）∠A∶∠B∶∠C∶∠D ＝ 4∶3∶2∶1B练一练5.如图, ∠AOC=1400,B是AC上的任一点, ∠ABC=____
BCAO⌒P练一练6. ⊙O 2过⊙O1的圆心
∠C=500, 则∠D=___
ACBO1O2D10. 梯形ABCD内接于⊙O,AD∥BC, ∠B=750,则∠C=_____ 8 圆的内接菱形一定是＿＿＿形。7.圆的内接平行四边形一定是＿＿形。9 圆的内接梯形一定是＿＿＿梯形。ABE 例题1:
AD是△ABC的外角
∠EAC的平分线,
与△ABC的外接圆
交于点D.
求证:DB=DCDCABE 两圆交于A,B两点
BA是 ⊙O1的直径,交
⊙O2于点D,连BE交
⊙O2于点C
求证: ∠D=900DCO1O2例 2: 如图⊙O1与⊙O2都经过A、B两点，经过点A的直线CD与⊙O1 交于点C，与⊙O2 交于点D。经过点B的直线EF与⊙O1 交于点E，与⊙O2 交于点F。
求证：CE∥DFCE∥DF1∠E＋∠F＝180°∠E＋∠1＝180°、∠1＝∠F连结ABFABEO1 CE//DF
还成立吗?
FDCO2ABEF
求证:
∠C+ ∠MEN
=1800
MNDCBo1o2“四点共圆”
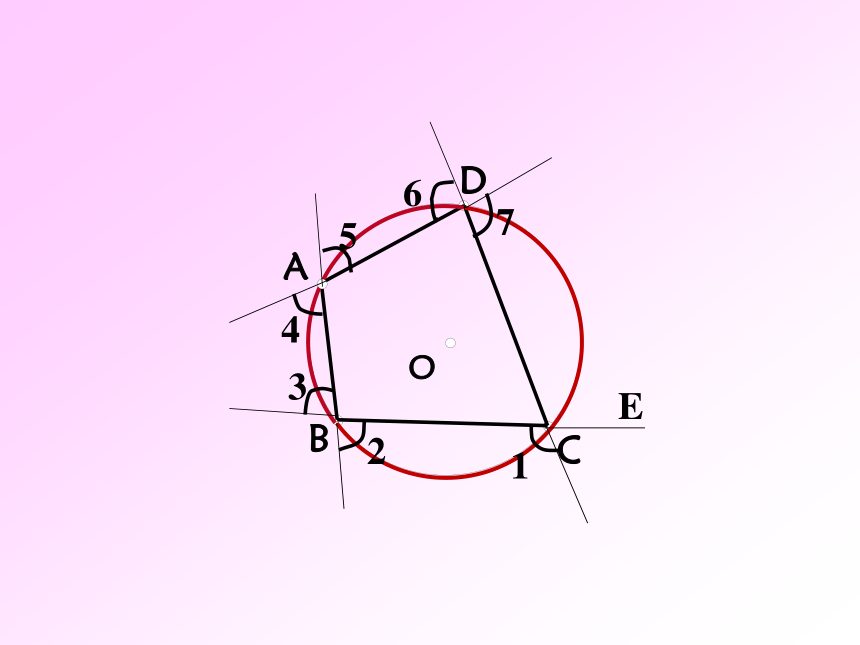
判定四点共圆常用方法：1、到定点的距离等于定长的四点；
2、对角互补的四边形，
3, 外角等于内对角的四边形；
4、在一条线段的同侧两个张角相等的四点；
ACDB矩形，正方形，等腰梯形，一定有外接圆再见ABEO 1.⊙O弦AB⊥CD
于E,AE=2,BE=6
ED=3,EC=4
求 ⊙O的半径
MNDC提高练习1。平分弦的直线必过圆心（ ）
2。平分弧的直线也平分
这条弧所对的弦（ ）ABEO 2.⊙O弦AB⊥CD
OE⊥AD于E
求证：BC=2OEFDCFABEO 3.AB是⊙O的直径
弦CD⊥AB于E,G是
AC上的任一点
延长AG与DC的延
长线交于F
求证:
∠FGC=∠AGD
DCFG⌒ODCBA5.弓形的弦AB=8
弓高CD=2,弓形所在圆的半径是
————6.弓形的弦4
弓形所在圆的半径是7,则弓形的高是
————