3.2三角形的内切圆[上学期]
图片预览


文档简介
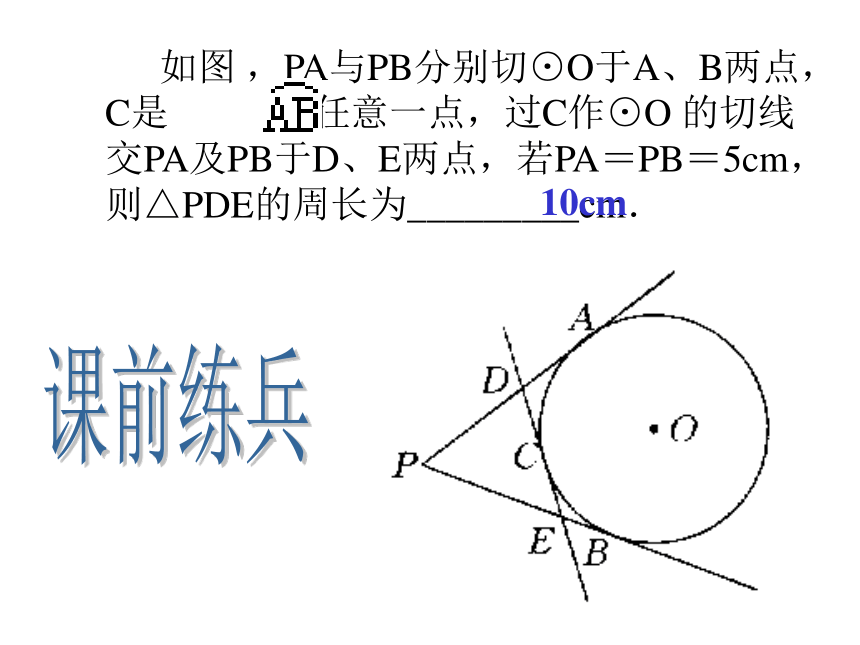
课件20张PPT。三角形的内切圆 如图 ,PA与PB分别切⊙O于A、B两点,C是 上任意一点,过C作⊙O 的切线交PA及PB于D、E两点,若PA=PB=5cm,则△PDE的周长为_________cm.10cm课前练兵切线长定理:
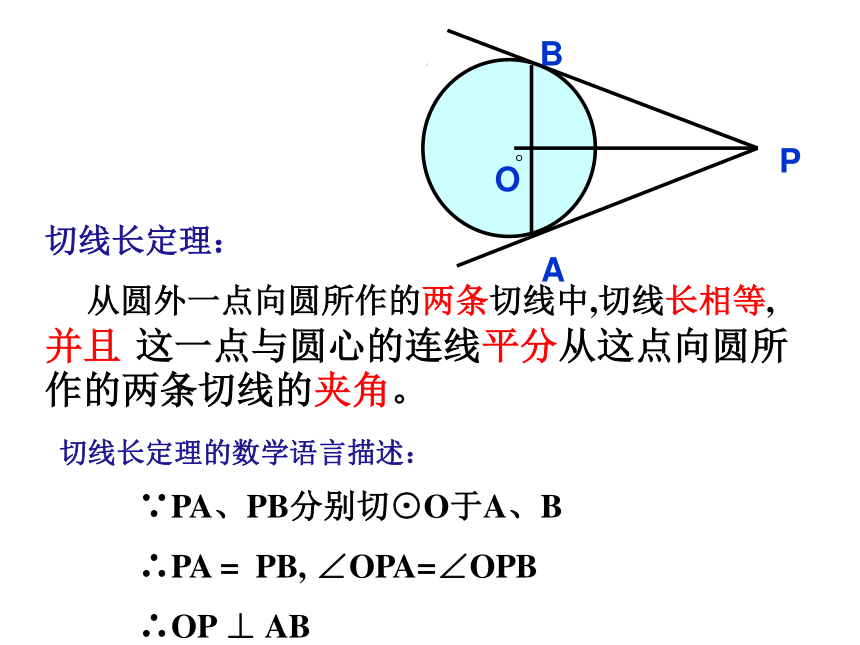
从圆外一点向圆所作的两条切线中,切线长相等,并且 这一点与圆心的连线平分从这点向圆所作的两条切线的夹角。 ∵PA、PB分别切⊙O于A、B
∴PA = PB, ∠OPA=∠OPB
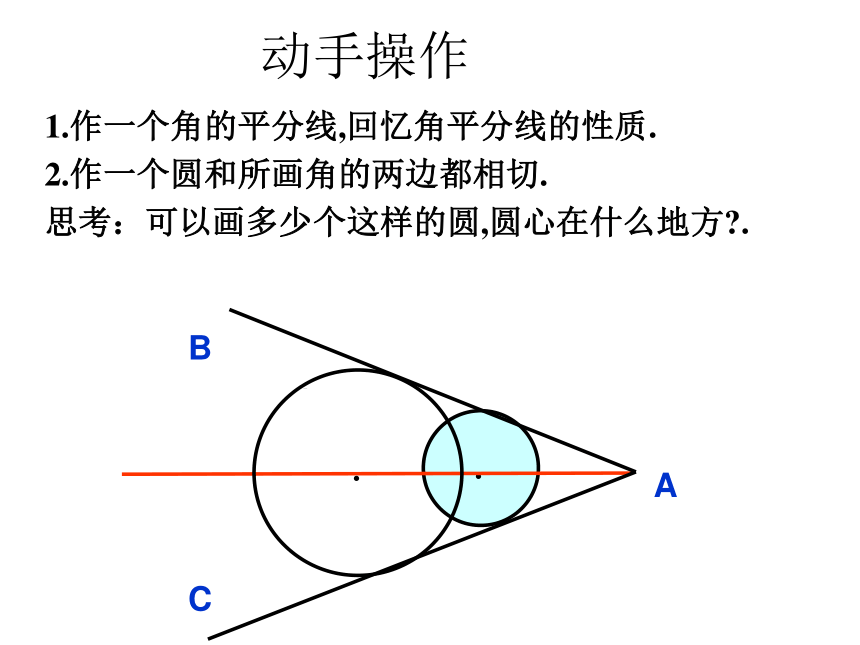
∴OP ⊥ AB切线长定理的数学语言描述: 三角形的内切圆动手操作1.作一个角的平分线,回忆角平分线的性质.
2.作一个圆和所画角的两边都相切.
思考:可以画多少个这样的圆,圆心在什么地方?.
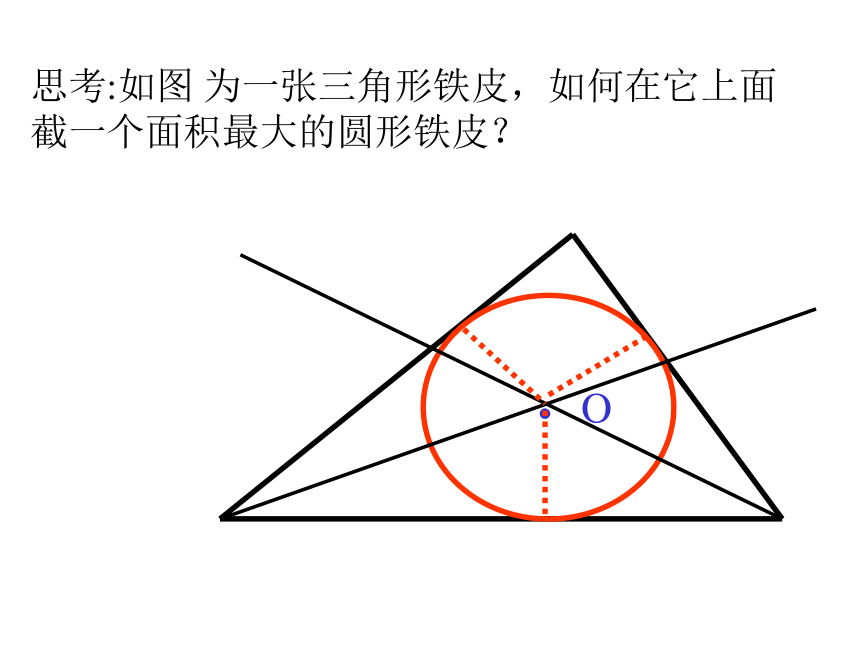
·思考:如图 为一张三角形铁皮,如何在它上面截一个面积最大的圆形铁皮? ?
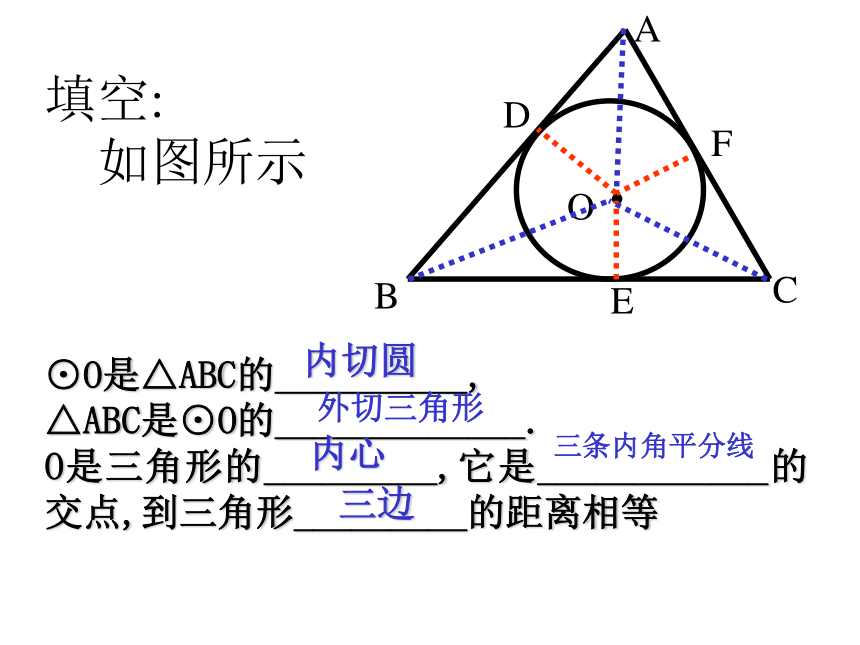
O填空: 如图所示⊙O是△ABC的__________,
△ABC是⊙O的_____________.
O是三角形的_________,它是____________的交点,到三角形_________的距离相等内切圆外切三角形 内心三边三条内角平分线 DEF 1. 三角形的内切圆能作____个,圆的外切三角形有_____ 个,三角形的内心在圆的_______.
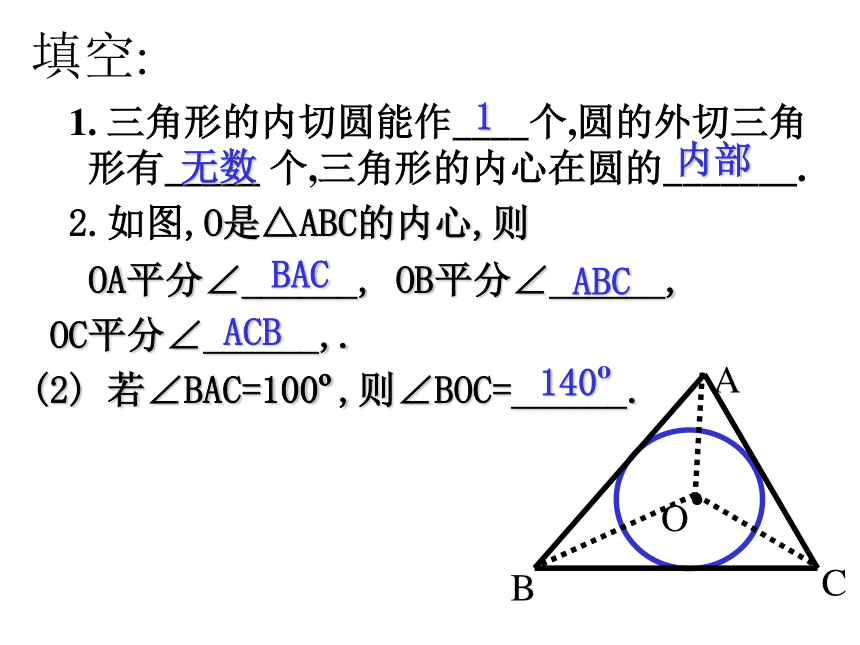
2.如图,O是△ABC的内心,则
OA平分∠______, OB平分∠______,
OC平分∠______,.
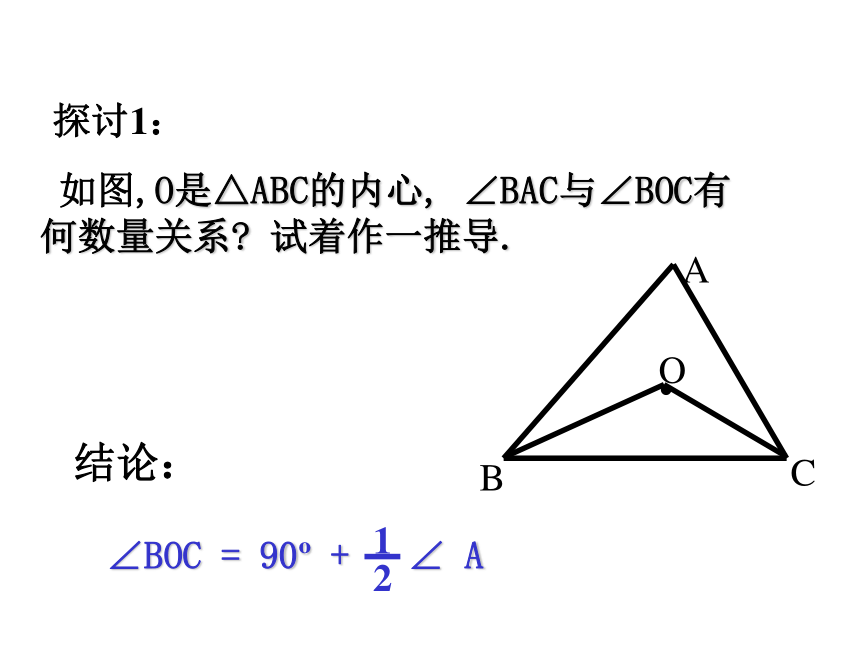
(2) 若∠BAC=100o,则∠BOC=______.填空:1无数内部 BAC 140o ABC ACB 如图,O是△ABC的内心, ∠BAC与∠BOC有何数量关系? 试着作一推导.探讨1:
结论:探讨2:
设△ABC 的内切圆的半径为r,△ABC 的各边长之和为L,△ABC 的面积S,我们会有什么结论?
解:AD+AF+BD+BE+CE+CF=L
2AD+2BE+2CE=L
2AD=L-2(BE+CE)
AD=AE=?
BD=BE?
CE=CF=?
CDEF三角形面积
(L为三角形周长,r为内切圆半径)rOBA? 探讨3:
设△ABC是直角三角形,∠C=90°,它
的内切圆的半径为r,△ABC 的各边长分别为a、b、c,试探讨r与a、b、c的关系.
C┛cbaFEDr结论:变式练习1 在RT△ABC中,∠C=90o,AC=3,BC=4,则RT△ABC的内切圆的半径为=_________.B1 若直角三角形斜边长为10cm,其内切圆的半径为2cm,则它的周长为( )
A.24cm B.22cm
C.14cm D.12cm变式练习2A小结1: 三角形的内切圆
(1)三角形的内心是三角形内切圆的圆心
(2)三角形的内心是三角形各角平分线的交点
(3)三角形内心到三边的距离相等
(4)三角形面积 (C为三角形周长,
r为内切圆半径)(5)直角三角形 的内切圆的半径为r 与 各边长 a、b、c的关系是练 习1. 如图,⊙O是△ABC 的内切圆,与AB、BC、CA分别切于点D、E、F,∠DOE=120°,∠EOF=150°,则∠A=_______,∠B=_______, ∠C= _________.
2.? △ABC 的内切圆⊙O 与AB 、 BC 、 AC分别相切于点D、E、F,且AB=5厘米,BC=9厘米,AC=6厘米,则AD=______,BE=_______,CF=______.
1厘米4厘米5厘米3.要在如图所示的三条公路旁修建一加油站P,使加油站P到三条公路的距离相等.你认为加油站应修于何处?·O4.等边三角形内切圆和外接圆半径之比为( )
A. B. C. D.B5.下列说法:
(1)任意一个三角形一定有一个外接圆,并且只有一个外接圆.
(2)任意一个圆一定有一个内接三角形,并且只有一个内接三角形.
(3)任意一个三角形一定有一个内切圆,并且只有一个内切圆.
(4)任意一个圆一定有一个外切三角形,并且只有一个外切三角形
正确说法有( )个
A 1 B 2 C 3 D 4 小结2: 三角形外心、内心有关知识比较三边垂直平分线三个内角的平分线
从圆外一点向圆所作的两条切线中,切线长相等,并且 这一点与圆心的连线平分从这点向圆所作的两条切线的夹角。 ∵PA、PB分别切⊙O于A、B
∴PA = PB, ∠OPA=∠OPB
∴OP ⊥ AB切线长定理的数学语言描述: 三角形的内切圆动手操作1.作一个角的平分线,回忆角平分线的性质.
2.作一个圆和所画角的两边都相切.
思考:可以画多少个这样的圆,圆心在什么地方?.
·思考:如图 为一张三角形铁皮,如何在它上面截一个面积最大的圆形铁皮? ?
O填空: 如图所示⊙O是△ABC的__________,
△ABC是⊙O的_____________.
O是三角形的_________,它是____________的交点,到三角形_________的距离相等内切圆外切三角形 内心三边三条内角平分线 DEF 1. 三角形的内切圆能作____个,圆的外切三角形有_____ 个,三角形的内心在圆的_______.
2.如图,O是△ABC的内心,则
OA平分∠______, OB平分∠______,
OC平分∠______,.
(2) 若∠BAC=100o,则∠BOC=______.填空:1无数内部 BAC 140o ABC ACB 如图,O是△ABC的内心, ∠BAC与∠BOC有何数量关系? 试着作一推导.探讨1:
结论:探讨2:
设△ABC 的内切圆的半径为r,△ABC 的各边长之和为L,△ABC 的面积S,我们会有什么结论?
解:AD+AF+BD+BE+CE+CF=L
2AD+2BE+2CE=L
2AD=L-2(BE+CE)
AD=AE=?
BD=BE?
CE=CF=?
CDEF三角形面积
(L为三角形周长,r为内切圆半径)rOBA? 探讨3:
设△ABC是直角三角形,∠C=90°,它
的内切圆的半径为r,△ABC 的各边长分别为a、b、c,试探讨r与a、b、c的关系.
C┛cbaFEDr结论:变式练习1 在RT△ABC中,∠C=90o,AC=3,BC=4,则RT△ABC的内切圆的半径为=_________.B1 若直角三角形斜边长为10cm,其内切圆的半径为2cm,则它的周长为( )
A.24cm B.22cm
C.14cm D.12cm变式练习2A小结1: 三角形的内切圆
(1)三角形的内心是三角形内切圆的圆心
(2)三角形的内心是三角形各角平分线的交点
(3)三角形内心到三边的距离相等
(4)三角形面积 (C为三角形周长,
r为内切圆半径)(5)直角三角形 的内切圆的半径为r 与 各边长 a、b、c的关系是练 习1. 如图,⊙O是△ABC 的内切圆,与AB、BC、CA分别切于点D、E、F,∠DOE=120°,∠EOF=150°,则∠A=_______,∠B=_______, ∠C= _________.
2.? △ABC 的内切圆⊙O 与AB 、 BC 、 AC分别相切于点D、E、F,且AB=5厘米,BC=9厘米,AC=6厘米,则AD=______,BE=_______,CF=______.
1厘米4厘米5厘米3.要在如图所示的三条公路旁修建一加油站P,使加油站P到三条公路的距离相等.你认为加油站应修于何处?·O4.等边三角形内切圆和外接圆半径之比为( )
A. B. C. D.B5.下列说法:
(1)任意一个三角形一定有一个外接圆,并且只有一个外接圆.
(2)任意一个圆一定有一个内接三角形,并且只有一个内接三角形.
(3)任意一个三角形一定有一个内切圆,并且只有一个内切圆.
(4)任意一个圆一定有一个外切三角形,并且只有一个外切三角形
正确说法有( )个
A 1 B 2 C 3 D 4 小结2: 三角形外心、内心有关知识比较三边垂直平分线三个内角的平分线
