圆的基本性质复习课[上学期]

课件24张PPT。第3章圆的基本性质
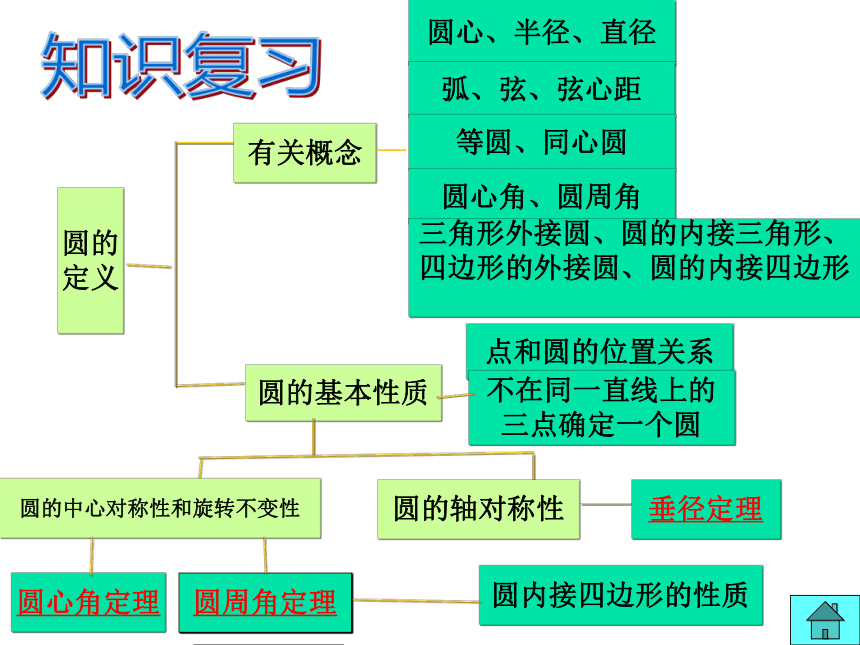
复习课（1）知识复习圆的
定义有关概念圆的基本性质圆心、半径、直径弧、弦、弦心距等圆、同心圆圆心角、圆周角三角形外接圆、圆的内接三角形、
四边形的外接圆、圆的内接四边形
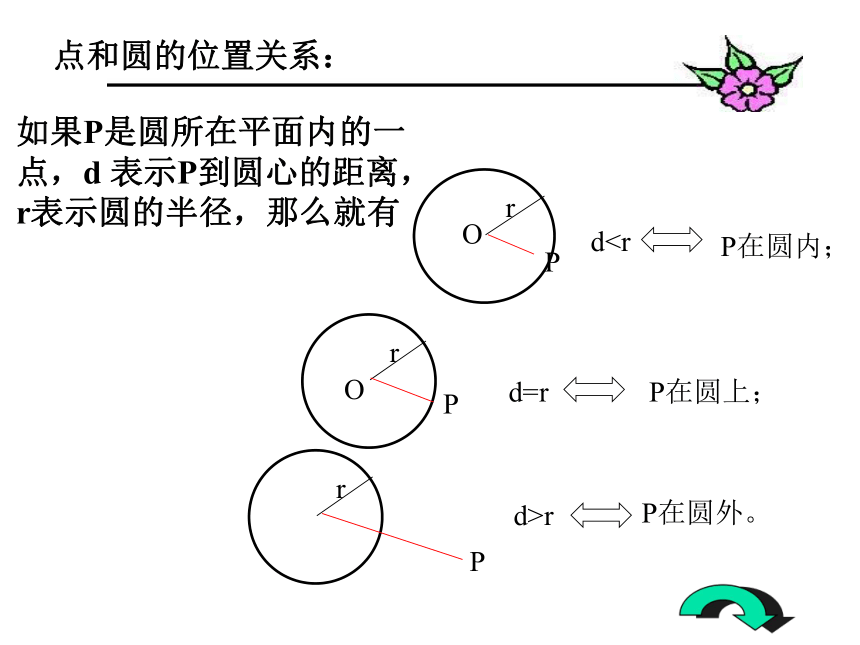
点和圆的位置关系不在同一直线上的
三点确定一个圆圆的中心对称性和旋转不变性圆的轴对称性垂径定理圆心角定理圆周角定理圆内接四边形的性质如果P是圆所在平面内的一
点，d 表示P到圆心的距离，
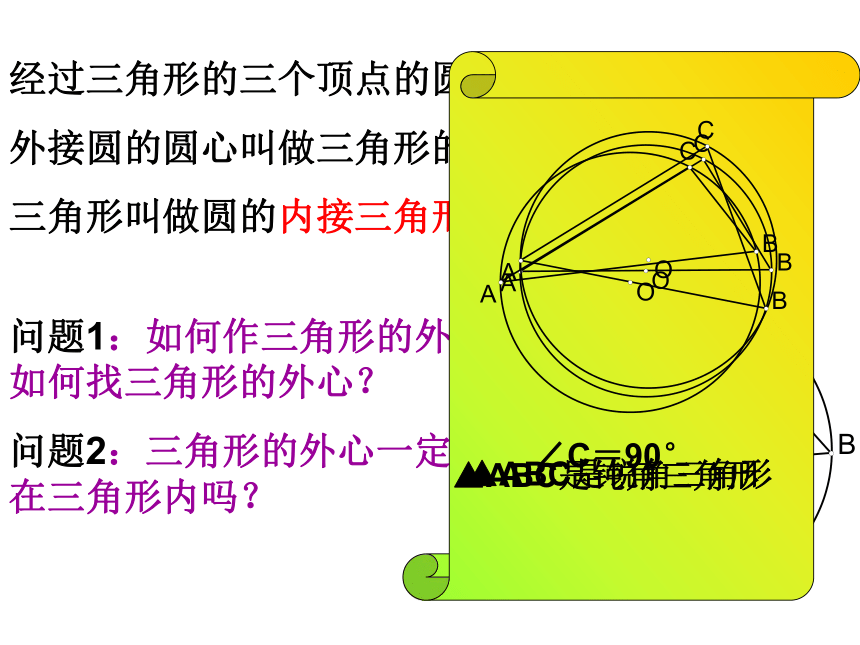
r表示圆的半径，那么就有drP在圆外。点和圆的位置关系：问题：（1）经过一个已知点可以画多少个圆？（2）经过两个已知点可以画多少个圆？这样的圆的圆心在怎样的一条直线上？（3）过同在一条直线上的三个点能画圆吗？定理：不在同一直线上的三个点
确定一个圆。经过三角形的三个顶点的圆叫做三角形的外接圆，
外接圆的圆心叫做三角形的外心，
三角形叫做圆的内接三角形。问题1：如何作三角形的外接圆？如何找三角形的外心？
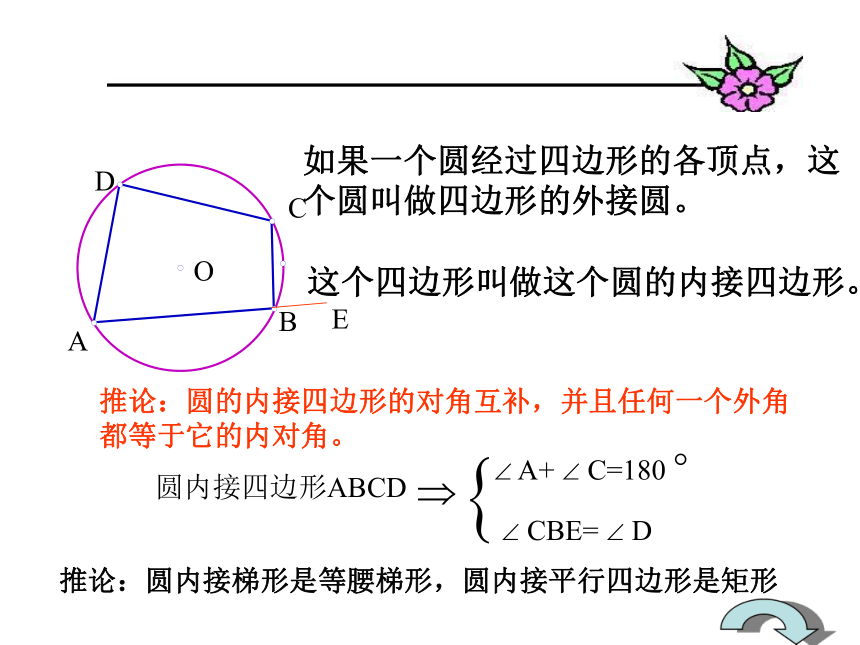
问题2：三角形的外心一定 在三角形内吗？∠C＝90°▲ABC是锐角三角形▲ABC是钝角三角形如果一个圆经过四边形的各顶点，这
个圆叫做四边形的外接圆。 这个四边形叫做这个圆的内接四边形。推论：圆的内接四边形的对角互补，并且任何一个外角
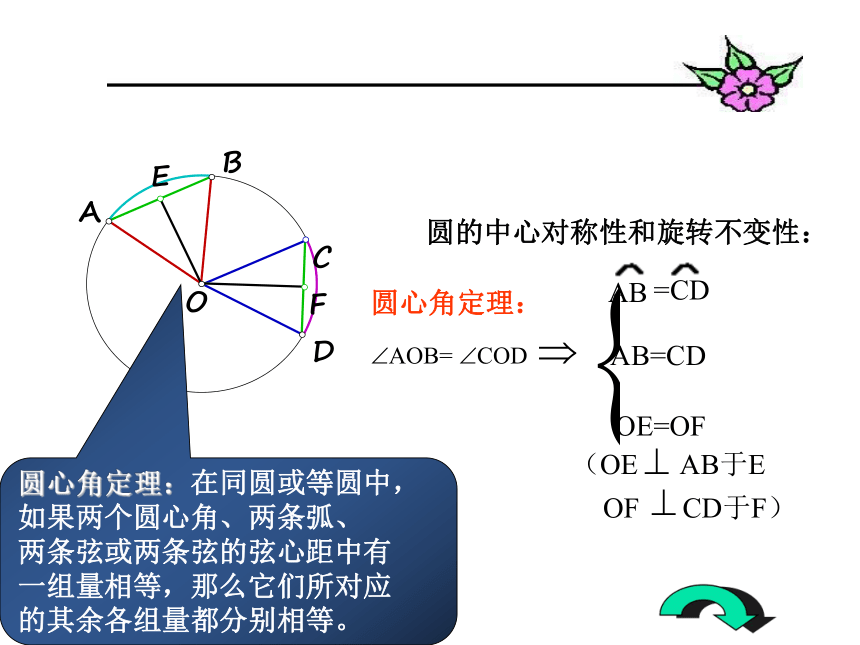
都等于它的内对角。圆内接四边形ABCD? A+ ? C=180 ?? CBE= ? DODABCE推论：圆内接梯形是等腰梯形，圆内接平行四边形是矩形ODCBAFE圆的中心对称性和旋转不变性：圆心角定理：?AOB= ?CODAB=CDAB=CDOE=OF（OE AB于EOF CD于F）圆心角定理：在同圆或等圆中，
如果两个圆心角、两条弧、
两条弦或两条弦的弦心距中有
一组量相等，那么它们所对应
的其余各组量都分别相等。圆周角定理： 一条弧所对的圆周角等于它所对的圆心角的一半。推论：
半圆（或直径）所对的圆周角是直角，
90?圆周角所对的弦是直径。同弧或等弧所对的圆周角相等；在同圆或等圆中，
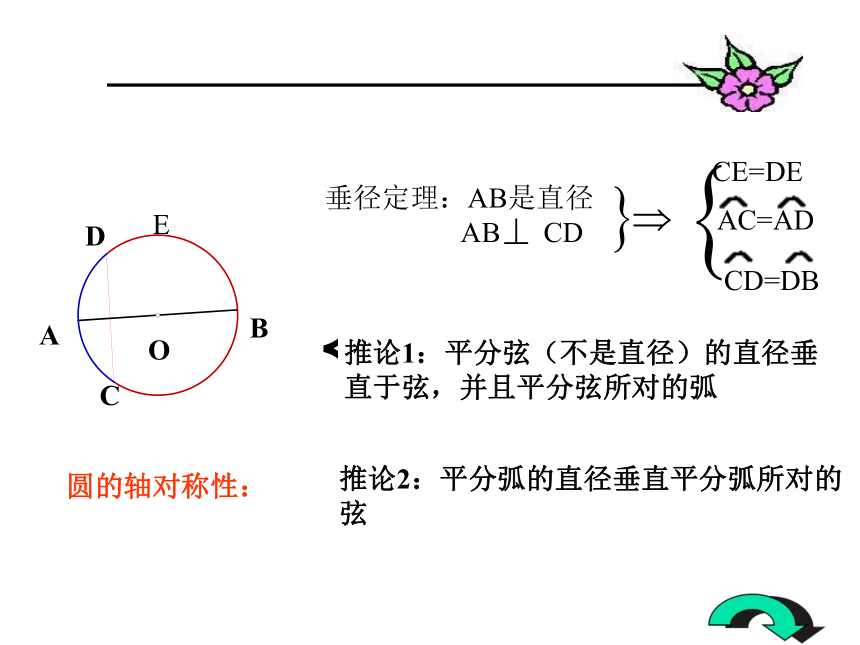
相等的圆周角所对的弧也相等。也可以理解为：一条弧所对的圆心角是它所对的圆周角的二倍；圆周角的度数等于它所对的弧的度数的一半。圆的轴对称性：E垂径定理：AB是直径
AB CD推论1：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的弧推论2：平分弧的直径垂直平分弧所对的弦图1C15例2、如图，P为⊙O的弦BA延长线上一点，PA＝AB＝2，PO＝5，求⊙O的半径。辅助线关于弦的问题，常常需要过圆心作弦的垂线段，这是一条非常重要的辅助线。
圆心到弦的距离、半径、弦长构成直角三角形，便将问题转化为直角三角形的问题。3D3.6做圆的直径与找90度的圆周角也是圆里常用的辅助线例4、半径为５的圆中，有两条平行弦AB 和CD，并且AB =６,CD=８，求AB和CD间的距离.做这类问题是，思考问题一定要全面，考虑到多种情况。例4、半径为５的圆中，有两条平行弦AB 和CD，并且AB 等于６,CD等于８，求AB和CD间的距离. (1)(2)证: 过点O 作OF CD交CD 于 F点,并延长（或反向延长）FO 交AB于 E(如图1、2)，在连接OC、OA，
∴EF=1或7。
有垂径定理得，AE=EB= AB=3CF=FD= CD=4
∵ OF CD，OC=5，CF=4∴OF=3，
∵CD//AB,OF CD∴OE AB，同理：OE=4， ∴EF=OF+OE=4+3=7[图（1）]
EF=OE-OF=4-3=1[图（2）]
练习题1、已知 ⊙ O中，弦AB垂直于直径CD，垂足为P，
AB=6，CP=1，则 ⊙ O的半径为 -------------- 。
2、已知 ⊙ O的直径为10cm,A是⊙ O内一点，且
OA=3cm,则 ⊙ O中过点A的最短弦长=------------- cm 。5850思考题已知AB是⊙ O的直径，弦CD与AB相交，过A，B向CD引垂线，垂足分别为E、F，求证：CE=DF。分析：欲证CE=DF，由于C、D两点是
轴对称点，想到垂径定理，因此过O作
OM CD于M，所以CM=DM，只要证
EM=FM就行了，而AE CD，OM CD，
BF CD，由平行线等分线段定理，可得
M是E、F的中点。O小结1、复习圆的基本性质 2、相关练习谢 谢 观 赏 ！.ABCPO证:∵P为CB的中点引伸1、当BA=AC，∠CAB= 60° ，且当P为CB的中点时，求证：PC=PB= PA∴BP=PC ,BC=PC∵ BA=AC，∠CAB=60°∴ △ABC 是等边三角形, ∠ACB= 60° ∵ ∠APB= ∠ACB(同弧所对的圆周角相等）∴ ∠APB= 60° ∴ △ABP是直角三角形， 又∵ ∠BAP= 30°∴PC=PB= PA
引伸2、正三角形ABC 内接于圆O，P 是CB弧上任意一点，求证：PC+PB= PA. 证法一 证法二D引伸2、正三角形ABC 内接于圆O，P 是CB弧上任意一点，求证：PC+PB= PA∴BD=BP, ∠ CBP=∠ABD证法一:在AP上截取AD=CP,连结BD,
∵△ABC 是等边三角形， ∴AB=BC， ∠ABC= 60°
又∵ BP所对的圆周角为∠PAB，
∠BCP， ∴ ∠PAB =∠BCP
又∵ AD=CP
∴ △ABD≌ △BCP
∴ ∠ DBP=∠ABC= 60°∴ △BPD是正△, ∴BP=PD∴PA=AD+PD=CP+BP引伸2、正三角形ABC 内接于圆O，P 是CB弧上任意一点，求证：PC+PB= PA证法二:D
∴ △ABP≌ △BCD∴AP=CD=DP+PC=BP+PC延长CP至D，使DP=BP,连结BD,
∵ △ABC是等边三角形∴AB=BC，∠BAC= 60°
∵四边形ABPC内接于⊙O，∴∠BPD=∠BAC= 60°
又∵ DP=BP,∠BPD= 60°
∴ △BPD是正△，BP=DP, ∠DBP =60 °∵ ∠DBP= ∠ABC =60 °
∴ ∠ABP= ∠CBD
DD求证两条线段的和常见的辅助线是延长或者截取谢 谢 观 赏 ！