3.1直线与圆的位置关系(2)[上学期]
文档属性
| 名称 | 3.1直线与圆的位置关系(2)[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 147.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-05-23 00:00:00 | ||
图片预览



文档简介
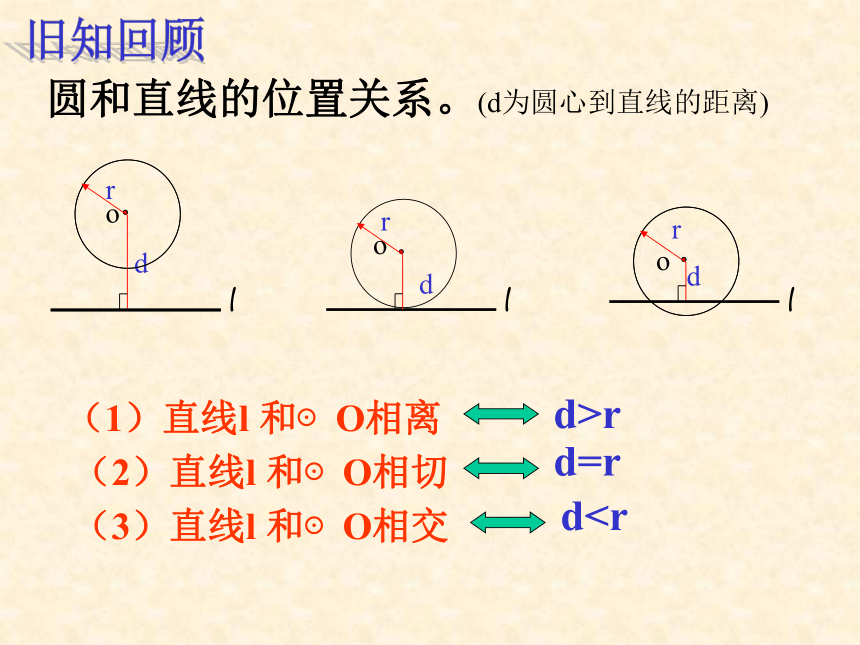
课件13张PPT。3.1 直线与圆的位置关系(2)Hqez wjl321 制作(2)直线l 和⊙O相切圆和直线的位置关系。 (1)直线l 和⊙O相离(3)直线l 和⊙O相交d>rd=rd1.⊙O的半径为3 ,圆心O到直线l的距离为d,若直线l
与⊙O没有公共点,则d为( ):
A.d >3 B.d<3 C.d ≤3 D.d =3
2.圆心O到直线的距离等于⊙O的半径,则直线
和⊙O的位置 关系是( ):
A.相离 B.相交 C.相切 D.相切或相交
3.等边三角形ABC的边长为2,则以A为圆心,半径为1.73的圆
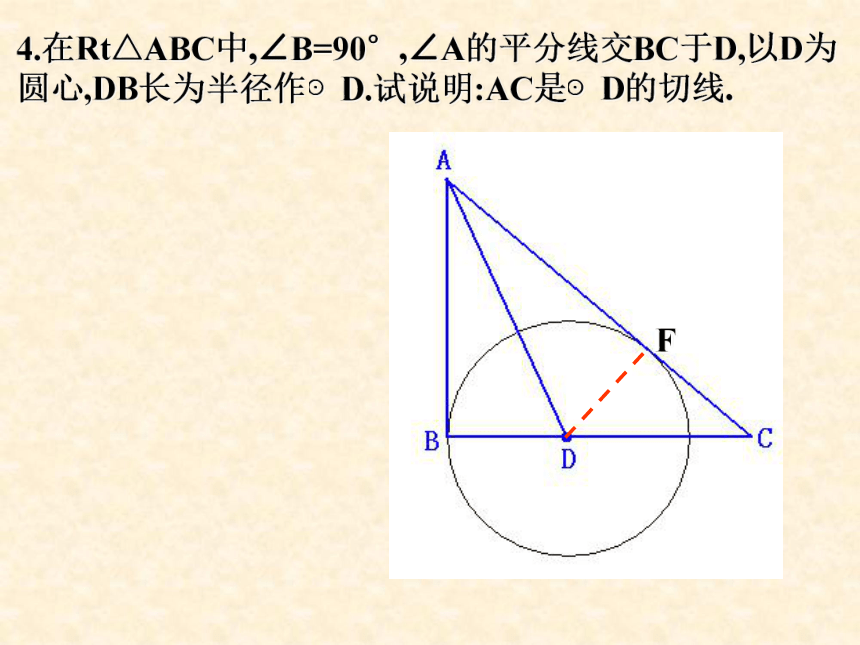
与直线BC的位置关系是 ,以A为圆心,半径为_____ 的圆与直线BC相切.AC相离4.在Rt△ABC中,∠B=90°,∠A的平分线交BC于D,以D为
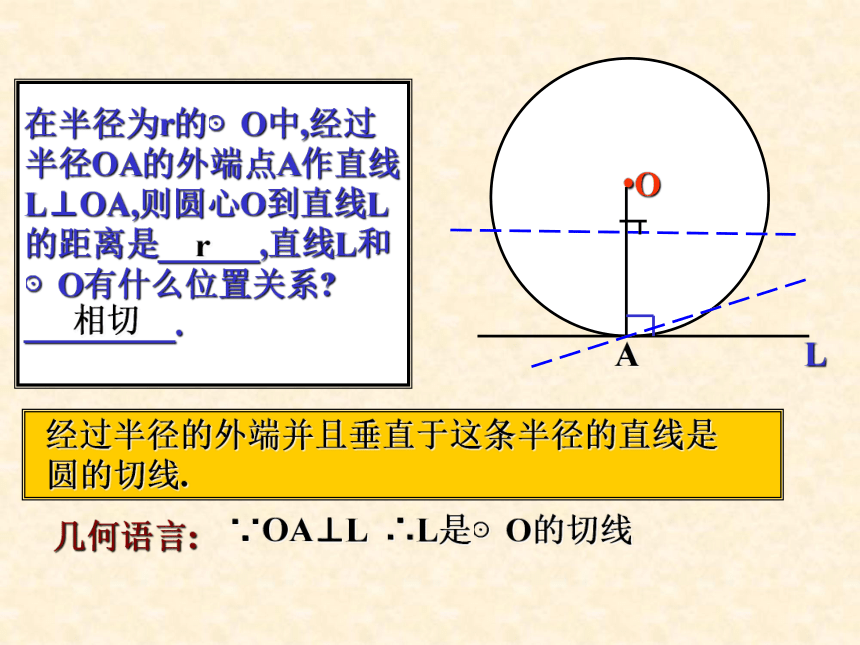
圆心,DB长为半径作⊙D.试说明:AC是⊙D的切线.F在半径为r的⊙O中,经过
半径OA的外端点A作直线
L⊥OA,则圆心O到直线L
的距离是______,直线L和
⊙O有什么位置关系?
_________..OAr相切L经过半径的外端并且垂直于这条半径的直线是
圆的切线.几何语言: ∵OA⊥L ∴L是⊙O的切线(二)切线的判定定理:
1、切线的判定定理:经过半径外端并且垂直于这条半径的直线是圆的切线.2、对定理的理解:切线需满足两条: ①经过半径外端.②垂直于这条半径. 注意:定理中的两个条件缺一不可. 已知一个圆和圆上的一点,如何过这个点画出圆的切线?
oA应用定理.
例1 已知:直线AB经过⊙O上的点C,
并且OA=OB,CA=CB.
求证:直线AB是⊙O的切线. ∴ AB是⊙O的切线. ABCO证明:连结0C∵0A=0B,CA=CB,∴0C是等腰三角形0AB底边AB上的中线.∴AB⊥OC.例2.如图,线段AB经过圆心O,交⊙O于点A,C,∠BAD=∠B=30°,边BD交圆于点D。
求证:BD是⊙O的切线证明:连结OD∵ OA=OD , ∴ OD⊥BD又∵直线BD 经过⊙O上的D点∴直线BD是⊙O的切线∴∠ODA=∠A=300ABCD∴∠BDO=90°∴∠AOD=120°∵ ∠B=30°
证明直线与圆相切有如下方法:1、数量法(d=r):和圆心距离等于半径的直线是
圆的切线。
2、判定定理:经过半径外端且垂直于这条半径的直线是
圆的切线。练习1、如图,AB是⊙O的直径, ∠ABC=45°,
AC=AB,求证AC是⊙O的切线.B.CAO方法小结: 证明过圆上一点的直线是圆的切线.只要证明这条直线垂直于经过切点的半径.2.判断下列命题是否正确.
(1)经过半径外端的直线是圆的切线.( )
(2)垂直于半径的直线是圆的切线.( )
(3)过直径的外端并且垂直于这条直径的直线是圆 的切线.( )
(4)和圆有一个公共点的直线是圆的切线.( )
(5)以等腰三角形的顶点为圆心,底边上的高为半径的圆与底边相切.( )
××√√
√
3.AB是⊙O的直径,AE平分∠BAC交⊙O于点E,过点E
作⊙O的切线交AC于点D,试判断△AED的形状,并
说明理由.
与⊙O没有公共点,则d为( ):
A.d >3 B.d<3 C.d ≤3 D.d =3
2.圆心O到直线的距离等于⊙O的半径,则直线
和⊙O的位置 关系是( ):
A.相离 B.相交 C.相切 D.相切或相交
3.等边三角形ABC的边长为2,则以A为圆心,半径为1.73的圆
与直线BC的位置关系是 ,以A为圆心,半径为_____ 的圆与直线BC相切.AC相离4.在Rt△ABC中,∠B=90°,∠A的平分线交BC于D,以D为
圆心,DB长为半径作⊙D.试说明:AC是⊙D的切线.F在半径为r的⊙O中,经过
半径OA的外端点A作直线
L⊥OA,则圆心O到直线L
的距离是______,直线L和
⊙O有什么位置关系?
_________..OAr相切L经过半径的外端并且垂直于这条半径的直线是
圆的切线.几何语言: ∵OA⊥L ∴L是⊙O的切线(二)切线的判定定理:
1、切线的判定定理:经过半径外端并且垂直于这条半径的直线是圆的切线.2、对定理的理解:切线需满足两条: ①经过半径外端.②垂直于这条半径. 注意:定理中的两个条件缺一不可. 已知一个圆和圆上的一点,如何过这个点画出圆的切线?
oA应用定理.
例1 已知:直线AB经过⊙O上的点C,
并且OA=OB,CA=CB.
求证:直线AB是⊙O的切线. ∴ AB是⊙O的切线. ABCO证明:连结0C∵0A=0B,CA=CB,∴0C是等腰三角形0AB底边AB上的中线.∴AB⊥OC.例2.如图,线段AB经过圆心O,交⊙O于点A,C,∠BAD=∠B=30°,边BD交圆于点D。
求证:BD是⊙O的切线证明:连结OD∵ OA=OD , ∴ OD⊥BD又∵直线BD 经过⊙O上的D点∴直线BD是⊙O的切线∴∠ODA=∠A=300ABCD∴∠BDO=90°∴∠AOD=120°∵ ∠B=30°
证明直线与圆相切有如下方法:1、数量法(d=r):和圆心距离等于半径的直线是
圆的切线。
2、判定定理:经过半径外端且垂直于这条半径的直线是
圆的切线。练习1、如图,AB是⊙O的直径, ∠ABC=45°,
AC=AB,求证AC是⊙O的切线.B.CAO方法小结: 证明过圆上一点的直线是圆的切线.只要证明这条直线垂直于经过切点的半径.2.判断下列命题是否正确.
(1)经过半径外端的直线是圆的切线.( )
(2)垂直于半径的直线是圆的切线.( )
(3)过直径的外端并且垂直于这条直径的直线是圆 的切线.( )
(4)和圆有一个公共点的直线是圆的切线.( )
(5)以等腰三角形的顶点为圆心,底边上的高为半径的圆与底边相切.( )
××√√
√
3.AB是⊙O的直径,AE平分∠BAC交⊙O于点E,过点E
作⊙O的切线交AC于点D,试判断△AED的形状,并
说明理由.
