圆的基本性质复习[上学期]
图片预览

文档简介
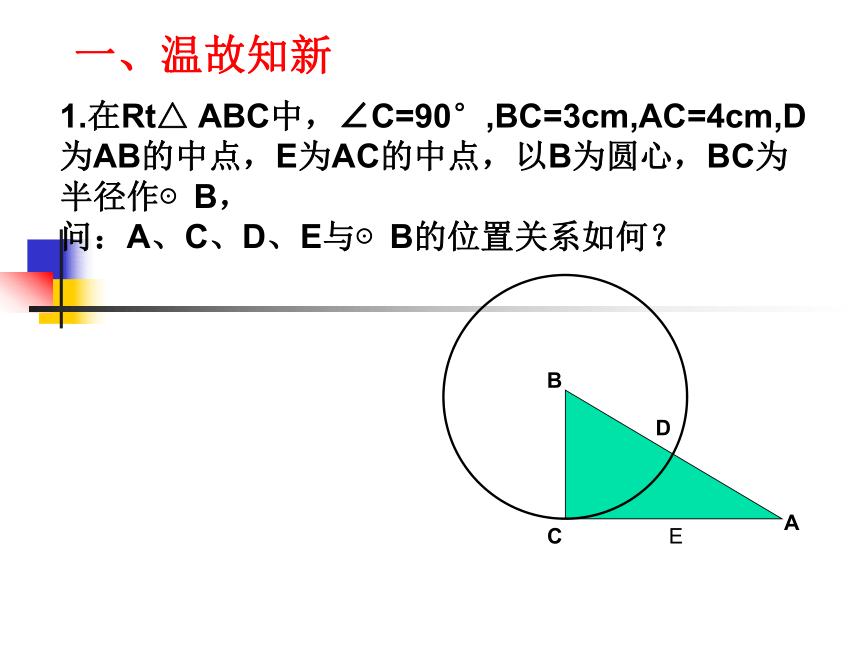
课件16张PPT。圆的基本性质复习1.在Rt△ ABC中,∠C=90°,BC=3cm,AC=4cm,D为AB的中点,E为AC的中点,以B为圆心,BC为半径作⊙B,
问:A、C、D、E与⊙B的位置关系如何?
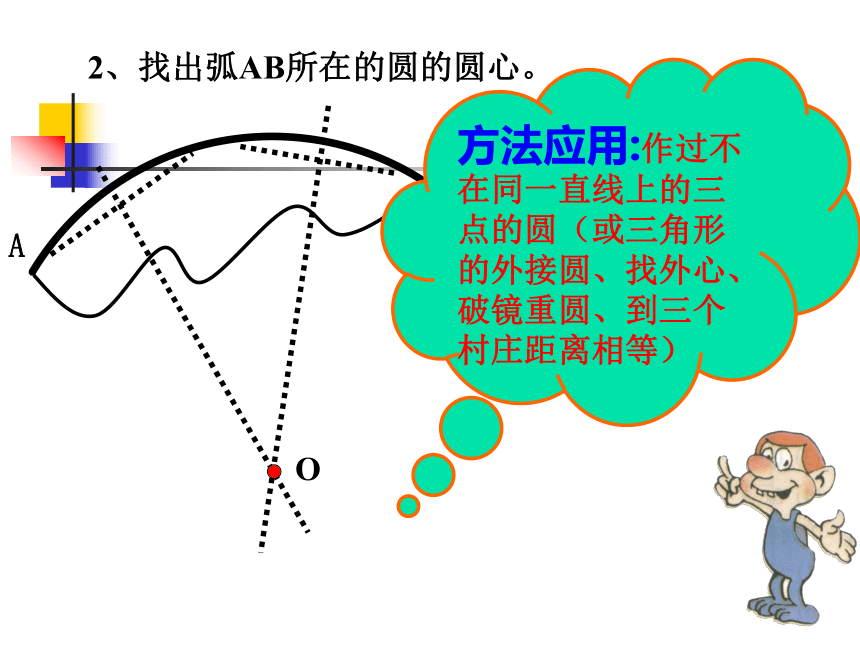
一、温故知新 2、找出弧AB所在的圆的圆心。 OAB方法应用:作过不在同一直线上的三点的圆(或三角形的外接圆、找外心、破镜重圆、到三个村庄距离相等)例1、如图,已知⊙O的半径为r,AB是⊙O的弦。
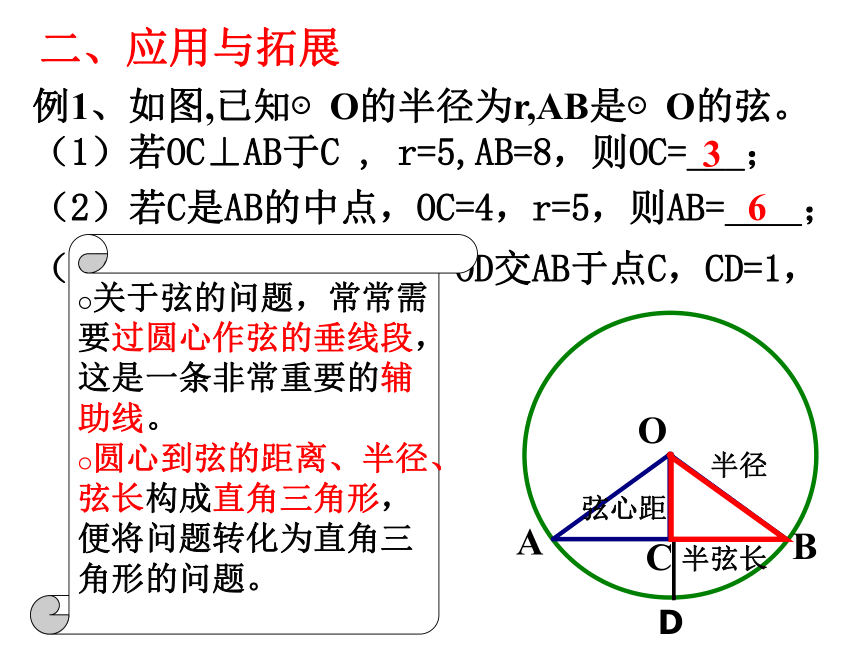
(1)若OC⊥AB于C , r=5,AB=8,则OC=___;3二、应用与拓展(2)若C是AB的中点,OC=4,r=5,则AB= ;(3)若D是弧AB的中点,OD交AB于点C,CD=1,
AB=6,则r = ;66关于弦的问题,常常需要过圆心作弦的垂线段,这是一条非常重要的辅助线。
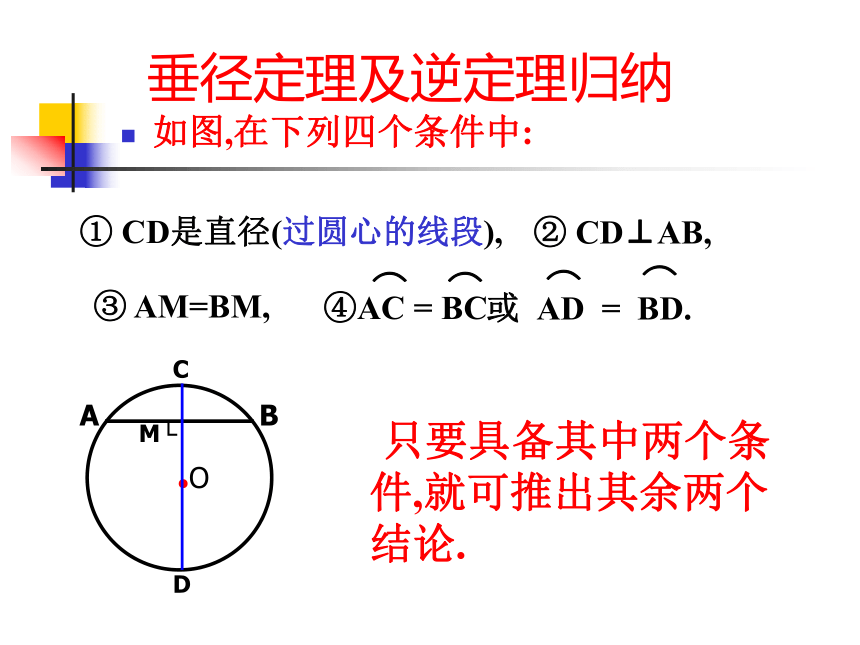
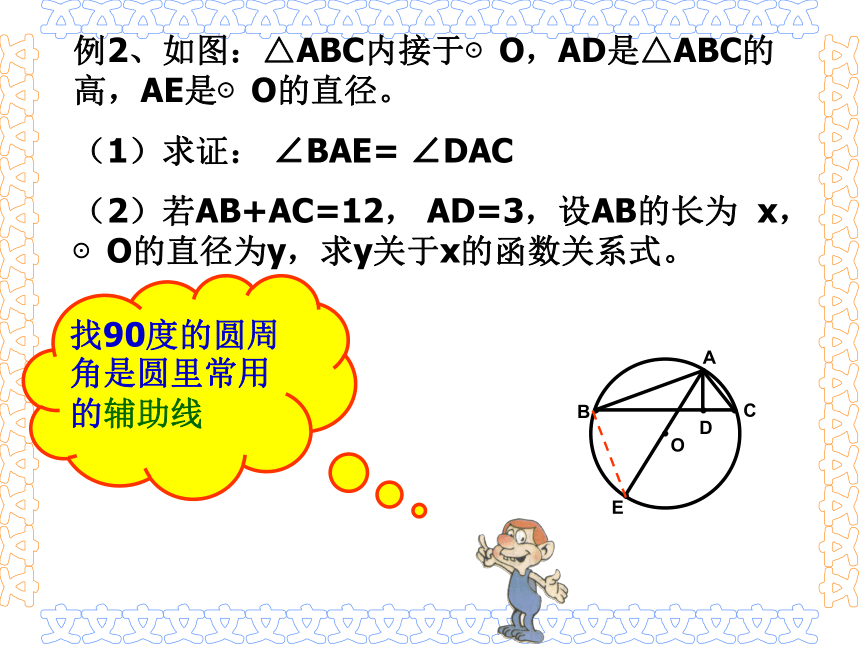
圆心到弦的距离、半径、弦长构成直角三角形,便将问题转化为直角三角形的问题。D垂径定理及逆定理归纳如图,在下列四个条件中: 只要具备其中两个条件,就可推出其余两个结论.① CD是直径(过圆心的线段),③ AM=BM,② CD⊥AB,例2、如图:△ABC内接于⊙O,AD是△ABC的高,AE是⊙O的直径。
(1)求证: ∠BAE= ∠DAC
(2)若AB+AC=12, AD=3,设AB的长为 x, ⊙O的直径为y,求y关于x的函数关系式。找90度的圆周角是圆里常用的辅助线
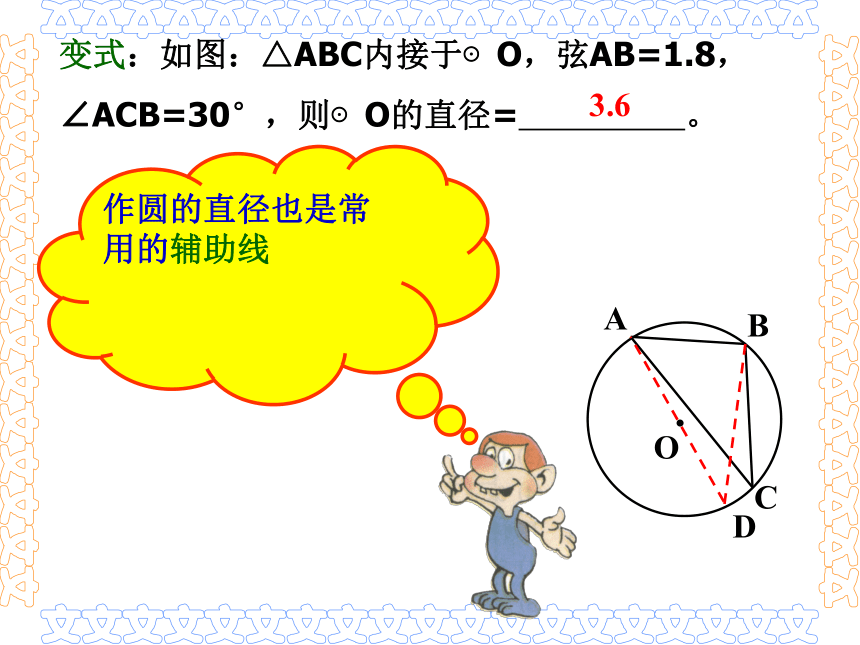
D3.6变式:如图:△ABC内接于⊙O,弦AB=1.8,
∠ACB=30°,则⊙O的直径= 。作圆的直径也是常用的辅助线
例3:AB为⊙O的直径,直线CD交⊙O分别于E、F,AD⊥CD,BC⊥CD垂足分别为D,C。(1)如图(1),当AB∥DC时,请探究:线段DE和CF的大小关系?并说明理由。变式一:若图(1)中的直径AB位置变成图(2)的位置,则(1)中的结论还成立么?试说明理由。变式二:如图(2),若 ⊙O 的半径为5cm,EF=6cm,
DA= 1cm,则DE= cm。1cmDE=CF例3:AB为⊙O的直径,直线CD交⊙O分别于E、F,AD⊥CD,BC⊥CD垂足分别为D,C。变式三:如图,在变式二的基础上,以DC为X轴,DA为Y轴建立直角坐标系。求过点A、 E 、F的抛物线所对应的函数解析式。变式二:如图(2),若 ⊙O 的半径为5cm,EF=6cm,
DA= 1cm,则DE= cm。1cm思考题如图① ,△ABC(AB>AC)内接于⊙O,若直线AD平分∠BAC交BC于点D,交⊙O于点E。
(1)求证:AB·AC=AD·AE。图①(2)若把题中的条件“直线AD平分∠BAC”改为“直线AD平分∠BAC的外角”如图② ,那么(1)中结论是否仍然成立?请说明理由。图②这节课我们复习了哪些知识?
你有什么收获?
还有哪些疑惑?小结祝同学们学习进步
再 见1、已知 ⊙ O中,弦AB垂直于直径CD,垂足为P,
AB=6,CP=1,则 ⊙ O的半径为 -------------- 。2、已知 ⊙ O的直径为10cm,A是⊙ O内一点,且OA=3cm,则 ⊙ O中过点A的最短弦长=------------- cm 。 58练一练 3、在⊙O中,弦AB所对的圆心角∠AOB=100°,则弦AB所对的圆周角为____________.50°或130°图(1)图(2)4、如图, 点A、B、C是圆O上的三点,AB=500, ∠OBC=400,则∠OAC的度数是 。OBCA1505、锐角三角形的外心在三角形 ,
直角三角形的外心在三角形 ,
钝角三角形的外心在三角形 。6、半径为5的圆中,有两条平行弦AB 和CD,并且AB =6,CD=8,求AB和CD间的距离为 。做这类问题是,思考问题一定要全面,考虑到多种情况。1、某地有一座圆弧形的拱桥,桥下的水面宽为7.2m,拱顶高出水面2.4m,?Or=3.9 m思考题
问:A、C、D、E与⊙B的位置关系如何?
一、温故知新 2、找出弧AB所在的圆的圆心。 OAB方法应用:作过不在同一直线上的三点的圆(或三角形的外接圆、找外心、破镜重圆、到三个村庄距离相等)例1、如图,已知⊙O的半径为r,AB是⊙O的弦。
(1)若OC⊥AB于C , r=5,AB=8,则OC=___;3二、应用与拓展(2)若C是AB的中点,OC=4,r=5,则AB= ;(3)若D是弧AB的中点,OD交AB于点C,CD=1,
AB=6,则r = ;66关于弦的问题,常常需要过圆心作弦的垂线段,这是一条非常重要的辅助线。
圆心到弦的距离、半径、弦长构成直角三角形,便将问题转化为直角三角形的问题。D垂径定理及逆定理归纳如图,在下列四个条件中: 只要具备其中两个条件,就可推出其余两个结论.① CD是直径(过圆心的线段),③ AM=BM,② CD⊥AB,例2、如图:△ABC内接于⊙O,AD是△ABC的高,AE是⊙O的直径。
(1)求证: ∠BAE= ∠DAC
(2)若AB+AC=12, AD=3,设AB的长为 x, ⊙O的直径为y,求y关于x的函数关系式。找90度的圆周角是圆里常用的辅助线
D3.6变式:如图:△ABC内接于⊙O,弦AB=1.8,
∠ACB=30°,则⊙O的直径= 。作圆的直径也是常用的辅助线
例3:AB为⊙O的直径,直线CD交⊙O分别于E、F,AD⊥CD,BC⊥CD垂足分别为D,C。(1)如图(1),当AB∥DC时,请探究:线段DE和CF的大小关系?并说明理由。变式一:若图(1)中的直径AB位置变成图(2)的位置,则(1)中的结论还成立么?试说明理由。变式二:如图(2),若 ⊙O 的半径为5cm,EF=6cm,
DA= 1cm,则DE= cm。1cmDE=CF例3:AB为⊙O的直径,直线CD交⊙O分别于E、F,AD⊥CD,BC⊥CD垂足分别为D,C。变式三:如图,在变式二的基础上,以DC为X轴,DA为Y轴建立直角坐标系。求过点A、 E 、F的抛物线所对应的函数解析式。变式二:如图(2),若 ⊙O 的半径为5cm,EF=6cm,
DA= 1cm,则DE= cm。1cm思考题如图① ,△ABC(AB>AC)内接于⊙O,若直线AD平分∠BAC交BC于点D,交⊙O于点E。
(1)求证:AB·AC=AD·AE。图①(2)若把题中的条件“直线AD平分∠BAC”改为“直线AD平分∠BAC的外角”如图② ,那么(1)中结论是否仍然成立?请说明理由。图②这节课我们复习了哪些知识?
你有什么收获?
还有哪些疑惑?小结祝同学们学习进步
再 见1、已知 ⊙ O中,弦AB垂直于直径CD,垂足为P,
AB=6,CP=1,则 ⊙ O的半径为 -------------- 。2、已知 ⊙ O的直径为10cm,A是⊙ O内一点,且OA=3cm,则 ⊙ O中过点A的最短弦长=------------- cm 。 58练一练 3、在⊙O中,弦AB所对的圆心角∠AOB=100°,则弦AB所对的圆周角为____________.50°或130°图(1)图(2)4、如图, 点A、B、C是圆O上的三点,AB=500, ∠OBC=400,则∠OAC的度数是 。OBCA1505、锐角三角形的外心在三角形 ,
直角三角形的外心在三角形 ,
钝角三角形的外心在三角形 。6、半径为5的圆中,有两条平行弦AB 和CD,并且AB =6,CD=8,求AB和CD间的距离为 。做这类问题是,思考问题一定要全面,考虑到多种情况。1、某地有一座圆弧形的拱桥,桥下的水面宽为7.2m,拱顶高出水面2.4m,?Or=3.9 m思考题
同课章节目录
